Βοήθεια/Απορίες στην Άλγεβρα

Dimitris0mg · 02-05-09

μαγκας ευχαριστω...

papas · 02-05-09

Στον πολλαπλασιασμο υπαρχει μια διαφορα:Θα κανεις τον πολλαπλασιασμο κλασματων,ομως ο αριθμιτης θα σου βγει διαφορα τετραγωνων και την Δ θα πρεπει να την γραφεις β^2-4αγ για να προχωρησεις μετα.

tebelis13 · 03-05-09

ο thewatcher σιγουρα βγαζει 13.4 ?

Iliaso · 03-05-09

:s:s:s:s:s πρέπει να το πάρω απόφαση

...

Civilara · 03-05-09

a+b=40 -> b=40-a
ab=a(40-a)=-(a^2)+40a=f(a)
f΄(a)=-2a+40
f΄΄(a)=-2
f΄(a)=0 -> -2a+40=0 -> a=20
f΄(20)=0, f΄΄(20)=-2<0 -> μέγιστο για a=20 -> b=40-a=20
max(ab)=f(20)=-(20^2)+40*20=400

thewatcher · 03-05-09

Παιδιά, μην απογοητεύεστε, η άσκηση ήταν πολύ δύσκολη και σε καμία περίπτωση σχολική

(μιλάω για αυτή που έδωσε ο p@g, η άλλη ήταν πιο εύκολη)

Dreamkiller · 03-05-09

Έχω την εντύπωση ότι η άσκηση είναι λάθος.
Για $a = b = c = \frac{1}{3}$ παίρνουμε ότι

$\frac {1}{3} \geq \frac {1}{2} - 2 \frac {1}{27} \leftrightarrow \frac {18}{54} \geq \frac {27}{54} - \frac {4}{54} \leftrightarrow \frac {18}{54} \geq \frac {23}{54}$ , που προφανώς δεν ισχύει.
Πάντως και στον Ευκλείδη Β' το περιοδικό έτσι την έχουν δώσει.

mariavrdf · 04-05-09

α+β=40 <=> β=40-α
Εστω Π(χ)=α*β = α*(40-α) = 40α-α^2
π'(χ)=40-2α π(χ)=0 <=> 40=2α <=> α=20
αρα β=20 και η μεγιστη τιμη ειναι α*β=400
και με πινακα βγαινει η π' στο πρωτο διαστημα + οποτε η π γνησιως αυξουσα και στο αλλο - οποτε η π ειναι φθινουσα οποτε οντως εχουμε μεγιστη τιμη
πιανεται ετσι η λυση?

joseph · 04-05-09

Η ανισότητα Cauchy-Schwarz έχει διάφορες "μορφές" και εξαρτάται από ποιο "χώρο" δουλεύουμε, μια μικρή αναφορά είναι στην ακόλουθη address https://en.wikipedia.org/wiki/Cauchy-Schwarz_inequality. Στο βιβλίο υπάρχουν κάποιες αποδεικτικές ασκήσεις που ουσιαστικά είναι ειδικές περιπτώσεις της ανισότητας.
Η ισότητα Euler υπάρχει ως παράδειγμα λυμένο στο σχολικό βιβλίο της Άλγεβρας της Α΄Λυκείου σελίδα 19 παράδειγμα 3i.
Αναφορικά υπάρχει και μία άλλη ισότητα που είναι άσκηση του βιβλίου της Άλγεβρας της Α΄Λυκείου σελίδα 22 Άσκηση 4i, που ονομάζεται ταυτότητα Lagrande.

djimmakos · 04-05-09

Αρχική Δημοσίευση από mariavrdf:
α+β=40 <=> β=40-α
Εστω Π(χ)=α*β = α*(40-α) = 40α-α^2
π'(χ)=40-2α π(χ)=0 <=> 40=2α <=> α=20
αρα β=20 και η μεγιστη τιμη ειναι α*β=400
και με πινακα βγαινει η π' στο πρωτο διαστημα + οποτε η π γνησιως αυξουσα και στο αλλο - οποτε η π ειναι φθινουσα οποτε οντως εχουμε μεγιστη τιμη
πιανεται ετσι η λυση?

Στην A λυκείου δεν κάνουμε παραγωγους

thewatcher · 04-05-09

Αρχική Δημοσίευση από Dreamkiller:
Έχω την εντύπωση ότι η άσκηση είναι λάθος.
Για $a = b = c = frac{1}{3}$ παίρνουμε ότι

$frac {1}{3} geq frac {1}{2} - 2 frac {1}{27} leftrightarrow frac {18}{54} geq frac {27}{54} - frac {4}{54} leftrightarrow frac {18}{54} geq frac {23}{54}$ , που προφανώς δεν ισχύει.
Πάντως και στον Ευκλείδη Β' το περιοδικό έτσι την έχουν δώσει.

Έλεος τι καθόμασταν και ψάχναμε τόσο καιρο :s

darkn1ck · 10-05-09

Αρχική Δημοσίευση από Djimmakos:
Ε ναι, σίγουρα με βοήθησε και το γεγονός ότι είδα και τη δικιά σου λύση πρώτα

Eξάλλου δεν είπα πουθενά ότι τη βρήκα μόνος μου, απλώς μια λύση έγραψα

Jimmy μαθηματικό θα πάς?

SuXu-MuXu · 10-05-09

Ξέρω ότι το θέμα είναι αρκετά παλιό αλλά επειδή ήταν πολύ ενδιαφέρον με αρκετές ωραίες ασκήσεις το επαναφέρω στις πρώτες σελίδες. Καλό θα ήταν όποιος έχει κάποια καλή άσκηση να την βάζει έτσι ώστε να το κράτησουμε ως θέμα ενεργό και να μην το αφήσουμε να ξαναγυρίσει στα «αζήτητα».

Με την ευκαιρία θα ήθελα να χαιρετίσω όλους τους ischoolήτες. Παρακολουθώ το forum αρκετό καιρό και επιτέλους αποφάσισα να γίνω και εγώ μέλος. Καλώς με βρήκατε!

djimmakos · 11 Ιουλίου 2012

Αρχική Δημοσίευση από darkn1ck:
Jimmy μαθηματικό θα πάς?

Μπα.

Προτιμώ να σπουδάσω κάτι που να περιέχει μαθηματικά από τα να σπουδάσω μόνο μαθηματικά.

Aς βάλω εγώ μια επαναληπτική.

Αν $x \in (-3,1)$ να δείξετε ότι

$|-x^2+2x-3|<18$

Εγώ έχω βρει δύο τρόπους μέχρι τώρα. Ψάχνω και τρίτο

-----------------------------------------

Αρχική Δημοσίευση από Hurr:
Ασκηση 2
Να απλοποιηθεί η παράσταση:
$sqrt{13+30sqrt{2+sqrt{9+4sqrt{2}}}}$

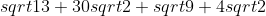
Aν και λιγο αργοπορημένα. (Tώρα την είδα)

$\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}=\sqrt{13+30\sqrt{2+\sqrt{(2\sqrt{2})^2+1+2\cdot 2\sqrt{2}}}}=\sqrt{13+30\sqrt{2+\sqrt{(2\sqrt{2}+1)^2}}}=\sqrt{13+30\sqrt{2+1+2\sqrt{2}}}= \sqrt{13+30\sqrt{(\sqrt{2}+1)^2}}}=\sqrt{13+30(1+ \sqrt{2})}=\sqrt{13+30+30\sqrt{2}}$

Ελπίζω να μην έχω κάνει κάποιο λάθος γιατί με τόσες ρίζες...

Τελικά το έκανα το λαθάκι και στο τέλος αντί για πολλαπλασιασμό έκανα πρόσθεση. Το διορθώνωωωω.

To διόρθωσα

Τώρα για να διώξουμε και την τελευταία ρίζα πρέπει να κάνουμε την υπόρριζη πόσοτητα τέλειο τετράγωνο βρίσκοντας τέτοιους αριθμούς έτσι ώστε:
$a^2+b^2=43$ και $ab=15\sqrt{2}$ .

Aιτιολόγηση:
Θέλουμε $43+30\sqrt{2}=(a+b)^2=a^2+b^2+2ab$ και από τη θεωρία αριθμών το άρρητο μέρος του πρώτου μέλους θα ισούται με το άρρητο μέρος του δεύτερου μέλους ( $2ab=30\sqrt{2}$ ). Το ίδιο ισχύει και για τα ρητά μέρη των δύο μελών.

SuXu-MuXu · 11-05-09

Αρχική Δημοσίευση από Djimmakos:
Τώρα για να διώξουμε και την τελευταία ρίζα πρέπει να κάνουμε την υπόρριζη πόσοτητα τέλειο τετράγωνο βρίσκοντας τέτοιους αριθμούς έτσι ώστε:
$a^2+b^2=43$ και $ab=15sqrt{2}$ .

Aιτιολόγηση:
Θέλουμε $43+30sqrt{2}=(a+b)^2=a^2+b^2+2ab$ και από τη θεωρία αριθμών το άρρητο μέρος του πρώτου μέλους θα ισούται με το άρρητο μέρος του δεύτερου μέλους ( $2ab=30sqrt{2}$ ). Το ίδιο ισχύει και για τα ρητά μέρη των δύο μελών.

Και εγώ την είχα προσπαθήσει αυτην αλλα καταφερα να την φτάσω μέχρι την τελεταία ρίζα.

Για την θεωρία των αριθμών τώρα, ξέρεις μήπως που μπορώ να βρώ στο internet κάποιο e-book η κάποιο άρθρο έτσι ώστε να μάθω καποια πράγματα; Εχω προσπαθήσει να βρώ αλλά δεν κατάφερα να βρώ κατι που να αρχίζει απο τα βασικά.

papas · 11-05-09

Αρχική Δημοσίευση από SuXu-MuXu:
Και εγώ την είχα προσπαθήσει αυτην αλλα καταφερα να την φτάσω μέχρι την τελεταία ρίζα.

Για την θεωρία των αριθμών τώρα, ξέρεις μήπως που μπορώ να βρώ στο internet κάποιο e-book η κάποιο άρθρο έτσι ώστε να μάθω καποια πράγματα; Εχω προσπαθήσει να βρώ αλλά δεν κατάφερα να βρώ κατι που να αρχίζει απο τα βασικά.

Αμα εχεις καποιο βιβλιοπωλειο Παπασωτηριου κοντα σου,στο τμημα με τα Μαθηματικα πουλανε και βιβλια με θεωρια αριθμων

SuXu-MuXu · 11-05-09

Είμαι απο ρόδο και δεν πρέπει να υπάρχει τετοιο βιβλιοπωλείο. Ξερεις μηπως κανένα συγκεκριμένο βιβλιο. κατάλληλο για Α λυκείου, αν είναι να το ψάξω σε κάποιο άλλο βιβλιοπωλείο. Πάντως η λύση του ιντερνετ είναι πιστευω καλύτερη για μια πρώτη φάση, αν ξέρει κάποιος κανένα site.
-----------------------------------------

Αρχική Δημοσίευση από Djimmakos:
Aς βάλω εγώ μια επαναληπτική.

Αν $x in (-3,1)$ να δείξετε ότι
$|-x^2+2x-3|<18$

$\left|-x^2+2x-3 \right|< 18 \Leftrightarrow -18<-x^2+2x-3<21 \Leftrightarrow -15<-x^2+2x<24 \Rightarrow -x^2+2x+15>0$ και $-x^2+2x-24<0$
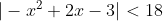
Το πρώτο έχει λύσεις τις -3,5 έτσι παίρνουμε $x\in \left(-3,5 \right)$
Για το δεύτερο μας βγαίνει Δ<0 οπότε το τριώνυμο είναι αρνητικό για κάθε τιμή του x
Από αυτές τις παίρνουμε πως η (1) αληθεύει για $x\in \left(-3,5 \right)$
Επειδή τώρα το (-3,5) περιέχει το (-3,1) αποδεικνύεται πως ισχύει αυτό που ψάχναμε.

Αχχχ αυτο το LaTeX....

Papas έχεις δίκιο, λάθος μου στις πράξεις, ευτυχώς όμως δεν επηρεάζει το αποτέλεσμα.
Ευχαριστο και για το αρθρο της ΕΜΕ έχει αρκετά πράγματα!

papas · 11-05-09

Χμ...γτ το τριωνυμο να ειναι μικροτερο του 21,αφου |x|<0 <=> -θ<x<θ?(Ξερω οτι αφαιρεσες το -3 απο το τριωνυμο,αλλα και παλι στην αρχη θα επρεπε να ειχες κανει συγχρονως και για το -18 και για το 18 τις προσθαφαιρεσεις

)

Επισης,για την θεωρια αριθμο που ζητησες,πατα εδω.

p@g · 11-05-09

Βάζω και γω μια αρκετα ευκολη απλα για να μην ξεχνιομαστε.εστω
$f:R\rightarrow R$ και $f({x}_{1}+{x}_{2})=f({x}_{1})+f({x}_{2})$ για καθε ${x}_{1},{x}_{2} \epsilon R$ ν.δ.ο $f(0)=0$

djimmakos · 11-05-09

Αρχική Δημοσίευση από p@g:
Βάζω και γω μια αρκετα ευκολη απλα για να μην ξεχνιομαστε.εστω
$f:Rrightarrow R$ και $f({x}_{1}+{x}_{2})=f({x}_{1})+f({x}_{2})$ για καθε ${x}_{1},{x}_{2} epsilon R$ ν.δ.ο $f(x)=0$

Όταν λες f(x)=0, ουσιαστικά μιλάς για τον άξονα των χ (ό,τι τιμή και να πάρει το x, το y θα είναι μηδέν).

Την ιδιότητα αυτή την έχουν και άλλες συναρτήσεις όμως.

Μήπως θες να πεις f(0)=0;

Βοήθεια/Απορίες στην Άλγεβρα

Νεοφερμένος

Διάσημο μέλος

Πολύ δραστήριο μέλος

Περιβόητο μέλος

Περιβόητο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Νεοφερμένος

Νεοφερμένος

Διάσημο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Διάσημο μέλος

Εκκολαπτόμενο μέλος

Διάσημο μέλος

Εκκολαπτόμενο μέλος

Διάσημο μέλος

Εκκολαπτόμενο μέλος

Διάσημο μέλος