Βοήθεια/Απορίες στα Μαθηματικά Προσανατολισμού - Ασκήσεις

antwwwnis · 10-05-11

Εγω εχω μια αλλη απορια.
λεει η ασκηση: Δινονται σημεια Β(-2,3) και Γ(4,5)
Να βρεθει ο Γτ των σημειων Α ωστε ΑΒ/ΑΓ=λ, οπου λ πραγματικος θετικος διαφορος του μηδενος.
Εγω την πηγα ετσι την ασκηση:

Η παραπανω προταση ειναι ισοδυναμη με την ΑΒ/ΑΓ>0 (πραξεις) που ισχυει για ολο το επιπεδο εκτος των σημειων Β και Γ.
Επομενως Α ανηκει στο R² ' (B, Γ)

Ειναι σωστο; Γιατι η λυση ελεγε κατι για κυκλους και 2,5 σελιδες πραξεις....

antonio2761994 · 10-05-11

Αρχική Δημοσίευση από styt_geia:
Μια προφανής είναι η χ=0. Απο κει και πέρα προσπαθώντας να βρω εφαπτομένες της μορφής y=lx+b κατέληξα στις εξισώσεις
$4lb=1 (1) \quad -4 (-2 b + b^2 - 2 l + 2 b l)=0 (2)$

το σύστημα των οποίων όμως δεν κατάφερα να λύσω στο χέρι αλλά με την βοήθεια υπολογιστή

Τελικά βρήκα $l\approx 0,133$ και $b\approx 1,876$

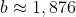
φίλε εκεί είχα φτάσει κι εγώ.. και όντως σήμερα μας είπε ο καθηγητής ότι δεν βγαίνει κάτι. απλά ήθελε να δει ποιος θα σεκφτόταν να προσδιορίσει τη ρίζα

rebel · 11-05-11

Αρχική Δημοσίευση από antwwwnis:
Εγω εχω μια αλλη απορια.
λεει η ασκηση: Δινονται σημεια Β(-2,3) και Γ(4,5)
Να βρεθει ο Γτ των σημειων Α ωστε ΑΒ/ΑΓ=λ, οπου λ πραγματικος θετικος διαφορος του μηδενος.
Εγω την πηγα ετσι την ασκηση:

Η παραπανω προταση ειναι ισοδυναμη με την ΑΒ/ΑΓ>0 (πραξεις) που ισχυει για ολο το επιπεδο εκτος των σημειων Β και Γ.
Επομενως Α ανηκει στο R² ' (B, Γ)

Ειναι σωστο; Γιατι η λυση ελεγε κατι για κυκλους και 2,5 σελιδες πραξεις....

Κάθε σημείο Α(χ,y) του γ.τ. θα πρέπει να ικανοποιεί την $AB^2=\lambda^2 A\Gamma^2$ και όχι αυτή που γράφεις. Μετά από επίπονες πράξεις τελικά καταλήγεις ότι για λ=1 παριστάνει ευθεία, ενώ για $\lambda \neq 1$ κύκλο.

antwwwnis · 11-05-11

Αρχική Δημοσίευση από styt_geia:
Κάθε σημείο Α(χ,y) του γ.τ. θα πρέπει να ικανοποιεί την $AB^2=\lambda^2 A\Gamma^2$ και όχι αυτή που γράφεις. Μετά από επίπονες πράξεις τελικά καταλήγεις ότι για λ=1 παριστάνει ευθεία, ενώ για $\lambda \neq 1$ κύκλο.

Aααα, δηλαδη δεν ειναι το ιδιο ε?
Το λεω γιατι στην τελικη σημεια ψαχνουμε, και φαινεται πως μας κανουν ολα εκτος απο το B που μηδενιζει το πηλικο και το Γ που μηδενιζει παρωνομαστη.
Συγγνωμη που επιμενω αλλα θελω να καταλαβω την ασκηση, καλα!

jjoohhnn · 11-05-11

Antwwwni από το oktonia δεν είναι η άσκηση?

rebel · 11-05-11

Τώρα κατάλαβα τι ακριβώς θες να πεις. Εννοείς πως αν αφήσουμε το λ να τρέχει στο $(0,+\infty)$ , τότε για κάθε σημείο Α του επιπέδου εκτός από τα Β και Γ θα υπάρχει κάποιο λ>0 για το οποίο το Α θα ανήκει στον γεωμετρικό τόπο. Σε αυτό έχεις δίκιο.
Όμως το λ θεωρείται σταθερό. Απλως για κάθε λ παράγεται και διαφορετικός γ.τ. . Στο παρακάτω σχήμα φαίνεται ότι για λ=1 ο γ.τ. είναι μια ευθεία και συγκεκριμένα η (ε): y=-3x+7. Για λ<1 όπως βλέπεις, ο γεωμετρικός τόπος είναι ένας κύκλος που έχει το κέντρο του στο αριστερό ημιεπίπεδο που ορίζει η (ε) ενώ για λ>1 είναι πάλι ένας κύκλος που έχει το κέντρο του στο δεξί ημιεπίπεδο.

antwwwnis · 11-05-11

Αρχική Δημοσίευση από styt_geia:
Τώρα κατάλαβα τι ακριβώς θες να πεις. Εννοείς πως αν αφήσουμε το λ να τρέχει στο $(0,+\infty)$ , τότε για κάθε σημείο Α του επιπέδου εκτός από τα Β και Γ θα υπάρχει κάποιο λ>0 για το οποίο το Α θα ανήκει στον γεωμετρικό τόπο. Σε αυτό έχεις δίκιο.
Όμως το λ θεωρείται σταθερό. Απλως για κάθε λ παράγεται και διαφορετικός γ.τ. . Στο παρακάτω σχήμα φαίνεται ότι για λ=1 ο γ.τ. είναι μια ευθεία και συγκεκριμένα η (ε): y=-3x+7. Για λ<1 όπως βλέπεις, ο γεωμετρικός τόπος είναι ένας κύκλος που έχει το κέντρο του στο αριστερό ημιεπίπεδο που ορίζει η (ε) ενώ για λ>1 είναι πάλι ένας κύκλος που έχει το κέντρο του στο δεξί ημιεπίπεδο.

Ναι ακριβως αυτο εννοουσα!
Δηλαδη αν εδινα απαντηση αυτο που ειπα, θεωρειται λαθος?
Εχω λυσει ασκησεις που κανω διερευνηση, ωστε να βρω τι παριστανει μια εξισωση με παραμετρο στο επιπεδο.
Αλλα με γεωμετρικους τοπους συνηθως βρισκω ποια σημεια ταιριαζουν.
Ωραιο προγραμμα!

Antwwwni από το oktonia δεν είναι η άσκηση?

Ναι, εχει πολυ καλες ασκησεις εκει.

rebel · 11 Μαΐου 2011

Ναι είναι λάθος. Θα πρέπει στην απάντησή σου να πεις ότι για λ=1 ο γ.τ. είναι η ευθεία τάδε ενώ για λ διάφορο του 1 είναι ο κύκλος με κέντρο τάδε και ακτίνα τάδε (προφανώς οι συντεταγμένες του κέντρου αλλά και η ακτίνα θα είναι συναρτήσεις του λ). Κάτι που δεν παρατήρησα και το είδα στην λύση που δίνει στο oktonia είναι ότι τα κέντρα των κύκλων κινούνται πάνω στην ευθεία ΒΓ. Σωστό και αυτό!

antwwwnis · 11-05-11

Αρχική Δημοσίευση από styt_geia:
Ναι είναι λάθος. Θα πρέπει στην απάντησή σου να πεις ότι για λ=1 ο γ.τ. είναι η ευθεία τάδε ενώ για λ διάφορο του 1 είναι ο κύκλος με κέντρο τάδε και ακτίνα τάδε (προφανώς οι συντεταγμένες του κέντρου αλλά και η ακτίνα θα είναι συναρτήσεις του λ). Κάτι που δεν παρατήρησα και το είδα στην λύση που δίνει στο oktonia είναι ότι τα κέντρα των κύκλων κινούνται πάνω στην ευθεία ΒΓ. Σωστό και αυτό!

Eυχαριστω πολυ! :thumbsup:

Αυτο πρεπει να το εχω υποψιν μου.

Rempeskes · 13-05-11

Αρχική Δημοσίευση από styt_geia:
Τώρα κατάλαβα τι ακριβώς θες να πεις. Εννοείς πως αν αφήσουμε το λ να τρέχει στο $(0,+\infty)$ , τότε για κάθε σημείο Α του επιπέδου εκτός από τα Β και Γ θα υπάρχει κάποιο λ>0 για το οποίο το Α θα ανήκει στον γεωμετρικό τόπο. Σε αυτό έχεις δίκιο.
Όμως το λ θεωρείται σταθερό. Απλως για κάθε λ παράγεται και διαφορετικός γ.τ. . Στο παρακάτω σχήμα φαίνεται ότι για λ=1 ο γ.τ. είναι μια ευθεία και συγκεκριμένα η (ε): y=-3x+7. Για λ<1 όπως βλέπεις, ο γεωμετρικός τόπος είναι ένας κύκλος που έχει το κέντρο του στο αριστερό ημιεπίπεδο που ορίζει η (ε) ενώ για λ>1 είναι πάλι ένας κύκλος που έχει το κέντρο του στο δεξί ημιεπίπεδο.

Aχ, τι υπέροχο πράγμα τα παλιά βιβλία...
Αυτός ο γεωμετρικός τόπος χαρακτηρίζεται ως "δέσμη κωνικών τομών".

antwwwnis · 13-05-11

Αρχική Δημοσίευση από Rempeskes:
Aχ, τι υπέροχο πράγμα τα παλιά βιβλία...
Αυτός ο γεωμετρικός τόπος χαρακτηρίζεται ως "δέσμη κωνικών τομών".

Κι εμενα μου αρεσουν. Στις εξετασεις επεσε οικογενεια κυκλων, η C(λ): (χ-λ)²+(y-λ+1)²=λ², λ€R*

debbie · 8 Σεπτεμβρίου 2011

παρακολουθώ μαθηματικά κατευθύνσεις και έχω κάτι ασκήσεις αλλα δεν μπορώ να λύσω αυτό το είδος...please help
1. $\frac{|x|-1}{|x|-2}$ (είναι σε κλάσμα ή δείχνει το κλάσμα)
2. $\frac{x}{1-|x|}$
3. $\frac{x}{|x|+1}$
4. $\frac{|x+1|}{|x-1|+2}$

Andreas12 · 8 Σεπτεμβρίου 2011

Αρχική Δημοσίευση από debbie:
παρακολουθώ μαθηματικά κατευθύνσεις και έχω κάτι ασκήσεις αλλα δεν μπορώ να λύσω αυτό το είδος...please help
1.

(είναι σε κλάσμα ή δείχνει το κλάσμα)
2.

3.

4.

Τι ακριβώς ζητάει η άσκηση να κάνεις;;

Γιώργος · 08-09-11

Προστέθηκαν $\LaTeX$ tags, επειδή υπήρχε σοβαρός κίδυνος τα κλάσματα να ερμηνευθούν διαφορετικά.
debbie, εάν η άσκηση ΔΕΝ είναι έτσι όπως μορφοποίησα το post σου, να ενημερώσεις.

Η άσκηση τι ζητάει να κάνεις; Να "ανοίξεις" τους κλάδους;

debbie · 08-09-11

Παρακολουθώ τα μαθηματικά κατεύθυνσης και έχω κάτι ασκήσεις πάνω στις απόλυτες τιμές αλλά δεν μπορώ να λύσω αυτό το είδος!
βοηθήστε λιγάκι... :wacko:

1.|x|-1/|x|-2 (η κάθετος (/) δείχνει το κλάσμα)
2.x/1-|x|
3.x/|x|+1
4. |x+1|/|x-1|+2

Guest 010239 · 08-09-11

Αρχική Δημοσίευση από debbie:
Παρακολουθώ τα μαθηματικά κατεύθυνσης και έχω κάτι ασκήσεις πάνω στις απόλυτες τιμές αλλά δεν μπορώ να λύσω αυτό το είδος!
βοηθήστε λιγάκι...
1.|x|-1/|x|-2 (η κάθετος (/) δείχνει το κλάσμα)
2.x/1-|x|
3.x/|x|+1
4. |x+1|/|x-1|+2

Eκφωνηση δεν εχει η ασκηση?τι ζηταει?

debbie · 08-09-11

Να βρω για ποιες τιμές του χ ορίζονται τα ακόλουθα κλάσματα..!

g1wrg0s · 08-09-11

Σε ενα κλασμα πρωτα πρεπει να κοιτας ο παρανομαστης να μην ειναι 0. Βλεποντας τα κλασματα σου βλεπω οτι μονο αυτο τον περορισμο πρεπει να ελεγξεις.

dora9 · 18-09-11

εχω κατι ασκησουλες και με μπερδευουν λιγο οποιος μπορει ας βοηθησει :
1) αν ισχυει ΚΡ-ΑΡ=ΡΒ+ΛΡ να δειξετε οτι τα ΑΒ και ΛΚ ειναι αντιθετα
2) αν ισχυουν ΓΕ=ΒΡ και ΜΡ=ΒΚ να δειξετε οτι Ρ μεσο του ΕΚ
3)να δειξετε οτι ΑΔ+ΒΕ+ΓΖ=ΑΕ+ΒΖ+ΓΔ

Boom · 18-09-11

Δεν τα θυμάμαι καλά, νομίζω:
1.
ΚΡ-ΑΡ=ΡΒ+ΛΡ
-ΑΡ-ΡΒ=ΛΡ-ΚΡ
ΑΡ+ΡΒ=-ΛΡ+ΚΡ
ΑΒ=- (ΛΡ-ΚΡ)
ΑΒ=-ΛΚ

τα άλλα δοκίμασε να σπάσεις με κοινή αρχή.

Βοήθεια/Απορίες στα Μαθηματικά Προσανατολισμού - Ασκήσεις

Διάσημο μέλος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Διάσημο μέλος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Διάσημο μέλος

Πολύ δραστήριο μέλος

Διάσημο μέλος

Επιφανές μέλος

Διάσημο μέλος

Συνημμένα

Νεοφερμένο μέλος

Νεοφερμένο μέλος

Τιμώμενο Μέλος

Νεοφερμένο μέλος

Guest 010239

Επισκέπτης

Νεοφερμένο μέλος

Επιφανές μέλος

Νεοφερμένο μέλος

Επιφανές μέλος