Dias
Επιφανές μέλος


Αν α₁ , α₂ , … , αn θετικοί ≠ 1 , ν.δ.ο:
(1+α₁)∙(1+α₂)∙∙∙(1+αn) > 2ⁿ∙√α̅₁̅∙̅α̅₂̅∙̅∙̅∙̅α̅n̅
(Έχω κολλήσει πώς από το n πάει στο n+1)

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
13diagoras
Δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Αν α₁ , α₂ , … , αn θετικοί ≠ 1 , ν.δ.ο:Ειναι νιοστη ριζα , ν επι ριζα ή 2 στην ν? Αν ειναι η α' περιπτωση σαν πολυ ευκολη μου φαινεται..οποτε δεν νομιζω
(1+α₁)∙(1+α₂)∙∙∙(1+αn) > 2ⁿ∙√α̅₁̅∙̅α̅₂̅∙̅∙̅∙̅α̅n̅
Νομίζω ότι τώρα φαίνεται καλύτερα. (Τελικά την έλυσα, δεν ηταν και δύσκολη).


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
13diagoras
Δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Πρέπει να δείξουμε ότι: 1+αn+1 > 2∙√α̅n+1̅Ναι , ευκολη ειναι...τελικα αφου δειξουμε οτι ισχυει για ν=1,στο τελικο σταδιο αποδειξης προκυπτει το αν+1 +1>αν+1 ^ ½ που ισχυει

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
13diagoras
Δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vavlas
Εκκολαπτόμενο μέλος


2. Να βρείτε την εφαπτομένη της παραβολής C:y^2=4x ,η οποία τέμνει τους άξονες στα σημεία Α, Β και ειναι (ΑΒ)= ρίζα 2
Ευχαριστώωωωω!
Παραθέτω μια άσκηση στον κύκλο.
Να βρείτε την εξίσωση του C όταν εφάπτεται στον άξονα y'y στο σημείο A(0,3) και το κέντρο του ανήκει στην ευθεία ε:y=2x.
ΛΥΣΗ
(X-Xο)²-(Y-Y)²=ρ²
Ισχύει ΙxοΙ=ρ
Άρα (X-Xο)²-(Y-Yο)=Xο²
Α-->C
(0-Xο)²-(3-Υο)=Χο²
Επίσης Yo=2Χo
Οπότε (0-Xο)²-(3-2Χo)=Χο²
Χο²-Χο²-9+12Xo-4Xo²=0
-4Xo²+12Xo-9=0
Δ=0
Xo=-2α/β(=)Χο=12/8=3/2
Άρα C:(Χ-3/2)²-(Υ-3)²=9/4
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
niki6
Νεοφερμένο μέλος


y^2=4x 'αρα χ=y^2/4 <sxesh 1> έστω Μ ( χ1, y1) το σημειο επαφησ
η εφαπτομενη τησ παραβολησ εχει τυπο: yy1 = 2( x+ x1) αντικαθιστω το χ1 απο τη σχεση 1 και κανω και τισ πραξεισ και καταληγει:
y yi= 2x + y1^2/ 2 -> y1^2 - 2y y1 +4x = 0 < σχεση 2>
για χ=ο, αντικαθιστω στη παραπανω σχεση : y= y1/2 ara A= ( 0, y1/2 )
για y=o , x= -y1^2/4 ara B= (-y1^2/4 , 0)
(AB)= riza 2 -> riza ( (y1^2/4 )^2 + ( y1/2)^2 ) = riza 2 -> κανω τισ πραξεισ προκυπτει πολυωνυμο εξαιρω την αρνητικη ριζα επειδη ο αγνωστοσ ειναι τετραγωνο και τελικα έχω:
y1 = + ή - 2 αντικαθιστω στη σχεση 2 και.......
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vavlas
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Rempeskes
Επιφανές μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vavlas
Εκκολαπτόμενο μέλος



https://img441.imageshack.us/i/dsc00328jh.jpg/
https://img100.imageshack.us/i/dsc00329p.jpg/

Στην τελευταία έχω ένα λαθάκι καθώς βιαζόμουν.
Είναι Χ+Υ+1=0
Και Χ-Υ+1=0
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
guess
Δραστήριο μέλος


Μια άσκηση με οικογένεια ευθειών όποιος μπορει ας βάλει...
Με θέματα κατανοητά που μπορεί να πέσουν στις εξετάσεις..
Ευχαριστώ εκ των προτέρων =)
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Θα βρείς κάποιες στο θέμα αυτό πιο πριν. Να μια κλασική:Άσκηση με οικογένεια ευθειών
........

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
guess
Δραστήριο μέλος


που είναι ?
δεν βγαίνει ...μήπως πηγε βόλτα?

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
prinCess.
Επιφανές μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
savvass1
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Να βρειτε την εφαπτομενη της παραβολης C: y²=2x που απεχει απο την εστια της αποστασης 3√2̅/4
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
tasosple
Εκκολαπτόμενο μέλος


ο εγγεγραμμένος κύκλος ενός τριγώνου ΑΒΓ με Α(0,-5) είναι χ²+ψ²=5. Το σημείο επαφής της πλευράς ΒΓ με τον κύκλο είναι Δ(1,2) Να βρείτε : ι) τις εξισώσεις των πλευρών ΒΓ,ΑΒ,ΑΓ και ιι) τα σημεία που τέμνουν οι πλευρές ΑΒ και ΑΓ τον άξονα χχ'
και κατι αλλο να αποδειχθεί ότι το διάνυσμα ι²=1
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Δεν είναι δύσκολη: Η εξίσωση της ΒΓ βγαίνει αμέσως με τον τύπο και των άλλων είναι εφαπτόμενες από σημείο έξω από τον κύκλο σαν την 1η εφαρμογή του βιβλίου. Για τα σημεία τομής βάζεις y=0.ο εγγεγραμμένος κύκλος ενός τριγώνου ΑΒΓ με Α(0,-5) είναι χ²+ψ²=5. Το σημείο επαφής της πλευράς ΒΓ με τον κύκλο είναι Δ(1,2) Να βρείτε : ι) τις εξισώσεις των πλευρών ΒΓ,ΑΒ,ΑΓ και ιι) τα σημεία που τέμνουν οι πλευρές ΑΒ και ΑΓ τον άξονα χχ'
What is this?να αποδειχθεί ότι το διάνυσμα ι²=1

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vavlas
Εκκολαπτόμενο μέλος


Συγνώμη για το πολύ πρόχειρο σχήμα αλλά το έχω κάνει με την ζωγραφική.
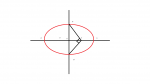
Έχω αυτή την έλλειψη(ο θεός να την κάνει)και θέλω να βρω την εκκεντρότητα ξέροντας μόνο ότι το ΒΕ είναι κάθετο στο ΕΒ'.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
- Status
- Το θέμα δεν είναι ανοιχτό για νέες απαντήσεις.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 16 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



