michos93
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
toi_toi
Πολύ δραστήριο μέλος


(δεν ξερω αν κανω καποιο λαθος)
2) εδω βγαινει οτι ο Α^2 ειναι διαγωνιος πινακας με τα στοιχεια στην διαγωνιο να ειναι το k^2 οποτε για να ειναι ισος με τον Α πρεπει k^2=k <=> k^2 - k = 0 <=> k(k-1)= 0 <=> k=0 ή k=1
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
michos93
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eua1993
Νεοφερμένο μέλος


α)(ΑχΒ)^4=Α^4χΒ^4
β)(Α-Β)^2=Α^2-2ΑΒ+Β^2
Υποδειξη:Να χρησιμοποιησουμε οσο γινεται πιο τυχαιους πινακες,δικους μας!
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
toi_toi
Πολύ δραστήριο μέλος


Να αποδειχθει οτι αν Α και Β ειναι τετραγωνικοι πινακες (εστω διαστασης 3χ3) ,τοτε ΔΕΝ ισχυουν (εν γενει) οι παρακατω σχεσεις:
α)(ΑχΒ)^4=Α^4χΒ^4
β)(Α-Β)^2=Α^2-2ΑΒ+Β^2
Υποδειξη:Να χρησιμοποιησουμε οσο γινεται πιο τυχαιους πινακες,δικους μας!
βιβλιο υποθετω εχεις! σωστα? προφανως θα λεει αναλυτικα πως γινεται ο πολ/σμος πινακων...πιασε δες την θεωρια και μετα βαλε τυχαια νουμερα στους πινακες κ κανε πραξεις!

βρηκα αυτο στο youtube... https://www.youtube.com/watch?v=s5-dXVacbEU
ισως σε βοηθησει!
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Evi235
Νεοφερμένο μέλος


1)περιγραψτε τις γραμμες του DA και τις στηλες του AD αν D=[2 0]
[0 5] .
2)υποθεστε οτι ο Α προκυπτει απο τον ταυτοτικο 4*4 πινακα με αντικατασταση της γραμμης 2 απο το διανυσμα u
Α=[1 u1 0 0]
[0 u2 0 0]
[0 u3 1 0]
[0 u4 0 1]
a) παραγοντοποιηστε τον σε γινομενο LU υποθετοντας οτι u2 != 0
β) βρειτε τον Α αντιστροφο που εχει την ιδια μορφη με τον Α
ευχαριστω εκ των προτερων. . .
????
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Evi235
Νεοφερμένο μέλος


[1 0 2 3]
[0 0 0 3]
[0 -1 2 0]
οποιος μπορει ας με βοηθησει το συντομοτερο δυνατο..ευχαριστω

επειγον...
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Evi235
Νεοφερμένο μέλος


να σε ρωτησω και κατι αλλο?
Δωστε τον πινακα προβολης πανω στον χωρο γραμμων ενος πινακα Α!
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


 . Θεωρία θα είναι, ψάξτο.
. Θεωρία θα είναι, ψάξτο.Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Evi235
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Είδα από ένα βιβλίο τον τρόπο για τον χώρο στηλών και προσπάθησα να κάνω το ίδιο για τον χώρο γραμμών χωρίς να θυμάμαι καθόλου την θεωρία. Πιστεύω όμως ότι είναι σωστό διότι αν διαλέξω ένα διάνυσμα b που ανήκει στον χώρο γραμμών (
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Evi235
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Να μία μέθοδος η οποία επεκτείνεται για αθροίσματα της μορφήςΠοιός είναι ο κλειστός τύπος του αθροίσμτος: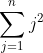
Έστω
Εναλλακτικά το άθροισμα αυτό υπολογίζεται και ως εξής
Εξισώνοντας τις δύο εκφράσεις και λύνοντας ως προς S παίρνουμε
Παρατήρησε ότι θεωρούμε γνωστό το άθροισμα
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
songoku
Νεοφερμένο μέλος


1)να βρεθούν οι πέντε πρώτοι όροι της σειράς maclaurin , f(x)= 2x(x^2+1)/(1-x^2)^2, |x|<1
2)10^2-9^2+8^2-7^2+....+2^2-1^2
3)2^x+4=1/16
4)lnx+ln(x+2)=0
5)2^x+1=3/8
6)|x-1|<4
7)|x-1|=4
8 ) |x-1|>4
9)α/1+|α|=β / 1+|β| =|α|= |β|
10)|χ+2|+|χ-4|=0
11) να βρεθεί η παράγωγος f(y)=12-3y^2-8ρίζα (12-3y^2)+16+y^2-4y+4
12)lim 2^x-2^-x/2^x+2^-x όταν το χ τείνει στο +00
13)lim εφχ+ημχ/χ^3 όταν το χ τείνει στο 0
14)lim(2x+4/2x+1)^3x+1 όταν το χ τείνει στο +00
Σας παρακαλώ πολύ αν μπορεί κάποιος να μου τις λύσει άμεσα, ευχαριστώ πολύ για τον χρόνο σας!
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paladin_k20
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


https://en.wikipedia.org/wiki/Taylor_series#Taylor_series_in_several_variablesΝα βρεθει μια πολυωνυμικη καμπυλη 2ου βαθμου η οποια θα προσεγγιζει τηνστη γειτονια του σημειου (1,0).
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paladin_k20
Εκκολαπτόμενο μέλος


Ξερω οτι χρειαζεται Τaylor...το θεμα ειναι οτι πρεπει να βρω ΚΑΜΠΥΛΗ y=f(x) απο αυτην που μου δινει.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Πολύ ωραία, θα πάρεις 2ης τάξης (αφού θέλεις 2ου βαθμού πολυώνυμο) προσέγγιση Taylor για τη συνάρτηση δύο μεταβλητώνΞερω οτι χρειαζεται Τaylor...το θεμα ειναι οτι πρεπει να βρω ΚΑΜΠΥΛΗ y=f(x) απο αυτην που μου δινει.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 24 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



