Demlogic
Πολύ δραστήριο μέλος


i) Πράξεις
ii) Ισχύει ότι.
Απόδειξη
^2+(y-z)^2+(x-z)^2)
που ισχύει. Επομένως
λόγω του ερωτήματος i)
πολυ ωραια άσκηση. απορώ πως δε πρόσεξα την ταυτότητα
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Alejandro che 7
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
IasonasM
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


Εχουμε z=-1/2 +/- ριζα3/2 iΑν z^2+z+1=0 να αποδειξετε οτι z^65+(1/z^65)=-1
z1^2=-1/2 -ριζα3/2 i και z2^2 = -1/2+ριζα3/2 i (z1 ο συζυγης του z2)
z1^3=1 και z2^3=1
Το μετρο του z ειναι 1 αρα z1z2=1 και z1=1/z2
z^65 + 1/z^65 =z1^65 + z2^65=(z1^3)^21x z1^2 +(z2^3)^21x z2^2=z1^2 + z2^2=-1/2-ριζα3/2i -1/2+ριζα3/2i=-1
Σορρυ αν σας βγηκαν τα ματια θα μαθω καποια στιγμη latex.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mercury
Επιφανές μέλος


Αν z^2+z+1=0 να αποδειξετε οτι z^65+(1/z^65)=-1
Θα δοκιμάσω μία διαφορετική προσέγγιση,πείτε μου άν είναι σωστή ή λάθος:
Απο την δευτεροβάθμια παίρνουμε,με βάση τους τύπους του Vietta:
Επίσης:
Οπότε έχουμε:
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Αν z^2+z+1=0 να αποδειξετε οτι z^65+(1/z^65)=-1
Ένας άλλος τρόπος είναι να λύσουμε την δευτεροβάθμιας εξίσωση με λύσεις z1, z2=συζυγήςz1 (εφοσον Δ=-3<0). Στη συνέχεια βρίσκουμε με θεώρημα De Moivre τα (z1^65) και (z1^(-65)) και τα προσθέτουμε. Εφόσον ισχύει η αποδεικτέα σχέση για τον z1 θα ισχύει και για τον z2 εφόσον είναι συζυγής του z1.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος



οπου z1 ο συζυγης του z
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Να βρειτε το μετρο του μιγαδικου z για τον οποιο ισχυει

οπου z1 ο συζυγης του z
Μπορείς να δυσκολέψεις λίγο παραπάνω την άσκηση ζητώντας να βρεθούν οι μιγαδικοί αριθμοί z για τους οποίους ισχύει η δοσμένη σχέση. (Πρέπει να είναι οι z1=-1, και z2=3-4i)
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


Αυτο λυνεται νομιζω με x+yi ετσι;Μπορείς να δυσκολέψεις λίγο παραπάνω την άσκηση ζητώντας να βρεθούν οι μιγαδικοί αριθμοί z για τους οποίους ισχύει η δοσμένη σχέση. (Πρέπει να είναι οι z1=-1, και z2=3-4i)
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Αυτο λυνεται νομιζω με x+yi ετσι;
Όχι δε χρειάζεται. Απλά εκμεταλλευόμαστε τις ταυτότητες |z_|=|-z|=|z| (z_ ο συζυγής του z). Συνεπώς η σχέση γράφεται ισοδύναμα:
z=(|z|-2)+(1-|z|)i (1)
Άρα έχουμε
|z|^2=[(|z|-2)^2]+[(1-|z|)^2] => |z|^2=2(|z|^2)-6|z|+5 => (|z|^2)-6|z|+5=0 => (|z|^2)-6|z|+9-4=0 =>
=> [(|z|-3)^2]-4=0 => (|z|-3-2)(|z|-3+2)=0 => (|z|-5)(|z|-1)=0 => |z|=5 ή |z|=1
Αν |z|=1 τότε από την (1) προκύπτει z=-1 (πράγματι |z|=|-1|=1)
Αν |z|=5 τότε από την (1) προκύπτει z=3-4i (πράγματι |z|=SQRT((3^2)+((-4)^2))=SQRT(25)=5)
Άρα z1=-1, |z1|=1 και z2=3-4i, |z2|=5
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
κατερω
Εκκολαπτόμενο μέλος


Αν z^2+z+1=0 να αποδειξετε οτι z^65+(1/z^65)=-1
Κάτι δε μου αρέσει στη λύση μου..
Αρχικά είναι στην υπόθεση ότι z=/0 αφού είναι σε παρονομαστή, έτσι;
z^2 + z + 1 = 0
άρα (z-1)(z^2+z+1) = 0
άρα z^3 - 1 = 0
και έτσι z^3 = 1
τώρα κάνω τη διαίρεση 65 = 3*21 +2
άρα με δεδομένο το ζητούμενο
z^65 + 1/ z^65 = -1
γράφεται z^ (3*21 + 2) + 1/ z (^3*21 + 2) = -1
και αφού z^3 κάνει 1 μένει ότι z^2 + 1/ z^2 + 1 = 0
πολλ/ζω με z^ 2
και έχω z^4 + z^2 + 1 = 0
αντικαθιστώ το z^2 + 1 με -z (από αρχική συνθήκη αφού z^2 + z + 1 = 0)
και έχω z^4 - z = 0
κοινό παράγοντα
z (z^3 - 1) = 0
z =/ 0 από υπόθεση αφού σε παρονομαστή
z^3 = 1 που ισχύει!
Κάνω κάτι λάθος??
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
unπαικτable
Πολύ δραστήριο μέλος


(βασανο μεγαλο ο συντακτης LATEX, χειρογραφο και παλι χειρογραφο για τα μαθηματικοφυσικα)
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mamaguena
Εκκολαπτόμενο μέλος


({z}^{2}+z+1)=0\Leftrightarrow {z}^{3}-1=0\Leftrightarrow {z}^{3}=1 )
(βασανο μεγαλο ο συντακτης LATEX, χειρογραφο και παλι χειρογραφο για τα μαθηματικοφυσικα)
Αρχικά, πρέπει να αποδείξεις ότι
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
unπαικτable
Πολύ δραστήριο μέλος


Αρχικά, πρέπει να αποδείξεις ότιμε άτοπο, εφόσον πολλαπλασιάζεις με το
 )
Πολλαπλασιασμο εκανα, δεν χρειαζεται να παρω περιορισμο.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mamaguena
Εκκολαπτόμενο μέλος


Πολλαπλασιασμο εκανα, δεν χρειαζεται να παρω περιορισμο.
Εφόσον έβαλες
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


z^65+(1/z^65)=-1=> (z^65)^2 +z^65 +1=0 ==(1)==> ισχυει.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ξαροπ
Πολύ δραστήριο μέλος


Άμα ήταν μέσα και το θεώρημα de Moivre και η τριγωνομετρική / πολική μορφή μιγαδικών θα 'χαμε ωραία πράματα να πούμε αλλά δεν είναι...οπότε μόκο εκτός αν ενδιαφέρεται κανείς.

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Νδο. η εξίσωσηδεν έχει λύση στους πραγματικούς.
Άμα ήταν μέσα και το θεώρημα de Moivre και η τριγωνομετρική / πολική μορφή μιγαδικών θα 'χαμε ωραία πράματα να πούμε αλλά δεν είναι...οπότε μόκο εκτός αν ενδιαφέρεται κανείς.
Έστω
Για x=0 στην αρχική σχέση προκύπτει:
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


i) Νδο
ii) Να βρείτε τις τιμές του
iii)Νδο
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
κατερω
Εκκολαπτόμενο μέλος


Δίνεται ο μιγαδικός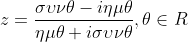
i) Νδο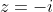
ii) Να βρείτε τις τιμές του, για τις οποίες ισχύει
iii)Νδο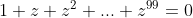
Τα i) και iii) νομιζω βγηκαν ευκολα το ii δεν το προσπαθησα αρκετα θα το ξαναδω..
(δεν το καταφερα το LaTeX
 )
)i) z = συνθ - ημθi / -ημθi^2 + συνθ i
z = συνθ - ημθ i / -i (ημθi - συνθ)
z = - (ημθ i - συνθ) / -i (ημθi - συνθ)
z = 1/ i
z = -i
iii) γεωμετρικη προοδος με α1 = z και λ = z
αρκει νδο z + z^2 + .... + z^99 = -1
S(99) = α1 [ (λ^ν - 1) / λ-1 ]
S = z (z ^99 - 1) /z-1
S = -i [ (-i)^99 -1 ] / -i-1
S = -i (i^99 + 1) /i + 1
S = i ^2 -i / i + 1
S = -1 -i / 1 +i
S = -1
αρα το δειξαμε..
για το ii κατι μου διαφευγει προς το παροοον
Νομίζω ξελαμπήκαρα

ii) (1 -z )^n = (1 + z) ^n
(1 + i)^n = (1 -i)^n
(1 + i)^n = (-i^2 -i)^n
(1+i)^n = (-i)^n (1 + i)^n
(-i)^n = 1
n = 4ρ, ρ ε Z?
το χασα??
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

