Ασκήσεις μαθηματικών για ΑΕΙ

termitis · 22 Απριλίου 2010 στις 15:29

[FONT=&quot]Να αποδείξετε ότι το σύνολο [/FONT][FONT=&quot]V[/FONT][FONT=&quot] [/FONT][FONT=&quot]των στοιχείων (x1,x2,x3,x4) με xi e R[/FONT][FONT=&quot] και x1+x2=x3-x4=0 είναι διανυσματικός χώρος και να βρείτε μία βάση του.
Το προβλημα μου είναι το 1ο ερωτημα!δεν μασ εχει πει ο καθηγητης πως δειχνεις οτι ενα σύνολο είναι διανυσματικός χώρος!Παρακαλώ αν είναι καποιος γνώστης να με βοηθήσει!ευχαριστω προκαταβολικα!

[/FONT]

exc · 23 Απριλίου 2010 στις 22:53

Αρχική Δημοσίευση από termitis:
[FONT=&quot]Να αποδείξετε ότι το σύνολο [/FONT][FONT=&quot]V[/FONT][FONT=&quot]των στοιχείων (x1,x2,x3,x4) με xi e R[/FONT][FONT=&quot] και x1+x2=x3-x4=0 είναι διανυσματικός χώρος και να βρείτε μία βάση του.
Το προβλημα μου είναι το 1ο ερωτημα!δεν μασ εχει πει ο καθηγητης πως δειχνεις οτι ενα σύνολο είναι διανυσματικός χώρος!Παρακαλώ αν είναι καποιος γνώστης να με βοηθήσει!ευχαριστω προκαταβολικα!
[/FONT]

Ένας ανυσματικός χώρος έχει 8 ιδιότητες. (Φαντάζομαι αυτό θα το έχει αναφέρει ο καθηγητής σου).
Πρέπει να δείξεις ότι ο ανυσματικός χώρος V έχει αυτές τις ιδιότητες.

https://el.wikipedia.org/wiki/Διανυσματικός_χώρος

termitis · 24 Απριλίου 2010 στις 00:52

Ευχαριστώ πολυ για το ενδιαφέρον σου!είσαι ο μόνος!το εκτιμώ...

riemann80 · 28 Απριλίου 2010 στις 21:18

θα πρεπει να δειξεις τα εξης

1) το αθροισμα δυο στοιχειων του συνολου ειναι παλι στοιχειο του συνολου

2) καθε πολλαπλασιο του τυχοντος στοιχειου του συνολου ειναι παλι στοιχειο του συνολου

τοτε θα χεις δειξει οτι το συνολο σου ειναι υποχωρος του R^4 αρα διανυσματικος χωρος

για το 1) ας πουμε παρε δυο στοιχεια (α,β,γ,δ) και (χ,ψ,ζ,ω) μεσα απο το συνολο δηλαδη ισχυουν α+β=γ-δ=0 και χ+ψ=ζ-ω=0 προσθετωντας τα δυο στοιχεια εχουμε (α,β,γ,δ)+(χ,ψ,ζ,ω)=(α+χ,β+ψ,γ+ζ,δ+ω) και λογω των αρχικων σχεσεων εχουμε (α+χ)+(β+ψ)=(γ+ζ)-(δ+ω)=0 που δειχνει οτι το (α+χ,β+ψ,γ+ζ,δ+ω) ειναι ξανα στοιχειο του συνολου.αναλογως πραττεις στο (2).

οσο για τη βαση παρε το τυχον (α,β,γ,δ) και εχει α=-β = γ=δ αρα (α,β,γ,δ)=(α,-α,α,α)=α(1,-1,1,1) αρα ο υποχωρος εχει διασταση 1 και μια βαση του ειναι η {(1,-1,1,1)}.

tweetyslvstr · 2015-09-10T17:47:52+0300

Καλησπέρα παιδιά !!! Ερωτηση
Γνωρίζει κανείς τι γίνεται με τις σειρές ολοκλήρωσης?? Κανένα εγγραφο που να δείχνει τι γίνεται?? Πως καταλαβαίνω ότι πρέπει να αλλάξω την σειρά ολοκλήρωσης ??? Υπάρχει κανένα θεώρημα???
Βοηθεια!!!!

Εάν ξερει κανεις, ας απαντησει!!

Bemanos · 2015-09-16T14:26:38+0300

Εχω σκαλωσει στο παρακατω θεμα . Σπαει το κλασμα για να βρει τους συντελεστες ,ετσι ,ωστε να γινει η ολοκληρωση μετα ,αλλα δεν καταλαβαινω γιατι το σπαει σε 3 μερη Εγω το εχω σπασει σε 2 δηλαδη A/(Αο-2χ)^2 + Β(Βο-χ)
Να δεχτω να το σπασει σε 3 της μορφης Α/(Αο-2χ)+Β(Αο-2χ)+Γ(Βο-χ) ,αλλα αυτος κραταει και το τετραγωνο .Κανω εγω κατι λαθος ,ή αυτος είναι λάθος

Vold · 2015-09-16T14:38:18+0300

Έτσι γίνεται όταν σπας ένα κλάσμα σε μερικά κλάσματα.
Αν αντί να ήταν υψωμένο στο τετράγωνο ήταν εις τον κύβο(δλδ το Α/(Αο - 2x)^ 2 του αρχικού κλάσματος σε Α/(Αο - 2x) ^ 3), τότε θα είχε ακριβώς έναν επιπλέον παράγοντα όπως τον πρώτο( Α/(Αο - 2x) ), αλλά υψωμένο εις τον κύβο

Μπορείς να ρίξεις μια ματιά ΕΔΩ, αν θες.

Bemanos · 2015-09-16T14:54:54+0300

αα ,καταλαβα ,θενξ !

Vold · 1 Οκτωβρίου 2015 στις 17:55

Ειλικρινά, ή εγώ κάνω @!@$! ή υπάρχει κάποιο λάθος...

Είπα:

Και μετά ότι P[M] = 4/5 * P[A] αλλά βγαίνει αρνητική διακρίνουσα
Αυτό το 4/5 ερμηνεύεται κάπως αλλιώς ; Δεν θέλω λύση, απλά ένα "σπρώξιμο" ώστε να ξεμπλοκάρω.

PeterTheGreat · 1 Οκτωβρίου 2015 στις 18:11

P(M) = P(A) + 4/5 δεν εννοεί?

Vold · 1 Οκτωβρίου 2015 στις 18:26

ΟΚ, εντάξει, βγαίνει έτσι.
Τι μλκας που είμαι... και το δοκίμασα να φανταστείς χθες και δεν έβγαινε :whatever:

Thanks

unπαικτable · 2016-02-15T20:16:08+0200

Καποιος μερακλης αμα μπορει να βοηθησει με το παρακατω.

Δινεται η ακολουθια ${\alpha }_{n}=\frac{{1}^{k}+{2}^{k}+...+{n}^{k}}{{n}^{k+1}}$
Νδο
$\lim_{n\rightarrow \infty} {\alpha }_{n}=\frac{1}{k+1}$

nPb · 2016-02-15T20:57:02+0200

Θα την κοιτάξω.

unπαικτable · 2016-02-15T21:06:41+0200

Η λυση ομως μου δινει το οριο και για k=499 ας πουμε. Εκει πως να κανω επαγωγη;

nPb · 2016-02-15T22:22:19+0200

Αρχική Δημοσίευση από unπαικτable:
Καποιος μερακλης αμα μπορει να βοηθησει με το παρακατω.

Δινεται η ακολουθια ${\alpha }_{n}=\frac{{1}^{k}+{2}^{k}+...+{n}^{k}}{{n}^{k+1}}$
Νδο
$\lim_{n\rightarrow \infty} {\alpha }_{n}=\frac{1}{k+1}$

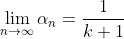
Κάνουμε επαγωγή καθώς ισχύει για κάθε k φυσικό.

Ξεκινάμε με k=0: Ο αριθμητής της ακολουθίας είναι 1+1+1+...+1=1n=n (n φορές το 1). Ο παρονομαστής της ακολουθίας είναι n οπότε η ακολουθία συγκλίνει σταθερά στο 1. Ανεβαίνουμε στο k=1: Ο αριθμητής της ακολουθίας είναι το γνωστό άθροισμα 1+2+3+...+n το οποίο κάνει n(n+1)/2. O παρονομαστής είναι n με εκθέτη 2. Κάνουμε το σύνθετο κλάσμα απλό και έχουμε:

$\alpha _{n}=\frac{n(n+1)}{2n^{2}}=\frac{1}{2}+\frac{1}{2n}$

Καθώς το n τρέχει στο άπειρο (+ ή -) η ακολουθία συγκλίνει σταθερά στο 1/2 (από ιδιότητες ορίου ακολουθιών και ότι 1/2n καθώς το n τρέχει στο άπειρο, μηδενίζεται).

Συνεχίζουμες επαγωγικά για κάθε φυσικό αριθμό μ. Θα πρέπει να δείξουμε ότι ισχύει και για μ+1.
(βλέπεις στο post #16)

nPb · 2016-02-15T23:23:35+0200

Έστω ότι ισχύει για κάποιο μ φυσικό. Τότε:

$\alpha _{n}=\frac{1^{\mu }+2^{\mu }+...+n^{\mu }}{n^{\mu +1}} \rightarrow \frac{1}{\mu +1}$

καθώς το n τείνει στο άπειρο. Θα δείξουμε ότι ισχύει για τον φυσικό αριθμό μ+1. Πράγματι, έχουμε την ακολουθία

$\alpha _{n}=\frac{1^{\mu+1 }+2^{\mu+1 }+...+n^{\mu+1 }}{n^{\mu +2}}$

και αν θέσουμε όπου ω το μ+1 τότε,

$\alpha _{n}=\frac{1^{\omega }+2^{\omega }+...+n^{\omega }}{n^{\omega +1}}$

το οποίο είναι γνωστό αποτέλεσμα, για κάθε φυσικό αριθμό καθώς το n φεύγει στο άπειρο. Άρα, έχουμε καθώς το n φεύγει στο άπειρο

$\alpha _{n}=\frac{1^{\omega }+2^{\omega }+...+n^{\omega }}{n^{\omega+1}} \rightarrow \frac{1}{\omega +1}$

δηλαδή, καθώς το ω είναι το μ+1 με αναδρομική αντικατάσταση η προηγούμενη οριακή διαδικασία γράφεται:

$\alpha _{n}=\frac{1^{\mu+1 }+2^{\mu+1 }+...+n^{\mu+1 }}{n^{\mu+2}} \rightarrow \frac{1}{\mu+2}$

που σημαίνει ότι ισχύει για κάθε φυσικό αριθμό k._

tsigaraki · 2016-02-21T12:11:09+0200

Θα ηθελα να επισημανω δημοσια το λαθεμενο της παραπανω αποδειξης .

Θα παρακαλουσα τους φοιτητες να μην παραπλανηθουν απο την παραπανω αποδειξη .

manolis_98 · 2016-10-21T16:43:24+0300

προσδιορίστε τα ακόλουθα αθροίσματα Minkowski: [0,1] + [2,3], Z+ (0,1), Z+ [0,1], Q+Q, Q+ (R−Q). Μπορείτε να χρησιμοποιήσετε το γεγονός ότι δύο σύνολα είναι ίσα αν και μόνο αν το ένα είναι υποσύνολο του άλλου και αντιστρόφως.
παίδες κάποια εξήγηση του τρόπου λύσης
(υπόδειξη: Εκτός από την ένωση και την τομή, μπορούμε να ορίσουμε και το άθροισμα δύο συνόλων. Συγκεκριμένα, ορίζουμε το άθροισμα Minkowski A+B δύο συνόλων A, B, ως το νέο σύνολο που αποτελείται από όλους τους αριθμούς z που μπορούν να γραφούν ως το άθροισμα ενός αριθμού a που ανήκει στο A και ενός αριθμού b που ανήκει στο B: A + B ={z ∈R : z = a + b, a ∈ A, b ∈ B}. )

unπαικτable · 2016-10-21T19:17:50+0300

Αρχική Δημοσίευση από manolis_98:
προσδιορίστε τα ακόλουθα αθροίσματα Minkowski: [0,1] + [2,3], Z+ (0,1), Z+ [0,1], Q+Q, Q+ (R−Q). Μπορείτε να χρησιμοποιήσετε το γεγονός ότι δύο σύνολα είναι ίσα αν και μόνο αν το ένα είναι υποσύνολο του άλλου και αντιστρόφως.
παίδες κάποια εξήγηση του τρόπου λύσης
(υπόδειξη: Εκτός από την ένωση και την τομή, μπορούμε να ορίσουμε και το άθροισμα δύο συνόλων. Συγκεκριμένα, ορίζουμε το άθροισμα Minkowski A+B δύο συνόλων A, B, ως το νέο σύνολο που αποτελείται από όλους τους αριθμούς z που μπορούν να γραφούν ως το άθροισμα ενός αριθμού a που ανήκει στο A και ενός αριθμού b που ανήκει στο B: A + B ={z ∈R : z = a + b, a ∈ A, b ∈ B}. )

Αν και δε ξερω σαν εννοια το αθροισμα Minkowski(μονο τον χωρο Minkowski ειχα υποψιν) απο αυτα που εγραψες νομιζω πως οι απαντησεις ειναι οι εξης:

(1): $\begin{cases} & a\in A \\ & b\in B \end{cases} \Rightarrow \begin{cases} & 0\leq a\leq 1 \\ & 2\leq b\leq 3 \end{cases} \Rightarrow 2\leq a+b\leq 4 \Rightarrow A+B=[2,4]$

(2), (3): $Z= \begin{Bmatrix}0, \pm1, \pm2 ,\pm3, ...\end{Bmatrix} , A=(0,1) .$ . Αρα εχεις ολους τους ακεραιους και ολα τα δεκαδικα ψηφια που μπορει να εχει ενας μη ακεραιος. Αρα το αθροισμα αυτων των δυο σου δινει το R(συνολο πραγματικων).

Δεν μπορω να βρω ουσιαστικη διαφορα μεταξυ ανοιχτου (0,1) και κλειστου [0,1] αφου στην πραγματικοτητα η αθροιση του 0 ή του 1 σε καποιο στοιχειο του Ζ παραγει στοιχειο το οποιο ηδη ανηκει στο Ζ.

(4) Το Q ειναι το σωμα των ρητων. Αν προσθεσεις δυο ρητους ο αριθμος ειναι επισης ρητος αφου προφανως μπορει να γραφει σε μορφη α/β οπου α/β ακεραιοι. Αρα το Q+Q= Q.

(5) Το (R-Q) συνολο ειναι το συνολο των αρρητων. Δεδομενου λοιπον οτι εχεις το αθροισμα κατα minkowski των συνολων των ρητων και των αρρηστων και ξεροντας οτι (ρητος)+(αρρητος)=(αρρητος) οι μονοι δυνατοι αριθμοι που μπορουν να προκυψουν ειναι οι αρρητοι. Αρα Q+(R-Q)=(R-Q)

manolis_98 · 2016-10-21T19:39:10+0300

Ευχαριστώ για τη βοήθεια!

Ασκήσεις μαθηματικών για ΑΕΙ

Νεοφερμένο μέλος

Διάσημο μέλος

Νεοφερμένο μέλος

Εκκολαπτόμενο μέλος

Δραστήριο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Επιφανές μέλος

Πολύ δραστήριο μέλος

Επιφανές μέλος

Επιφανές μέλος

Νεοφερμένο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος