Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.124 μηνύματα.

21-09-23

18:27
Μωρέ τα μαθηματικά είναι άπειρα πλέον σε γνώση αυτό είναι δεδομένοΣτα μαθηματικά έχει αρκετά
 .
.Θες να γίνεις λίγο πιο συγκεκριμένος ; Τι ακριβώς δηλαδή δεν κάνουν που χρειάζεται στον ηλεκτρομαγνητισμό ;η ένσταση η δικιά μου βρίσκεται κυρίως στο ότι δεν εμβαθύνουν τόσο επικαμπύλια για να κάνουν πιο προχωρημένο ηλεκτρομαγνητισμό.
41%
Εκκολαπτόμενο μέλος
Ο 41% αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών και Μαθητής Δημοτικού. Έχει γράψει 250 μηνύματα.

21-09-23

18:31
Από ύλη δεν νομίζω ότι δεν κάνουν κάτι σημαντικό, ισχύει για όλα τα ημμυ, αλλά να μωρέ αν πάρεις κάποιο από τα συγγράματα και προσπαθήσεις να λύσεις πιο εξεζητημένα θέματα με τα επικαμπύλια θα βρεις δυσκολίες.Θες να γίνεις λίγο πιο συγκεκριμένος ; Τι ακριβώς δηλαδή δεν κάνουν που χρειάζεται στον ηλεκτρομαγνητισμό ;
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.124 μηνύματα.

21-09-23

18:44
Γιατί ρε'συ ; Δεν υπάρχει περίπτωση να μην τα κάνουν στην ανάλυση ΙΙ . Αλλά ακόμα και εκεί να μην τα κάνουν τα κάνουν στα αντίστοιχα μαθήματα . Το οποίο είναι και το πιο σωστό κατ'εμέ . Εαν ο άλλος θέλει να ασχοληθεί με αρντουίνα και τέτοια , δεν έχει νόημα να τον σαπίζεις σε υποχρεωτικά μαθήματα προχωρημένων μαθ που πιθανότατα δεν θα χρειαστεί ποτέ του .Από ύλη δεν νομίζω ότι δεν κάνουν κάτι σημαντικό, ισχύει για όλα τα ημμυ, αλλά να μωρέ αν πάρεις κάποιο από τα συγγράματα και προσπαθήσεις να λύσεις πιο εξεζητημένα θέματα με τα επικαμπύλια θα βρεις δυσκολίες.
Για να είμαι ειλικρινής και εγώ που τα έχω κάνει , σε καθημερινό επίπεδο δεν πρόκειται προφανώς να κάτσω να λύνω επικαμπύλια ολοκληρώματα για να κάνω την δουλειά μου . Για την ακρίβεια κάποια στιγμή είχα παρακολουθήσει και ανάλυση Ι όπως την κάνουν στο μαθηματικό . Εαν και εμβαθύνεις πολύ , εμένα αυτό που μου έμεινε είναι οτι για τον μηχανικό τουλάχιστον δεν προσφέρεται κάτι που θα τον βοηθήσει ιδιαίτερα στην δουλειά του . Χωρίς να σημαίνει φυσικά οτι δεν χρειάζεται κάποιος να τα έχει θεμελιώσει σωστά αυτά τα πράγματα .
41%
Εκκολαπτόμενο μέλος
Ο 41% αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών και Μαθητής Δημοτικού. Έχει γράψει 250 μηνύματα.

21-09-23

18:56
ε ναι είναι και με το τι θέλει να ασχοληθεί ο καθέναςΕαν ο άλλος θέλει να ασχοληθεί με αρντουίνα και τέτοια
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.124 μηνύματα.

21-09-23

21:54
Πλέον η αλήθεια είναι πως οτι δεν έχει τεχνητή νοημοσύνη πάει κατά διαόλου .ε ναι είναι και με το τι θέλει να ασχοληθεί ο καθένας
Είμαστε way past απο τις εποχές που θα είχες όγκο φοιτητών να απασχολούνται με προβλήματα σε συγγράματα με την ανεργία να καλπάζει . Δυστυχώς ή ευτυχώς , δεν ξέρω , θα δείξει στο μέλλον .
ιωαννηs
Επιφανές μέλος
Ο ιωαννηs αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 15.422 μηνύματα.

22-09-23

13:15
Παμε πισω στην ομορφια της νευτωνιας φυσικης
Η ασκηση συτη εχει και προεκτασεις απο την καθημερινη μας ζωη.
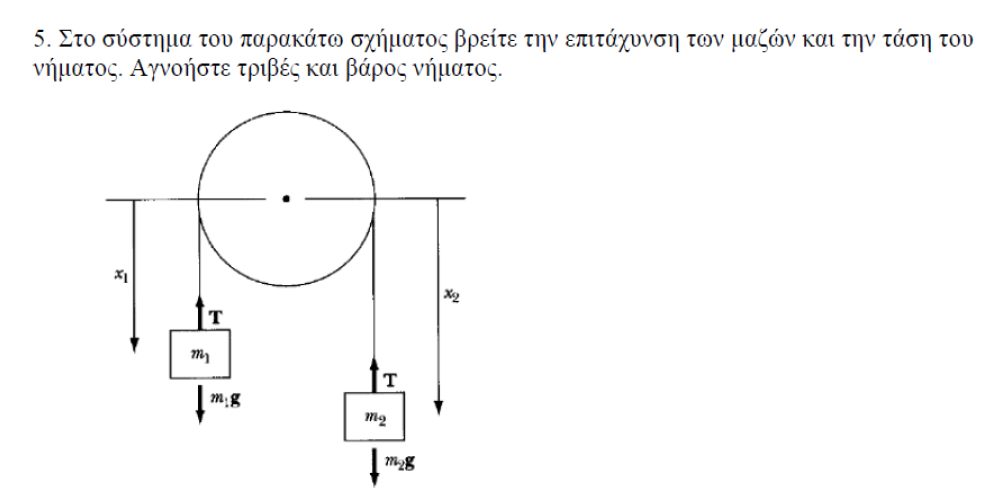

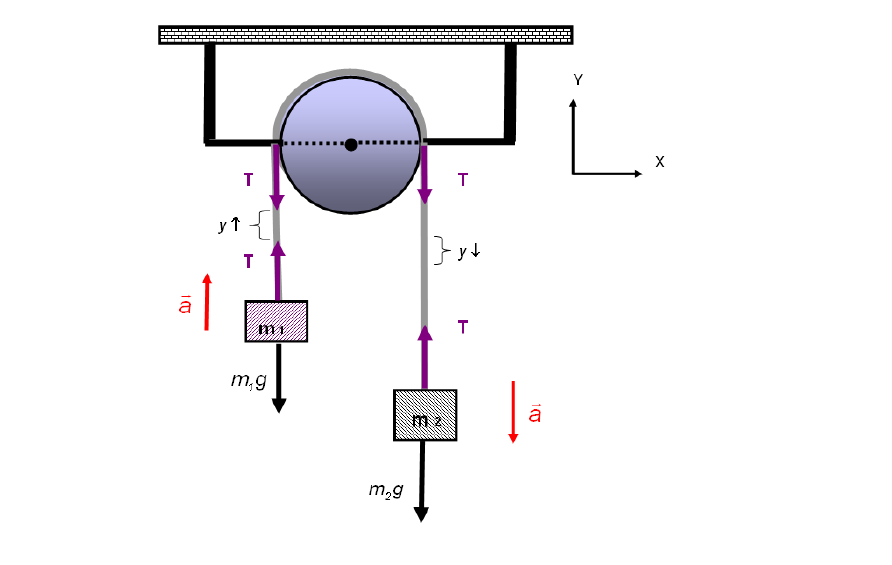

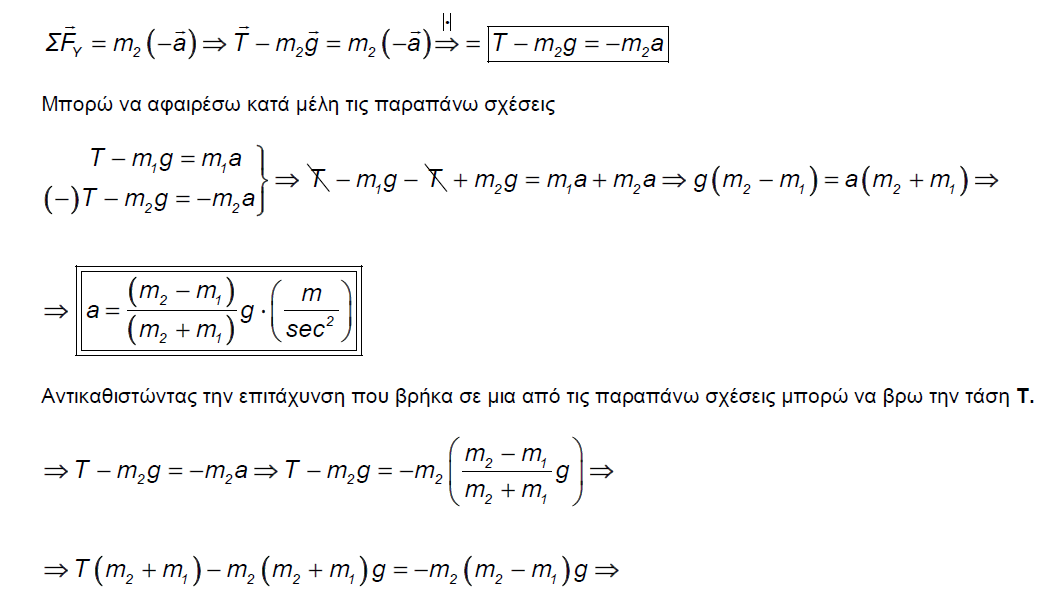

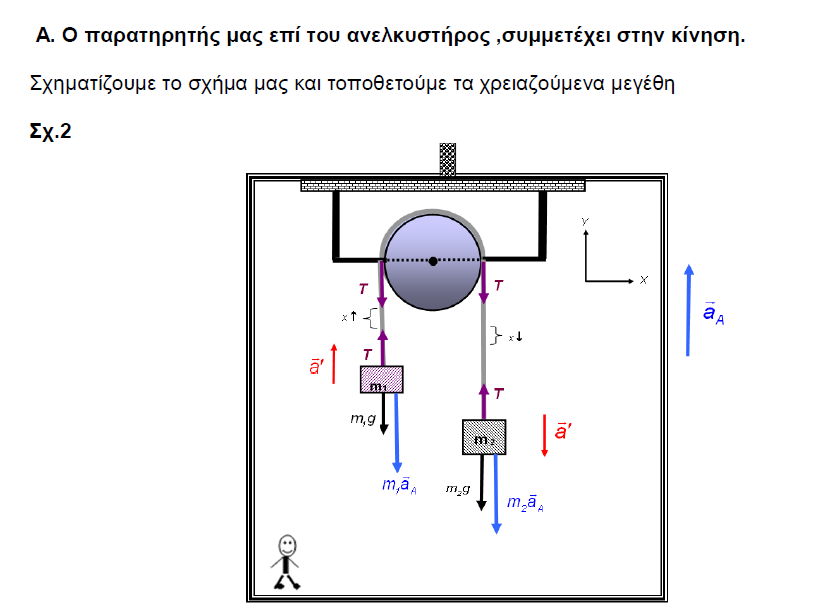









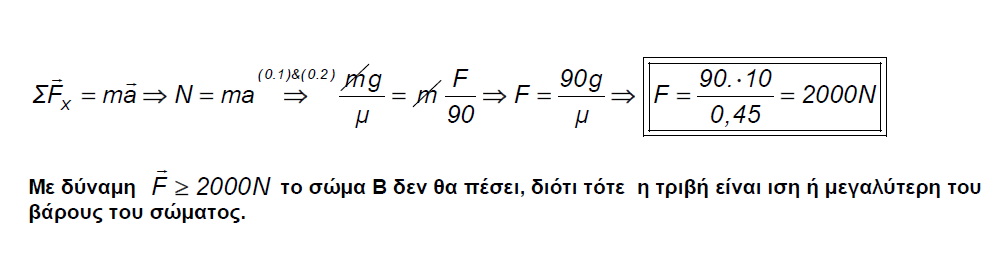
Η ασκηση συτη εχει και προεκτασεις απο την καθημερινη μας ζωη.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Συνημμένα
-
 1695377193666.png24 KB · Εμφανίσεις: 201
1695377193666.png24 KB · Εμφανίσεις: 201 -
 1695377222286.png23,1 KB · Εμφανίσεις: 229
1695377222286.png23,1 KB · Εμφανίσεις: 229 -
 1695377252843.png56,2 KB · Εμφανίσεις: 228
1695377252843.png56,2 KB · Εμφανίσεις: 228 -
 1695377297114.png62,2 KB · Εμφανίσεις: 213
1695377297114.png62,2 KB · Εμφανίσεις: 213 -
 1695377339529.png91,4 KB · Εμφανίσεις: 211
1695377339529.png91,4 KB · Εμφανίσεις: 211 -
 1695377367037.png39 KB · Εμφανίσεις: 232
1695377367037.png39 KB · Εμφανίσεις: 232 -
 1695377403319.png57,1 KB · Εμφανίσεις: 202
1695377403319.png57,1 KB · Εμφανίσεις: 202 -
 1695377430384.png66,8 KB · Εμφανίσεις: 221
1695377430384.png66,8 KB · Εμφανίσεις: 221 -
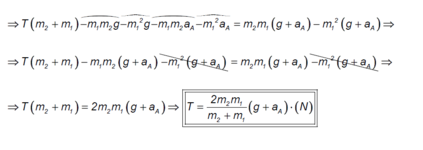 1695377457746.png33,4 KB · Εμφανίσεις: 152
1695377457746.png33,4 KB · Εμφανίσεις: 152 -
 1695377496337.png40,8 KB · Εμφανίσεις: 128
1695377496337.png40,8 KB · Εμφανίσεις: 128 -
 1695377530209.png27,6 KB · Εμφανίσεις: 219
1695377530209.png27,6 KB · Εμφανίσεις: 219 -
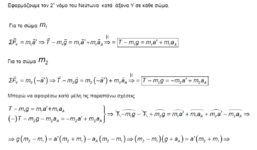 1695377555009.png59,9 KB · Εμφανίσεις: 229
1695377555009.png59,9 KB · Εμφανίσεις: 229 -
 1695377582421.png77,9 KB · Εμφανίσεις: 220
1695377582421.png77,9 KB · Εμφανίσεις: 220 -
 1695377612678.png44,6 KB · Εμφανίσεις: 219
1695377612678.png44,6 KB · Εμφανίσεις: 219
ιωαννηs
Επιφανές μέλος
Ο ιωαννηs αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 15.422 μηνύματα.

23-09-23

01:00
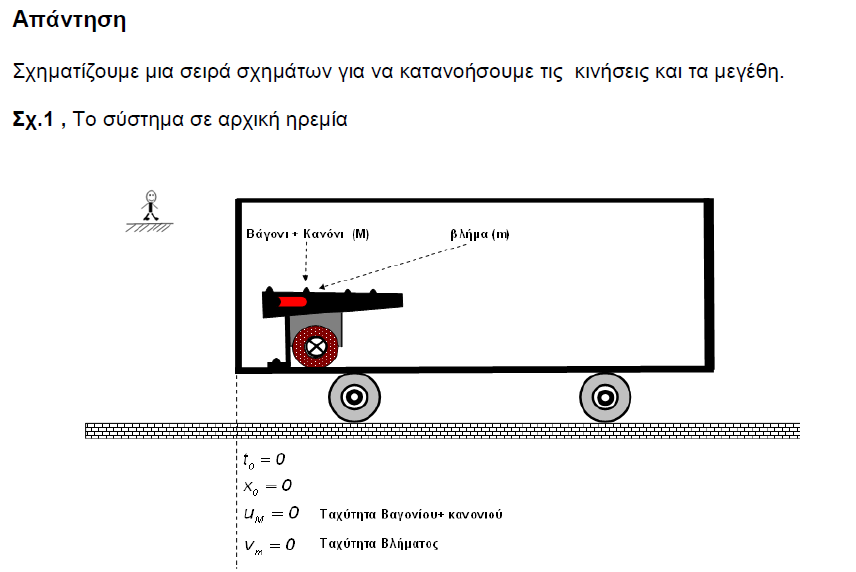
Μια ασκηση Νετωνιας κινηματικης που ξετυλίγει την λογικη των μετασχηματισμων του Γαλιλαιου


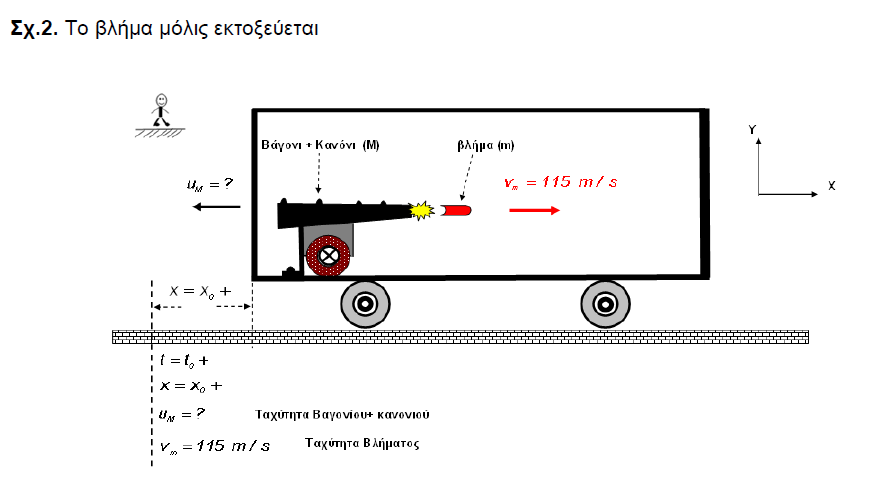

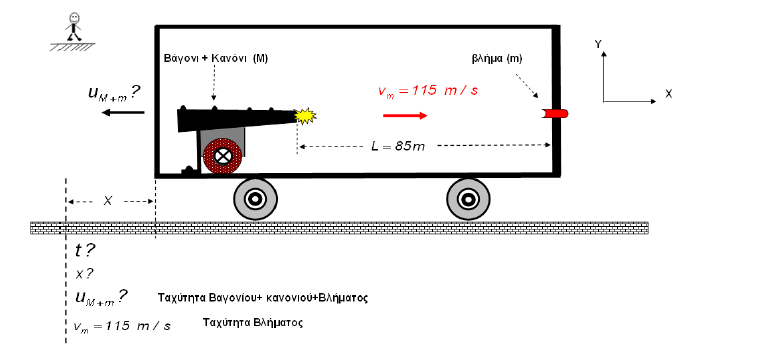

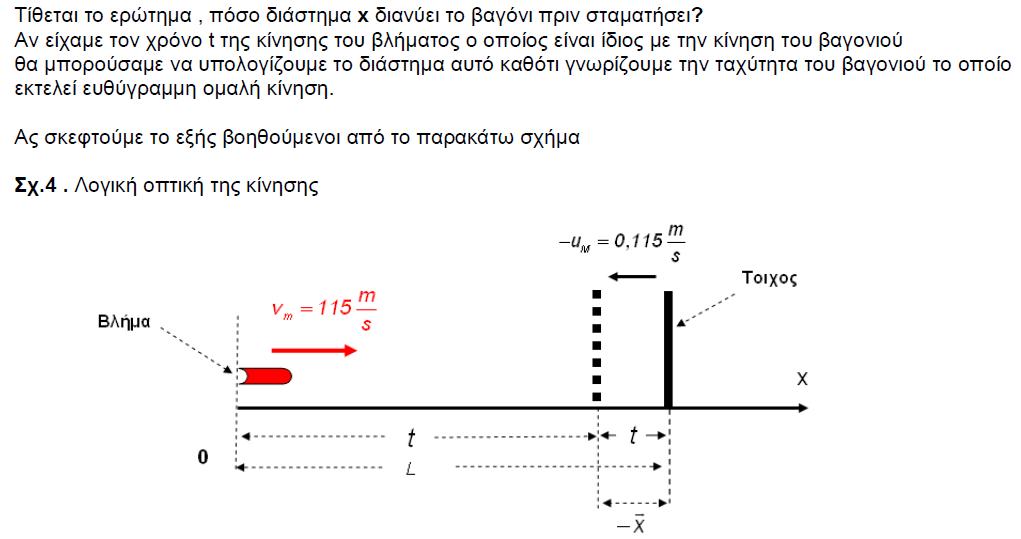
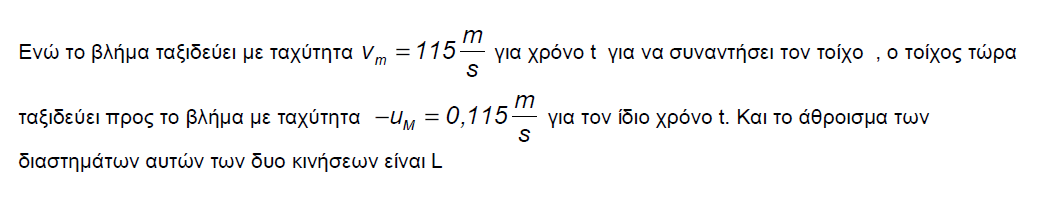

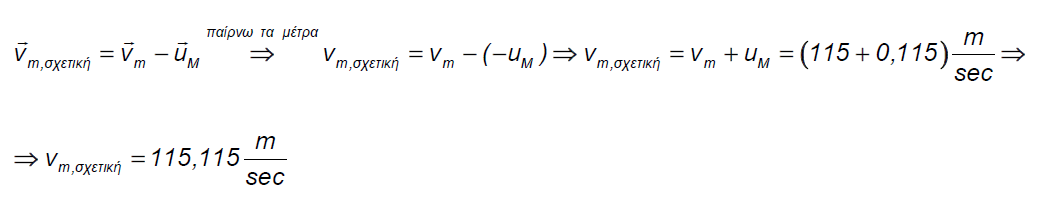

Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.124 μηνύματα.

23-09-23

02:53
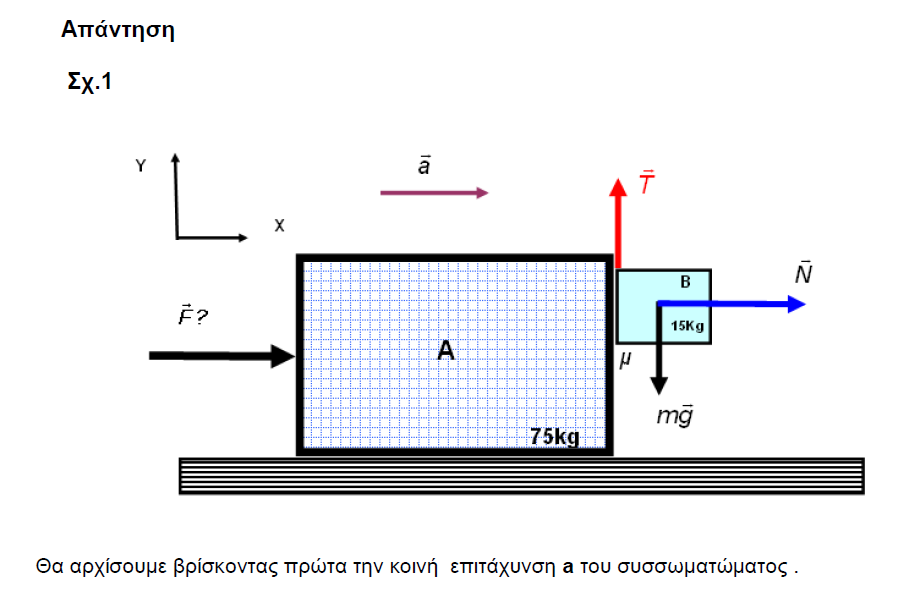
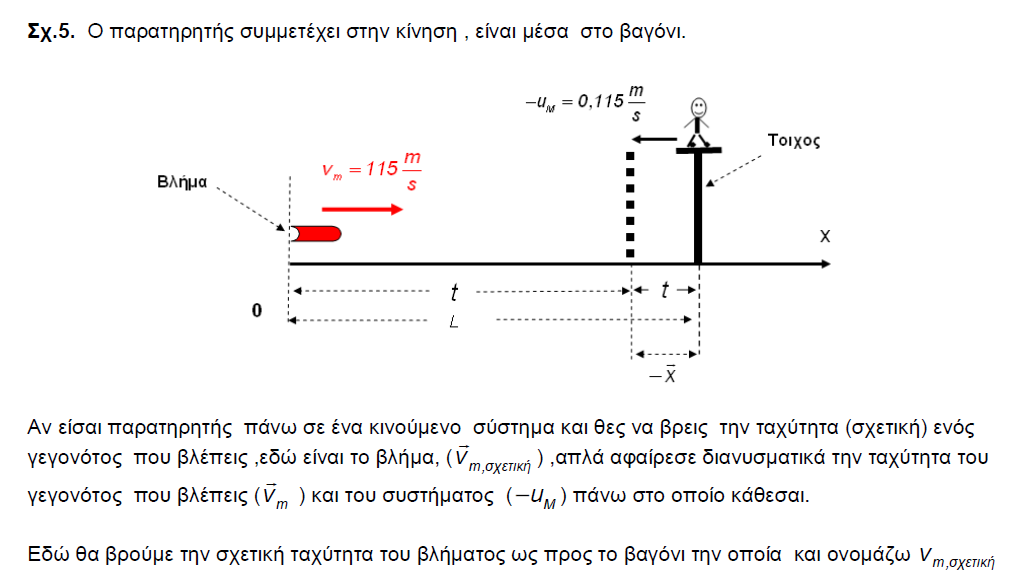
Πρόβλημα :
Δύο καθρέφτες με ανακλαστικότητες R1 και R2 τοποθετούνται σε απόσταση d μεταξύ τους , ο ένας αριστερά και ο άλλος δεξιά ( ο ένας "κοιτάει" τον άλλο στην ουσία ) . Φως έντασης Ιο προσπίπτει στον αριστερό καθρέφτη ανακλαστικότητας R1 . Ποια είναι η ένταση του φωτός που εξέρχεται στα δεξιά του καθρέφτη ανακλαστικότητας R2 ;
Δύο καθρέφτες με ανακλαστικότητες R1 και R2 τοποθετούνται σε απόσταση d μεταξύ τους , ο ένας αριστερά και ο άλλος δεξιά ( ο ένας "κοιτάει" τον άλλο στην ουσία ) . Φως έντασης Ιο προσπίπτει στον αριστερό καθρέφτη ανακλαστικότητας R1 . Ποια είναι η ένταση του φωτός που εξέρχεται στα δεξιά του καθρέφτη ανακλαστικότητας R2 ;
ιωαννηs
Επιφανές μέλος
Ο ιωαννηs αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 15.422 μηνύματα.

23-09-23

21:00
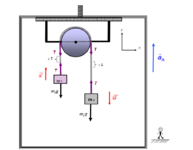
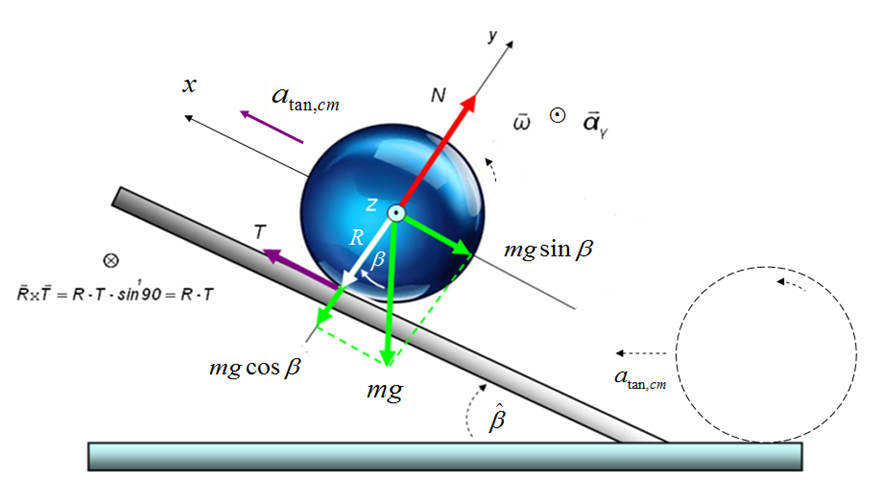
Εδω εχουμε μια μπαλα σε κεκλιμενο επιπεδο..Οκ αντι να το κατεβαινει το ανεβαινει...αλλα το αξιοσημείωτο και παραξενο ειναι οτι η τριβη εχει φορα προς την κατευθυνση της κινησης..





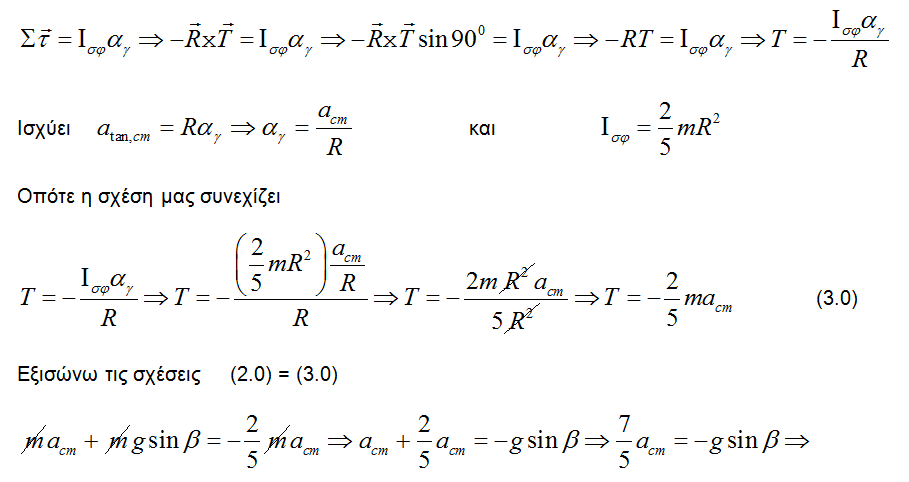




41%
Εκκολαπτόμενο μέλος
Ο 41% αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών και Μαθητής Δημοτικού. Έχει γράψει 250 μηνύματα.

24-09-23

10:30
as i promise@γιαννης_00
Αφιερωμένη σε εσένα,
φτιαγμένη από εμένα με αγάπη.
Έστω πλέγμα 2ν χ (2μ+1) με ν,μ φυσικοί. Τοποθετούμε το πλέγμα 2ν στον άξονα y και το 2μ+1 στον άξονα x. Ξεκινάμε από το τετράγωνο (1,1) και μετακινούμαστε (πάνω, κάτω, αριστερά, δεξιά), από το κάθε τετράγωνο μπορούμε να περάσουμε μόνο μία φορά. Μπορούμε περνώντας από όλα τα τετράγωνα να βρεθούμε στη θέση (2μ+1,1);
Παίξε το με μικρούς αριθμούς στο χαρτίΤσέκαρε την αρχή του χρωματισμού
Υ.Γ. Αν δεν λυθεί εντός βδομάδας θα ανεβάσω τη λύση, αν και αξίζει να ασχοληθείτε.
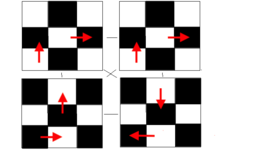
Αρχικά χρωματίζουμε το πλέγμα σε μορφή σκακιέρας (μπορούμε να κάνουμε άπειρους χρωματισμούς, επιλέξαμε αυτόν γιατί μας εξυπηρετεί στο συγκεκριμένο πρόβλημα και πιο συγκεκριμένα επειδή θα παίξουμε με άρτιους-περιττούς). Πλέον παρατηρούμε ότι μπορούμε να πάμε μόνο από Μαύρο->Άσπρο και από Άσπρο->Μαύρο (άρα για να καταλήξουμε σε άσπρο θα χρειαστούμε άρτιο αριθμό κινήσεων ενώ για να καταλήξουμε σε μαύρο θα χρειαστούμε περιττό). Το πλέγμα είναι 2ν χ (2μ + 1) άρα έχει άρτιο αριθμό τετραγώνων. Ξεκινάμε από τη θέση (1,1) που ορίζουμε μαύρο και θέλουμε να καταλήξουμε στη θέση (2μ+1,1) όπου αναγκαστικά θα είναι μαύρο επειδή 2μ+1 θέσεις. Άρα δεν είναι δυνατό να συμβεί αυτό καθώς για να περάσουμε από όλα τα τετράγωνα θα κάνουμε άρτιο αριθμό κινήσεων οπότε το τελευταίο τετράγωνο δεν γίνεται να έχει μαύρο χρωματισμό.
ιωαννηs
Επιφανές μέλος
Ο ιωαννηs αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 15.422 μηνύματα.

24-09-23

10:58
Ευγε νεε, μου ευγε ,,,ωραιο το σκακι... δυστηχως ποτε δεν ασχοληθηκα.
Εχουμε και εμεις κατι τετοια θεματα με διανυσματα οπου βρισκουμε γραφικα αν το πεδιο ειναι στροβιλο ή αστροβιλο..
Ωραιες εποχες δημιουργικες
Εχουμε και εμεις κατι τετοια θεματα με διανυσματα οπου βρισκουμε γραφικα αν το πεδιο ειναι στροβιλο ή αστροβιλο..
Ωραιες εποχες δημιουργικες
41%
Εκκολαπτόμενο μέλος
Ο 41% αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών και Μαθητής Δημοτικού. Έχει γράψει 250 μηνύματα.

24-09-23

11:11
αυτά είναι διαφορετικά που λες και είναι τώρα ωρε, στον ηλεκτρομαγνητισμό. Εκτός αν τελειώνεις ή αν δεν τα έπιασες τόσο σε βάθος μιας και κακά τα ψέματα στο πανεπιστήμιο δεν αναφέρονται τόσο έως καθόλου. Το πρόβλημα που έφτιαξα ήταν διακριτά μαθηματικά άλλη φάση. Ελπίζω να σάρεσεΕχουμε και εμεις κατι τετοια θεματα με διανυσματα οπου βρισκουμε γραφικα αν το πεδιο ειναι στροβιλο ή αστροβιλο..
Ωραιες εποχες δημιουργικες
ιωαννηs
Επιφανές μέλος
Ο ιωαννηs αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 15.422 μηνύματα.

24-09-23

11:17
με αρεσε πολυ...εμεις τα διακριτα μαθηματικα τα εχουμε για τους κομπιουτεραδες δεν τα αγγιζουμε.αυτά είναι διαφορετικά που λες και είναι τώρα ωρε, στον ηλεκτρομαγνητισμό. Εκτός αν τελειώνεις ή αν δεν τα έπιασες τόσο σε βάθος μιας και κακά τα ψέματα στο πανεπιστήμιο δεν αναφέρονται τόσο έως καθόλου. Το πρόβλημα που έφτιαξα ήταν διακριτά μαθηματικά άλλη φάση. Ελπίζω να σάρεσε
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.124 μηνύματα.

24-09-23

13:53
Πως τα εμπλέξες ρε'συ αυτά τα δύο δεν έχουν καμία σχέση αυτά τα δύοΕυγε νεε, μου ευγε ,,,ωραιο το σκακι... δυστηχως ποτε δεν ασχοληθηκα.
Εχουμε και εμεις κατι τετοια θεματα με διανυσματα οπου βρισκουμε γραφικα αν το πεδιο ειναι στροβιλο ή αστροβιλο..
Ωραιες εποχες δημιουργικες

Εγώ σκεφτόμουν τώρα κάτι αλλά δεν ξέρω εάν στέκει . Εάν θεωρούσαμε συνάρτηση απο το Ν* στο Ν^2 με Df = [1, 2ν(2μ +1)] και f(1) = (1,1) , f( 2ν(2μ+1) ) = (2μ+1,1) και δείχναμε ότι δεν μπορεί να είναι 1-1 .
41%
Εκκολαπτόμενο μέλος
Ο 41% αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών και Μαθητής Δημοτικού. Έχει γράψει 250 μηνύματα.

24-09-23

16:16
για κάθε αρχέτυπο υπάρχει μοναδική εικόνα άρα είναι 1-1 και μάλιστα για να το πάμε ένα βήμα παραπέρα είναι διακριτήΕγώ σκεφτόμουν τώρα κάτι αλλά δεν ξέρω εάν στέκει . Εάν θεωρούσαμε συνάρτηση απο το Ν* στο Ν^2 με Df = [1, 2ν(2μ +1)] και f(1) = (1,1) , f( 2ν(2μ+1) ) = (2μ+1,1) και δείχναμε ότι δεν μπορεί να είναι 1-1 .
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.124 μηνύματα.

24-09-23

16:19
Δεν νομίζω οτι γίνεται να είναι 1-1, διότι αυτό , εαν δεν έχω κάνει κάποιο λάθος , θα σήμαινε οτι μπορείς να επισκεπτείς όλα τα τετράγωνα ( ξεκινώντας απο το (1,1) ) και να καταλήξεις στο (2μ+1,1) , χωρίς να περάσεις απο το ίδιο τετράγωνο πάνω απο μια φορά .για κάθε αρχέτυπο υπάρχει μοναδική εικόνα άρα είναι 1-1 και μάλιστα για να το πάμε ένα βήμα παραπέρα είναι διακριτή
41%
Εκκολαπτόμενο μέλος
Ο 41% αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών και Μαθητής Δημοτικού. Έχει γράψει 250 μηνύματα.

24-09-23

16:25
Αν ήταν αύξουσα ή φθίνουσα αυτή η 1-1 δεν είναι τίποτα από τα 2 ίσως εκεί μπερδεύτηκες. Έκτος αν έχεις σκεφτεί κάτι διαφορετικό και δεν το κατανοώ εγώ σωστά.Δεν νομίζω οτι γίνεται να είναι 1-1, διότι αυτό , εαν δεν έχω κάνει κάποιο λάθος , θα σήμαινε οτι μπορείς να επισκεπτείς όλα τα τετράγωνα ( ξεκινώντας απο το (1,1) ) και να καταλήξεις στο (1,2μ+1) , χωρίς να περάσεις απο το ίδιο τετράγωνο πάνω απο μια φορά .
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.124 μηνύματα.

24-09-23

16:34
Ναι περίμενε να σου πω την ιδέα μου γιατί δεν μπορείς να μυρίσεις και εσύ τα νύχια σου .Αν ήταν αύξουσα ή φθίνουσα αυτή η 1-1 δεν είναι τίποτα από τα 2 ίσως εκεί μπερδεύτηκες. Έκτος αν έχεις σκεφτεί κάτι διαφορετικό και δεν το κατανοώ εγώ σωστά.
Σκέφτηκα λοιπόν ως εξής :
Έχουμε συνολικά s = 2ν(2μ+1) τετράγωνα εφόσον το πλέγμα είναι (2ν) X (2μ+1) . Μπορούμε να σκεφτούμε οτι σε κάθε βήμα i που κάνουμε επισκεπτόμαστε ένα τετράγωνο . Άρα χρειαζόμαστε συνολικά s βήματα για να καλύψουμε όλα τα τετράγωνα .
Αν σκεφτούμε λοιπόν πως αντιστοιχούμε σε κάθε φυσικό αριθμό : 1,2,3...,s , που δείχνει σε ποιο βήμα είμαστε , το τετράγωνο (x,y) που έχουμε επισκεπτεί , τότε μπορούμε να ορίσουμε μια συνάρτηση η οποία έχει :
f(1) = (1,1) -> Δείχνει που ξεκινάμε
f(s) = (2μ+1,1) -> Δείχνει που πρέπει να καταλήγουμε στο τελευταίο βήμα .
Η απαίτηση να περάσουμε απο κάθε τετράγωνο μόνο μια φορά ερμηνεύεται ως απαίτηση η f να είναι 1-1 .
Αυτό που παρατηρώ όμως τώρα που το σκέφτομαι καλύτερα είναι οτι δεν ενσωματώνω κάπως τον περιορισμό οτι δεν επιτρέπονται διαγώνια βήματα . Ενδεχομένως να είναι πολύ περίπλοκο να βρεθεί κάποια λύση με το παραπάνω σκεπτικό .
41%
Εκκολαπτόμενο μέλος
Ο 41% αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών και Μαθητής Δημοτικού. Έχει γράψει 250 μηνύματα.

24-09-23

16:42
Ένα προβληματάκι που σκαρφίστηκα μπροστά στα κύματα της θάλασσας, αυτό το αφιερώνω στο φίλο @Samael που άρχισε αυτό το όμορφο thread.
Ένα κουνελάκι βρίσκεται σε μια θέση. Το κουνελάκι μπορεί να κάνει ν κινήσεις (βόρεια, νότια, ανατολικά, δυτικά) όπου ν φυσικός αριθμός. Η κάθε κίνηση είναι 2^ν βήματα. Ξεκινώντας από το 0 μέχρι το ν θα μπορέσει το κουνελάκι να βρεθεί στο μέρος όπου ξεκίνησε; (υποθέτουμε τα βήματα είναι ίσα μεταξύ τους)
Αυτή τη φορά δεν θα ανεβάσω λύση(τουλάχιστον σύντομα) αλλά ίσως γράψω την ιστορία πίσω από τη σύλληψη της(αφού λυθεί).
Ένα κουνελάκι βρίσκεται σε μια θέση. Το κουνελάκι μπορεί να κάνει ν κινήσεις (βόρεια, νότια, ανατολικά, δυτικά) όπου ν φυσικός αριθμός. Η κάθε κίνηση είναι 2^ν βήματα. Ξεκινώντας από το 0 μέχρι το ν θα μπορέσει το κουνελάκι να βρεθεί στο μέρος όπου ξεκίνησε; (υποθέτουμε τα βήματα είναι ίσα μεταξύ τους)
Αυτή τη φορά δεν θα ανεβάσω λύση(τουλάχιστον σύντομα) αλλά ίσως γράψω την ιστορία πίσω από τη σύλληψη της(αφού λυθεί).
Guest 691153
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

24-09-23

16:58
Άσχετο αλλά heres my 2 cents: ευχαριστώ οποιον εφτιαξε αυτο το νημα και όποιους συμβάλλουν, με προβληματα φυσικης, μαθηματικα κλπ. Για λίγο ειχα αποθαρρυνθεί απο τις θετικές επιστήμες αλλα αυτό εδω το θρέντ μου ξαναξύπνησε το ενδιαφέρον, αν και δεν καταλαβαίνω τιποτα, μου αρέσει να βλέπω και ελπίζω κάποια στιγμή να μπορώ να στείλω και γω κάτι
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 278 μέλη διάβασαν αυτό το θέμα:
- Cocobolo
- Salomon Jonas
- many of Filip
- ChrisG152
- ether--net
- Hased Babis
- GNick06
- Marildrea
- globglogabgalab
- Georgiaaa_
- Bonaparte
- Ilias__
- Kabamaru Hayate
- panosalex7
- eukleidhs1821
- SlimShady
- jYanniss
- Drscientist
- Corfu kitty
- bak07
- Kate1914
- aris65
- jellojina
- Unboxholics
- sakplat
- Chrisphys
- bigguy
- love_to_learn
- tsiobieman
- Wonderkid
- Tolis211
- suaimhneas
- Indecisive2
- bibliofagos
- Hecticism
- ggl
- panosT436
- rseven
- Debugging_Demon
- andromaxh07
- Scandal
- georgetherrr
- antonis97
- BatGuin
- thesmilingchild
- iiTzArismaltor_
- Μήτσος10
- Orfano
- charmander
- eirinipap
- exotic xo
- Giorgosvr
- Qwerty 0
- Than003
- angela_k
- Jomo
- Joji
- kost28
- redpointer
- Albert.123
- Leo komm
- P.Dam.
- Steliosgkougkou
- chjan
- Evangeloz
- wmaria
- Maynard
- χημεια4λαιφ
- donut_daddy
- marikakitsou16
- physicscrazy
- Lia 2006
- chester20080
- panaman
- Msp1
- Sotis
- mirara
- melver
- grad778
- nickd
- V@Per
- ssalex
- catlover033
- carnage
- Μιχαήλ
- vas2017
- beatrixx
- phleidhs
- gegeorgiou90
- Dr. Gl. Luminous
- agg41
- thepigod762
- Helen06
- math2arch
- MrDragonboy
- chrismpd
- bill09876
- Paragontas7000
- ikigai
- Marel
- soleilst
- Startx0
- marilenaaa
- EllieKal
- gzois
- EFAKIT
- Φινεύς
- estrela
- Lifelong Learner
- Annie
- Panatha mono
- Mitsaras23
- Isa
- BiteTheDust
- Chris180
- aplalew
- user111
- Chemwizard
- giannhs2001
- Mukumbura
- MR WHITE
- SIAmia
- supertom4000
- J.Cameron
- persour
- Totreno
- sotirislk
- Specon
- Mariosm.
- Claire05
- Giorgos216
- Jimpower
- shezza94
- kwstasloul
- kan3nas
- dmav
- Obi-Wan Kenobi
- Nancysmilkyway
- Νομάρχης
- ogigidi
- ένας τυχαίος
- Hmmytheos
- constansn
- cannot_log_in
- hello1234
- ilal1200
- Alessandra Eliza
- Giannis327
- phoni
- aggorf
- Nala
- Frozensun
- xrisamikol
- Ilovemycats27
- PanosApo
- nik64
- angies
- dimitris_eee
- mike19
- angeloskar
- eltqt
- CrusaderKingsIII
- flaura
- elevag
- Patroklos
- Anonymous1
- IcedBreaje
- kiyoshi
- nicole1982
- Lost_In_Life
- Γατέχων
- AggelikiGr
- Nansytsg
- Lathy
- k4t
- Maria_Xagorari
- suuuuiiii
- SoyN
- thecrazycretan
- Jesse_
- A350
- Ιωάννης1234
- george777
- Abiogenesis
- Enhypen
- Mary06
- arko
- Giorgkalo
- velentzakoss
- Giota_pel
- AnnaRd
- Νικολινα
- NikNik1995
- BillyTheKid
- Nick_nt
- a namaves
- xristarac
- ilovekpop
- GeorgePap2003
- Sofos Gerontas
- topg
- Γιώτα Γιαννακού
- plantbee
- Peter Pan13
- Ness
- MrDna
- Jojo K
- Mewmaw
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



