Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 18 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 515 μηνύματα.

24-08-23

15:23
Γειά σας, μπορεί κάποιος να βοηθήσει σ'αυτήν την ανίσωση;
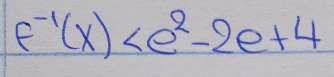
Σε περίπτωση που χρειαστεί αυτή είναι η δοσμένη σχέση, ωστόσο σ'αυτήν ζητάει και να βρω το πεδίο ορισμού, η ερώτησή μου για το π.ο είναι το ριζα(χ-3) +1 >0 ισχύει πάντα; δηλαδή θα ήταν λάθος αν πάω το 1 στο 2ο μέλος υψώσω στο τετράγωνο κλπ;
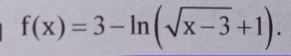
Σε περίπτωση που χρειαστεί αυτή είναι η δοσμένη σχέση, ωστόσο σ'αυτήν ζητάει και να βρω το πεδίο ορισμού, η ερώτησή μου για το π.ο είναι το ριζα(χ-3) +1 >0 ισχύει πάντα; δηλαδή θα ήταν λάθος αν πάω το 1 στο 2ο μέλος υψώσω στο τετράγωνο κλπ;
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

24-08-23

15:41
Βρες την f^-1 από την f, σκέψου τι συνήθως κάνουμε σε τέτοιου είδους ανισώσεις. Πρέπει το χ-3 να είναι μη αρνητικό αφού είναι κάτω από το υπόρριζο. Επειδή οι ρίζες είναι μη αρνητικές, ό,τι είναι εντός του ln είναι θετικό και μάλιστα μεγαλύτερο ή ίσο του 1, έχε το κατά νου στους περιορισμούς που θα πάρεις. Προσπάθησέ την και αν κολλάς και πάλι εδώ είμαστε.Γειά σας, μπορεί κάποιος να βοηθήσει σ'αυτήν την ανίσωση;
View attachment 120387
Σε περίπτωση που χρειαστεί αυτή είναι η δοσμένη σχέση, ωστόσο σ'αυτήν ζητάει και να βρω το πεδίο ορισμού, η ερώτησή μου για το π.ο είναι το ριζα(χ-3) +1 >0 ισχύει πάντα; δηλαδή θα ήταν λάθος αν πάω το 1 στο 2ο μέλος υψώσω στο τετράγωνο κλπ;
View attachment 120388
Το να υψώσεις στο τετράγωνο δεν είναι σωστό. Για παράδειγμα, -1<0 δεν σημαίνει ότι (-1)^2<0^2 δηλαδή 1<0. Υψώνουμε σε άρτια δύναμη μόνο όταν και τα δύο μέλη είναι μη αρνητικά.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

24-08-23

15:45
Γεια σου Ελένη.Γειά σας, μπορεί κάποιος να βοηθήσει σ'αυτήν την ανίσωση;
View attachment 120387
Σε περίπτωση που χρειαστεί αυτή είναι η δοσμένη σχέση, ωστόσο σ'αυτήν ζητάει και να βρω το πεδίο ορισμού, η ερώτησή μου για το π.ο είναι το ριζα(χ-3) +1 >0 ισχύει πάντα; δηλαδή θα ήταν λάθος αν πάω το 1 στο 2ο μέλος υψώσω στο τετράγωνο κλπ;
View attachment 120388
Το πεδίο ορισμού της f είναι το x >= 3 .
Η ρίζα είναι πάντα μη αρνητική , οπότε με + 1 έχεις μια καθαρά θετική ποσότητα στο όρισμα του λογάριθμου . Επομένως για να ορίζεται η συνάρτηση το μόνο που απαιτείται είναι το υπόριζο να είναι θετικό , το οποίο φυσικά σημαίνει το x να είναι >=3 .
Η ln για την ακρίβεια είναι γνησίως αύξουσα συνάρτηση , οπότε η -ln είναι γνησίως φθίνουσα . Το +3 απλά κάνει μια κατακόρυφη μετατόπιση οπότε δεν επηρεάζει την μονοτονία και έτσι η f είναι γνησίως φθίνουσα .
Αυτό μπορείς να το δείξεις εύκολα . Εαν ξέρεις οτι :
g(x) = -f(x) και η f είναι γνησίως αύξουσα , τότε :
x1 < x2 => f γνησίως αύξουσα
f(x1) < f(x2) =>
-f(x1) > -f(x2) =>
g(x1) > g(x2)
Οπότε πράγματι η g είναι γνησίως φθίνουσα .
Στην ανίσωση που έχεις να λύσεις λοιπόν μπορείς να περάσεις f και στα δύο μέλη αξιοποιώντας την μονοτονία της :
f-1(x) < e² -2e +4 => f γνησίως φθίνουσα
f(f-1(x)) > f(e² -2e +4) =>
x > f(e² -2e +4) =>
x > 3 - ln( sqrt( (e - 1)²) ) + 1) = 3 - ln( e - 1 + 1 ) = 3 - lne = 2
x > 2
Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 18 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 515 μηνύματα.

24-08-23

15:58
x > 3 - ln( sqrt( (e - 1)²) ) + 1) = 3 - ln( e - 1 + 1 ) = 3 - lne = 2
x > 2
 λίγο με έχασες εδώ, μέχρι τα πιο πάνω οκ, αρχικά και εγώ μέχρι εκεί τα έφτασα αλλα εδώ τι εννοεις;
λίγο με έχασες εδώ, μέχρι τα πιο πάνω οκ, αρχικά και εγώ μέχρι εκεί τα έφτασα αλλα εδώ τι εννοεις;Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

24-08-23

16:07
Έλα βρε , στο πιο απλό κόλλησες .λίγο με έχασες εδώ, μέχρι τα πιο πάνω οκ, αρχικά και εγώ μέχρι εκεί τα έφτασα αλλα εδώ τι εννοεις;
Πια πάνω καταλήγουμε στην :
x > f(e² -2e +4)
Θεώρησε τον αριθμό :
u = e² -2e + 4
Οπότε :
f(e² -2e + 4) = f(u)
Έτσι :
f(u) = 3 - ln[ sqrt( u - 3 ) + 1 ] =>
f(u) = 3 - ln[ sqrt( e² -2e + 4 - 3 ) + 1 ] =>
f(u) = 3 - ln[ sqrt( e² -2e + 1 ) + 1 ] =>
f(u) = 3 - ln[ sqrt( {e - 1}²) + 1 ] =>
f(u) = 3 - ln[ |e - 1| + 1 ] => e - 1 > 0
f(u) = 3 - ln[ e - 1 + 1 ] =>
f(u) = 3 - ln[ e - 1 + 1 ] =>
f(u) = 3 - lne =>
f(u) = 2 =>
f(e² -2e + 4) = 2
Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 18 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 515 μηνύματα.

24-08-23

16:12
αααα οκει κατάλααβα, γίνεται πάντως να θέτουμε σε όποιο σημείο μας βολεύει για να συνεχίσουμε γιατί το έκανα και σε μία άλλη άσκηση με λίγη αμφιβολία. Παρόλα αυτά σ'ευχαριστώ πολύ για τον χρόνο σου!Έλα βρε , στο πιο απλό κόλλησες .
Πια πάνω καταλήγουμε στην :
x > f(e² -2e +4)
Θεώρησε τον αριθμό :
u = e² -2e + 4
Οπότε :
f(e² -2e + 4) = f(u)
Έτσι :
f(u) = 3 - ln[ sqrt( u - 3 ) + 1 ] =>
f(u) = 3 - ln[ sqrt( e² -2e + 4 - 3 ) + 1 ] =>
f(u) = 3 - ln[ sqrt( e² -2e + 1 ) + 1 ] =>
f(u) = 3 - ln[ sqrt( {e - 1}²) + 1 ] =>
f(u) = 3 - ln[ |e - 1| + 1 ] => e - 1 > 0
f(u) = 3 - ln[ e - 1 + 1 ] =>
f(u) = 3 - ln[ e - 1 + 1 ] =>
f(u) = 3 - lne =>
f(u) = 2 =>
f(e² -2e + 4) = 2
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Τέλεια ναι! Σ'ευχαριστώΤο να υψώσεις στο τετράγωνο δεν είναι σωστό. Για παράδειγμα, -1<0 δεν σημαίνει ότι (-1)^2<0^2 δηλαδή 1<0. Υψώνουμε σε άρτια δύναμη μόνο όταν και τα δύο μέλη είναι μη αρνητικά.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

24-08-23

16:34
Θέτε όπου μπορείς εαν πιστεύεις οτι βελτιώνει την αισθητική του γραπτού σου ή όταν διευκολύνει/μειώνει το γράψιμο . Μπορεί επιπλέον να αποτελέσει σημαντικό βοήθημα για να δεις πιο ξεκάθαρα ορισμένα πράγματα .αααα οκει κατάλααβα, γίνεται πάντως να θέτουμε σε όποιο σημείο μας βολεύει για να συνεχίσουμε γιατί το έκανα και σε μία άλλη άσκηση με λίγη αμφιβολία. Παρόλα αυτά σ'ευχαριστώ πολύ για τον χρόνο σου!
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Τέλεια ναι! Σ'ευχαριστώ
Σχετικά με την ερώτηση για το τετράγωνο...να σημειώσω οτι μπορείς να υψώσεις σε δύναμη εαν ξέρεις οτι και τα δύο μέλη είναι μη αρνητικά ή εαν ξέρεις οτι είναι και τα δύο αρνητικά . Λόγου χάρη :
Αν 0 <= x < y , τότε : x² < y²
Αν y < x <= 0 , τότε : x² < y²
Αν ισχύει x < 0 < y , τότε δεν μπορείς να αποφανθείς τι ισχύει για τα τετράγωνα εκτός εαν έχεις γνώση σχετικά με τις απόλυτες τιμές τους ή αν διακρίνεις περιπτώσεις :
Aν |χ| > |y| :
|χ| - |y| > 0 =>
(|χ| - |y|)(|χ| + |y|) > 0 *
|χ|² - |y|² > 0
χ² > y²
Με παρόμοιο τρόπο αποδεικνύεις οτι αν |χ| < |y| :
χ² < y²
*|χ| + |y| > 0 , εφόσον |α| >= 0 , με |α| = 0 μόνο αν α = 0 , και x,y != 0
Καλό διάβασμα
Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 18 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 515 μηνύματα.

24-08-23

18:03
Πωω Σευχαριστώ πάρα πολυ!!Θέτε όπου μπορείς εαν πιστεύεις οτι βελτιώνει την αισθητική του γραπτού σου ή όταν διευκολύνει/μειώνει το γράψιμο . Μπορεί επιπλέον να αποτελέσει σημαντικό βοήθημα για να δεις πιο ξεκάθαρα ορισμένα πράγματα .
Σχετικά με την ερώτηση για το τετράγωνο...να σημειώσω οτι μπορείς να υψώσεις σε δύναμη εαν ξέρεις οτι και τα δύο μέλη είναι μη αρνητικά ή εαν ξέρεις οτι είναι και τα δύο αρνητικά . Λόγου χάρη :
Αν 0 <= x < y , τότε : x² < y²
Αν y < x <= 0 , τότε : x² < y²
Αν ισχύει x < 0 < y , τότε δεν μπορείς να αποφανθείς τι ισχύει για τα τετράγωνα εκτός εαν έχεις γνώση σχετικά με τις απόλυτες τιμές τους ή αν διακρίνεις περιπτώσεις :
Aν |χ| > |y| :
|χ| - |y| > 0 =>
(|χ| - |y|)(|χ| + |y|) > 0 *
|χ|² - |y|² > 0
χ² > y²
Με παρόμοιο τρόπο αποδεικνύεις οτι αν |χ| < |y| :
χ² < y²
*|χ| + |y| > 0 , εφόσον |α| >= 0 , με |α| = 0 μόνο αν α = 0 , και x,y != 0
Καλό διάβασμα
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

24-08-23

18:30
Αν η f είναι η ίδια, όχι, δεν μπορείς να περάσεις f σε πρώτη φάση γιατί το πεδίο ορισμού της είναι το [3,+oo).View attachment 120399 Γίνεται να την λύσω έτσι: f(f-1(e^f(x)-1)=f(0)<=>e^f(x)-1=f(0) και μετα στη θέση του 0 να βάλω το f-1(0) για να βγει και να μείνει 0;
Αν μπορούσες, θα έπρεπε να ισχύει f^-1(0)=0 για να κάνεις την αντικατάσταση που λες (δεν ισχύει εν προκειμένω).
Επειδή φαντάζομαι ότι η f είναι ίδια, η άσκηση λύνεται κανονικά, σκέψου πιο πονηρά. Μελέτησε την f^-1...δες τι σου έγραψα στην αρχή...
Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 18 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 515 μηνύματα.

24-08-23

18:32
οχι οχι ειναι άλλη άσκηση συγνωμη, η δοσμένη σχέση είναι αυτή f(f(x))-f(x)=-xΑν η f είναι η ίδια, όχι, δεν μπορείς να περάσεις f σε πρώτη φάση γιατί το πεδίο ορισμού της είναι το [3,+oo).
Αν μπορούσες, θα έπρεπε να ισχύει f^-1(0)=0 για να κάνεις την αντικατάσταση που λες.
Επειδή φαντάζομαι ότι η f είναι ίδια, η άσκηση λύνεται, σκέψου πιο πονηρά. Μελέτησε την f^-1...
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

24-08-23

18:43
Σωστή , αλλά δεν υπάρχει λόγος να αντικαταστήσεις το 0 με f-1(0) εφόσον ξέρεις οτι f(0) = 0οχι οχι ειναι άλλη άσκηση συγνωμη, η δοσμένη σχέση είναι αυτή f(f(x))-f(x)=-x
 .
.Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

24-08-23

18:44
Ααααααα ΟΚ. Πάντως έβγαινε και στο άλλο καλό θέμα.οχι οχι ειναι άλλη άσκηση συγνωμη, η δοσμένη σχέση είναι αυτή f(f(x))-f(x)=-x

Φαντάζομαι για κάθε x που ανήκει στους πραγματικούς η σχέση και έβγαλες ότι είναι 1-1.
Λοιπόν, ό,τι σου είπα και πριν. Το πρώτο βήμα είναι ΟΚ, μην μπλέξεις μετά, βρες πόσο κάνει το f(0), εύκολο από 1-1 (που μάλλον το έκανες αν καταλαβαίνω καλά). Αν και σωστή είναι η αντικατάστασή σου. Στο λέω μπαίνοντας στο μυαλό αυτών που διορθώνουν, δεν θέλουν να βλέπουν πλάγιες μεθόδους αρκετοί εξ' αυτών. Κακώς βέβαια, αλλά έτσι συμβαίνει.
Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 18 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 515 μηνύματα.

24-08-23

18:50
Α οντως ισχυει; ουπς (δεν κάναμε πάντως παράγωγο αν τυχαία είναι σ'εκείνη την ενότητα)f(0) = 0
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
ναι το ζητούσε και στο α ερώτημα της άσκησης αλλα πως βρίσκω απο 1-1 πόσο κάνει το f(0)Το πρώτο βήμα είναι ΟΚ, μην μπλέξεις μετά, βρες πόσο κάνει το f(0), εύκολο από 1-1 (που μάλλον το έκανες αν καταλαβαίνω καλά).
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

24-08-23

18:55
Φαντάζομαι απέδειξες οτι είναι 1-1 , δεν είναι δύσκολο με τον ορισμό .Α οντως ισχυει; ουπς
Απο εκεί και πέρα εαν βάλεις όπου χ το 0 :
f(f(x)) - f(x)= -x =>
f(f(0)) = f(0) => επειδή η f είναι 1-1 όμως
f(0) = 0
Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 18 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 515 μηνύματα.

24-08-23

18:56
αα ναι ειμαι χαζήΦαντάζομαι απέδειξες οτι είναι 1-1 δεν είναι δύσκολο με τον ορισμό .
Απο εκεί και πέρα εαν έβαλες όπου χ το 0 :
f(f(x))-f(x)=-x
f(f(0)) = f(0) => επειδή η f : 1-1
f(0) = 0
 Ευχαριστώ και τους δυο σας!!
Ευχαριστώ και τους δυο σας!!Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

24-08-23

19:01
Χαρά μας .αα ναι ειμαι χαζήΕυχαριστώ και τους δυο σας!!
Practice makes perfect girl
 . Συνέχισε και θα γίνεσαι ολοένα και καλύτερη
. Συνέχισε και θα γίνεσαι ολοένα και καλύτερη  .
.Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

24-08-23

19:03
Όπως σου είπε ο @Samael.ναι το ζητούσε και στο α ερώτημα της άσκησης αλλα πως βρίσκω απο 1-1 πόσο κάνει το f(0)
Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 18 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 515 μηνύματα.

24-08-23

20:31
Μια τελευταία ερω΄τηση
 Έκανα τιςσ πράξεις και κατέληξα στο f(x)=0 γίνεται να πω ότι θέτω χ =f-1(x);
Έκανα τιςσ πράξεις και κατέληξα στο f(x)=0 γίνεται να πω ότι θέτω χ =f-1(x);Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

24-08-23

20:51
Μωρέ κάνε όσες θες , δεν έχει όριοΜια τελευταία ερω΄τησηΈκανα τιςσ πράξεις και κατέληξα στο f(x)=0 γίνεται να πω ότι θέτω χ =f-1(x);
 .
.Πιστεύω ότι ο πιο κατάλληλος τρόπος θα ήταν να πεις πως εφόσον f(0) = 0 η εξίσωση γράφεται :
f(x) = f(0)
Η f όμως είναι 1-1 , άρα η εξίσωση έχει μοναδική λύση το x = 0 .
Ο τρόπος που προτείνεις δεν είναι σωστός διότι τι θα γινόταν εάν η f δεν μηδενιζοταν στο x = 0 ; Αυτή η αντικατάσταση επιβάλει οτι η f μηδενίζεται απαραίτητα στο 0 , το οποίο δεν είναι υποχρεωτικό για μια τυχούσα αντιστρέψιμη συνάρτηση .
Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 18 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 515 μηνύματα.

24-08-23

20:53
AX NAIII θεε μου τι εχω παθειΠιστεύω ότι ο πιο κατάλληλος τρόπος θα ήταν να πεις πως εφόσον f(0) = 0 η εξίσωση γράφεται :
f(x) = f(0)
Η f όμως είμαι 1-1 , άρα η εξίσωση έχει μοναδική λύση το x = 0 .
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 4 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 59 μέλη διάβασαν αυτό το θέμα:
- Mariosm.
- shezza94
- Mary06
- topg
- Hmmytheos
- Hased Babis
- giannis05
- Leo komm
- Panagiotis849
- suaimhneas
- MrDna
- angies
- eukleidhs1821
- Helen06
- ggl
- Alessandra Eliza
- Ness
- Maynard
- arapakos
- Scandal
- Wonderkid
- suuuuiiii
- iiTzArismaltor_
- GeorgePap2003
- Frozensun
- Ιωάννα λ
- Magigi
- Γατέχων
- Giannis_19
- AggelikiGr
- Joji
- guest24440
- Lifelong Learner
- Γιώτα Γιαννακού
- Unboxholics
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

