Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

04-09-22

20:31
Έχω δει γενικό τύπο.μπορούμε να βγάλουμε και γενικό τύπο σωστά ;
ενδιαφέρον θα χε
Oof
Εκκολαπτόμενο μέλος
Ο Oof αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 20 ετών και Φοιτητής του τμήματος Ναυπηγών Μηχανολόγων Μηχανικών ΕΜΠ. Έχει γράψει 267 μηνύματα.

04-09-22

20:33
Με λίγο ψάξιμο στο quora βρήκα αυτό : n/2^(n-1) που όντως για 3 σημεία δίνει 3/4 και για 4 1/2Έχω δει γενικό τύπο.
Το derivation του τύπου δε το έπιασα οποίος το καταλάβει ας γράψει εδώ
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

04-09-22

20:35
@Andypro
Το πήγα με μέγιστες αποστάσεις τόξων. Αν θεωρήσουμε το κάθε σημείο ως άκρο τότε παίρνουμε ένα θεωρητικό τόξο που το έχει ως άκρο και βρίσκουμε τα σημεία στα οποία αν παίξει το τρίτο σημείο θα είναι εντός του τόξου που θέλουμε. Κάνουμε την διαδικασία αυτή και για τα δύο σημεία. Επειδή τα δύο πρώτα σημεία που θα επιλέξουμε κατά μέσο όρο βρίσκονται 90 μοίρες μακριά, θα καλύπτουν τα θεωρητικά τόξα 270 μοίρες, άρα και 3/4 η πιθανότητα που και εσύ μας είπες.
Δεν θα μπορούσα να σκεφτώ έτσι και για το 4ο; Σόρρυ αν λέω βλακείες αλλά δεν έχω ασχοληθεί με πιθανότητες.
Το πήγα με μέγιστες αποστάσεις τόξων. Αν θεωρήσουμε το κάθε σημείο ως άκρο τότε παίρνουμε ένα θεωρητικό τόξο που το έχει ως άκρο και βρίσκουμε τα σημεία στα οποία αν παίξει το τρίτο σημείο θα είναι εντός του τόξου που θέλουμε. Κάνουμε την διαδικασία αυτή και για τα δύο σημεία. Επειδή τα δύο πρώτα σημεία που θα επιλέξουμε κατά μέσο όρο βρίσκονται 90 μοίρες μακριά, θα καλύπτουν τα θεωρητικά τόξα 270 μοίρες, άρα και 3/4 η πιθανότητα που και εσύ μας είπες.
Δεν θα μπορούσα να σκεφτώ έτσι και για το 4ο; Σόρρυ αν λέω βλακείες αλλά δεν έχω ασχοληθεί με πιθανότητες.
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

04-09-22

20:39
Αυτό είναι το point πάνω-κάτω. Μπορείς να δεις το σύνολο σημείων ως χώρο (κύκλος x κύκλος x κύκλος x κύκλος) που αποδεκτό είναι ένα υποσύνολο αυτών.@Andypro
Το πήγα με μέγιστες αποστάσεις τόξων. Αν θεωρήσουμε το κάθε σημείο ως άκρο τότε παίρνουμε ένα θεωρητικό τόξο που το έχει ως άκρο και βρισκουμε τα σημεία στα οποία αν παίξει το τρίτο σημείο θα είναι εντός του τόξου που θέλουμε. Κάνουμε την διαδικασία αυτή και για τα δύο σημεία. Επειδή τα δύο πρώτα σημεία που θα επιλέξουμε κατά μέσο όρο βρίσκονται 90 μοίρες μακριά, θα καλύπτουν τα θεωρητικά τόξα 270 μοίρες, άρα και 3/4 η πιθανότητα που και εσύ μας είπες.
Δεν θα μπορούσα να σκεφτώ έτσι και για το 4ο; Σόρρυ αν λέω βλακείες αλλά δεν έχω ασχοληθεί με πιθανότητες.
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

06-09-22

11:06
Λοιπόν, επειδή κι εγώ δεν είδα κάποια λύση που να με ικανοποιεί 100% για το πρόβλημα, θα χρησιμοποιήσω συνεχείς τυχαίες μεταβλητές.
Λέω 2 σημεία διαδοχικά αν δεν παρεμβάλλεται κανένα άλλο μεταξύ τους από τα 4 που μελετά το πρόβλημα.
Ξεκινώντας από 1 από τα σημεία μπορώ να πάω σε οποιοδήποτε διαδοχικό του διαγράφοντας είτε μια θετική είτε μια αρνητική γωνία στο διάστημα [-π, π]. Αποδεκτά αποτελέσματα είναι όσα έχουν άθροισμα απόλυτων τιμών γωνιών μεταξύ διαδοχικών σημείων < π.
Έστω θ η γωνία μεταξύ του πρώτου σημείου και κάποιου διαδοχικού του. Η συνάρτηση πυκνότητας πιθανότητας για την θ είναι f(θ) = 1/2π στο [-π,π]. Έστω Θ = |θ|. f(Θ) = 1/π στο [0,π].
Ομοίως ορίζουμε έτσι τη συνάρτηση για τις άλλες γωνίες μεταξύ διαδοχικών σημείων, έστω ω και φ. Ω = |ω|, Φ = |φ|.
Έστω Γ = Θ + Ω + Φ. Θέλουμε το convolution των 3 αυτών συναρτήσεων. Έπειτα, μπορούμε να εξαγάγουμε την δεσμευμένη πιθανότητα P(Γ < π | Γ < 2π). Επιλέγω τη δεσμευμένη πιθανότητα καθώς οποιοσδήποτε σχηματισμός με άθροισμα των απολύτων των γωνιών > 2π, μπορεί να σχηματιστεί με μικρότερες γωνίες και τα σημεία να είναι ίδια.
Αν Α το σύνολο των αποδεκτών τετράδων και Β το σύνολο όλων των μη αποδεκτών τετράδων τότε παίρνουμε το "ποσοστό"
|Α|/|4Α+4Β|, γιατί κάθε αποδεκτή τετράδα θα μετρηθεί 3 φορές ως μη αποδεκτή.
Λέω 2 σημεία διαδοχικά αν δεν παρεμβάλλεται κανένα άλλο μεταξύ τους από τα 4 που μελετά το πρόβλημα.
Ξεκινώντας από 1 από τα σημεία μπορώ να πάω σε οποιοδήποτε διαδοχικό του διαγράφοντας είτε μια θετική είτε μια αρνητική γωνία στο διάστημα [-π, π]. Αποδεκτά αποτελέσματα είναι όσα έχουν άθροισμα απόλυτων τιμών γωνιών μεταξύ διαδοχικών σημείων < π.
Έστω θ η γωνία μεταξύ του πρώτου σημείου και κάποιου διαδοχικού του. Η συνάρτηση πυκνότητας πιθανότητας για την θ είναι f(θ) = 1/2π στο [-π,π]. Έστω Θ = |θ|. f(Θ) = 1/π στο [0,π].
Ομοίως ορίζουμε έτσι τη συνάρτηση για τις άλλες γωνίες μεταξύ διαδοχικών σημείων, έστω ω και φ. Ω = |ω|, Φ = |φ|.
Έστω Γ = Θ + Ω + Φ. Θέλουμε το convolution των 3 αυτών συναρτήσεων. Έπειτα, μπορούμε να εξαγάγουμε την δεσμευμένη πιθανότητα P(Γ < π | Γ < 2π). Επιλέγω τη δεσμευμένη πιθανότητα καθώς οποιοσδήποτε σχηματισμός με άθροισμα των απολύτων των γωνιών > 2π, μπορεί να σχηματιστεί με μικρότερες γωνίες και τα σημεία να είναι ίδια.
Αν Α το σύνολο των αποδεκτών τετράδων και Β το σύνολο όλων των μη αποδεκτών τετράδων τότε παίρνουμε το "ποσοστό"
|Α|/|4Α+4Β|, γιατί κάθε αποδεκτή τετράδα θα μετρηθεί 3 φορές ως μη αποδεκτή.
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

06-09-22

20:46
Μια καινούργια, ελπίζω πιο βατή.
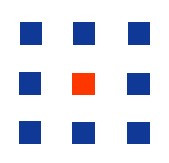
Δημιουργούμε lock patterns αυστηρά σε σχήμα τριγώνου ή ορθ. παραλληλογράμμου με κλίσεις στα ευθύγραμμα τμήματα ίσες με αυτές των καθέτων, των οριζοντίων γραμμών και των 2 διαγωνίων. Ποια είναι η πιθανότητα να συμπεριλαμβάνεται το κέντρο του τετραγώνου στο lock pattern; Τι ισχύει αν, αντί για 3 x 3 διαθέσιμες θέσεις, είναι n x n, n > 1 και περιττός;
Θεωρούμε όλα τα αποδεκτά lock patterns ισοπίθανα.
Δημιουργούμε lock patterns αυστηρά σε σχήμα τριγώνου ή ορθ. παραλληλογράμμου με κλίσεις στα ευθύγραμμα τμήματα ίσες με αυτές των καθέτων, των οριζοντίων γραμμών και των 2 διαγωνίων. Ποια είναι η πιθανότητα να συμπεριλαμβάνεται το κέντρο του τετραγώνου στο lock pattern; Τι ισχύει αν, αντί για 3 x 3 διαθέσιμες θέσεις, είναι n x n, n > 1 και περιττός;
Θεωρούμε όλα τα αποδεκτά lock patterns ισοπίθανα.
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

09-09-22

13:14
Μερικά σχόλια για τη λύση:
Για την περίπτωση που n = 3 η απάντηση είναι:
Για τη γενική περίπτωση:
Χωρίζω τα σχήματα στα εξής σύνολα:

ΥΓ. Στο προηγούμενο μάλλον έπρεπε να βάλω δέσμευση στο 3π/2 και όχι στο 2π.
Για την περίπτωση που n = 3 η απάντηση είναι:
32/38. Μόνο τα 4 ορθογώνια τρίγωνα {(1,1), (1,2), (2,1), (1,1)} κτλ., το λοξό τετράγωνο {(1,2),(2,1),(3,2),(2,3)}και το τετράγωνο {(1,1), (1,2), (1,3), (2,3), (3,3), (3,2), (3,1), (2,1), (1,1)} δεν περνάνε από το κέντρο.
Για τη γενική περίπτωση:
Χωρίζω τα σχήματα στα εξής σύνολα:
- Ορθογώνια τρίγωνα = Α
- Ισοσκελή μη ορθογώνια τρίγωνα = Β
- Λοξά τετράγωνα (με κλίση -1, 1 στις πλευρές αντί για 0, άπειρο) = Γ
- Τετράγωνα = Δ
- Ορθογώνια = Ε
- Λοξά ορθογώνια (με κλίση -1, 1 στις πλευρές αντί για 0, άπειρο) = Ζ
- Τα σχήματα του συνόλου Β προκύπτουν από συνδυασμούς σχημάτων του Α με κοινή πλευρά
- Τα σχήματα του συνόλου Γ προκύπτουν από συνδυασμούς σχημάτων του Β με κοινή πλευρά
- Τα σχήματα του συνόλου Ζ προκύπτουν από συνδυασμούς σχημάτων του Γ με κοινή πλευρά ή "συνεχείς" συνδυασμούς σχημάτων του Ζ.
- Προσθέτοντας μια γραμμή σε ένα ορθογώνιο τρίγωνο, τα ορθογώνια τρίγωνα αυξάνονται κατά 5(n-2). Δηλαδή, γνωρίζοντας το μήκος της πλευράς ενός ορθ. τριγώνου, υπάρχει ο αναδρομικός τύπος b(n) = b(n-1) + 5(n-2).
- Τα σχήματα του συνόλου Γ είναι 1, 12, 26, ... για n = 3, n = 5, n = 7, ...

ΥΓ. Στο προηγούμενο μάλλον έπρεπε να βάλω δέσμευση στο 3π/2 και όχι στο 2π.
bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών και Πτυχιούχος του τμήματος Οικονομικής Επιστήμης ΟΠΑ. Έχει γράψει 343 μηνύματα.

25-09-22

23:08
Να αποδειχθεί ότι αν η από κοινού σ.π.π. fxy(x,y) είναι της μορφής fxy(x,y)=g(x)h(y) τότε οι X, Y είναι ανεξάρτητες τ.μ. και αντίστροφα. (Δεν ξέρω τι τρέχει με το λατεκ)
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

25-09-22

23:42
Αν έχουμε το ενδεχόμενο Β για τη μεταβλητή Χ και το ενδεχόμενο Γ για τη μεταβλητή Υ και Α = B τομή Γ, προκειμένου να είναι ανεξάρτητες οι Χ,Υ θα πρέπει P(A) = P(B)P(Γ), όποτε αυτά τα σύμβολα έχουν νόημα.
Νομίζω με λίγη algebruh/Θ. Fubini βγαίνει ότι το διπλό ολοκλήρωμα είναι πάντα το γινόμενο των 2 απλών.
Νομίζω με λίγη algebruh/Θ. Fubini βγαίνει ότι το διπλό ολοκλήρωμα είναι πάντα το γινόμενο των 2 απλών.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 4 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 67 μέλη διάβασαν αυτό το θέμα:
- mitskification
- Joji
- Panagiotis849
- GeorgePap2003
- Sherlockina
- eukleidhs1821
- Mariahj
- the purge
- kost28
- ggl
- χημεια4λαιφ
- katia.m
- KingOfPop
- sophiaa
- mpapa
- george777
- Maynard
- augustine
- tsiobieman
- igeorgeoikonomo
- notis_19
- globglogabgalab
- Unboxholics
- constansn
- Ymitheos
- DeWiN
- Georgekk
- aggelosst9
- Μάρκος Βασίλης
- spring day
- το κοριτσι του μαη
- papa2g
- SlimShady
- Nik13
- Lia 2006
- nucomer
- Johnman97
- Σωτηρία
- Εριφύλη
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

