Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

17-09-21

00:52
Το είπα είναι πουστια του σχολικου αλλά οκ αν είναι καθαρά εκτός ύλης οι συναρτήσεις ορισμένες σε μονοσύνολο τότε πάω πασο έχετε δίκιο
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

17-09-21

00:56
δεν εχει νοημα η αναζητηση του συγκεκριμενου οριου αφου η συναρτηση δεν οριζεται σε μια περιοχη του 1Το είπα είναι πουστια του σχολικου αλλά οκ αν είναι καθαρά εκτός ύλης οι συναρτήσεις ορισμένες σε μονοσύνολο τότε πάω πασο έχετε δίκιο
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

17-09-21

01:02
Το είπα είναι πουστια του σχολικου αλλά οκ αν είναι καθαρά εκτός ύλης οι συναρτήσεις ορισμένες σε μονοσύνολο τότε πάω πασο έχετε δίκιο
Δεν πειράζει, καλά έκανες και το ανέφερες γιατί σε ένα ευρύτερο πλαίσιο αυτά έχει σημασία να τα σκέφτεται κανείς. Στο πλαίσιο των απαιτήσεων του λυκείου όμως, ασκήσεις με τέτοιες συναρτήσεις δεν μπορούν να υπάρξουν. Τόσο γιατί δεν προσφέρουν ποικιλία αλλά και επειδή ο λογισμός δεν εφαρμόζεται, ο οποίος είναι και το κεντρικό θέμα των μαθηματικών Γ λυκείου. Ο ισχυρισμός λοιπόν ισχύει ύπο την προϋπόθεση αυτή που γράφεται με μικρά γράμματα περί τι είναι στην ύλη. Ειδάλλως έχεις δίκιο. Δεν ισχύει για δυο οποιεσδήποτε συναρτήσεις όποιες και εαν είναι αυτές. Μπράβο που το παρατήρησες όπως και να έχει. Στα λεπτά σημεία χαλάνε όλοι οι ορισμοί και για αυτό χρειάζεται προσοχή στο χτίσιμο και την διατύπωση τους συνήθως.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

17-09-21

11:39
μιας και στεκεστε στα λαθη του σχολικου ξεχασατε να πειτε για την κυρτοτητα που οριζεται βλακωδως στη γ λυκειου.
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

17-09-21

13:21
η κυρτοτητα οριζεται οπως οριζεται λογω της δομης της αναλυσης που εχει το βιβλιο.. επισης δεν θεωρω οτι υπαρχει καποιο λαθος γενικοτερα.. θα ερθει ο απειροστικος λογισμος στο πανεπιστημιο και καποια πραγματα θα διατυπωθουν αυστηροτεραμιας και στεκεστε στα λαθη του σχολικου ξεχασατε να πειτε για την κυρτοτητα που οριζεται βλακωδως στη γ λυκειου.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

17-09-21

13:44
εχεις δικιο σε αυτο.απλα τα παιδια εχουν μαθει την εννοια της εφαπτομενης θεωρω οτι επρεπε να οριζοταν με την εφαπτομενη ή με το ευθυγραμμο τμημα γενικοτερα και μετα να το πηγαινανε για διαφορισιμες συναρτησεις.η κυρτοτητα οριζεται οπως οριζεται λογω της δομης της αναλυσης που εχει το βιβλιο.. επισης δεν θεωρω οτι υπαρχει καποιο λαθος γενικοτερα.. θα ερθει ο απειροστικος λογισμος στο πανεπιστημιο και καποια πραγματα θα διατυπωθουν αυστηροτερα
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

19-09-21

02:34
|χ|+|y| ≥ |χ+y|
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

19-09-21

05:22
Έστω οτι δεν ισχύει αυτό. Έστω δηλαδή οτι :
|f'(α) + f'(b)| > k|b-α|
Επειδή όμως όπως πολύ σωστά μας είπε ο Αλέξανδρος, λόγω τριγωνικής ανισότητας
|x| + |y| > |x + y| , θα ισχύει :
|f'(α)| + |f'(b)| > k|b - α| (1)
Καθώς όμως f'(c) = 0, μπορούμε να προσθαφαιρέσουμε όπου θέλουμε αυτή την ποσότητα . Επίσης επειδή c E (α,b) εννοείται οτι b > α => b - α > 0 , c > α => c - α > 0 , b > c = > b - c > 0 επομένως : |b - α| = b - α , |c - α| = c - α και |b - c| = b - c . Βάσει των προηγούμενων η σχέση (1) γίνεται :
| [f'(c) - f'(α)]/(c - α) |(c - α) + | [f'(b) - f'(c)] / (b - c) |(b-c) > k(b-α) =>
Απο το ΘΜΤ όμως για την f' στα διαστήματα [α,c] και [c,b] μπορούμε να βρούμε ξ1 Ε (α,c) και ξ2 Ε (c,b) τέτοια ώστε :
f''(ξ1) = [f'(c) - f'(α)]/(c - α)
f''(ξ2) = [f'(b) - f'(c)] /(b - c)
|f''(ξ1)|(c - α) + |f''(ξ2)|(b - c) > k(b - α) (2)
Όμως :
|f''(ξ1)|(c-α) <= k(c-α)
|f''(ξ2)|(b-c) <= k(b-c)
Δηλαδή προσθέτοντας κατά μέλη τις δύο προηγούμενες :
|f''(ξ1)|(c-α) + |f''(ξ2)|(b-c) <= k(c-α) +k(b-c) (3)
Έτσι λοιπόν λόγω της μεταβατικής ιδιότητας της ανίσωσης συμπεραίνουμε :
k(c-α) +k(b-c) > k(b-α) =>
kc - kα + kb - kc > kb - kα =>
0 > 0
Το οποίο φυσικά είναι άτοπο.
Άρα πράγματι : |f'(α) + f'(β)| <= k|b - α|
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

19-09-21

15:55
Mια αλλη λυση:Έστω οτι δεν ισχύει αυτό. Έστω δηλαδή οτι :
|f'(α) + f'(b)| > k|b-α|
Επειδή όμως όπως πολύ σωστά μας είπε ο Αλέξανδρος, λόγω τριγωνικής ανισότητας
|x| + |y| > |x + y| , θα ισχύει :
|f'(α)| + |f'(b)| > k|b - α| (1)
Καθώς όμως f'(c) = 0, μπορούμε να προσθαφαιρέσουμε όπου θέλουμε αυτή την ποσότητα . Επίσης επειδή c E (α,b) εννοείται οτι b > α => b - α > 0 , c > α => c - α > 0 , b > c = > b - c > 0 επομένως : |b - α| = b - α , |c - α| = c - α και |b - c| = b - c . Βάσει των προηγούμενων η σχέση (1) γίνεται :
| [f'(c) - f'(α)]/(c - α) |(c - α) + | [f'(b) - f'(c)] / (b - c) |(b-c) > k(b-α) =>
Απο το ΘΜΤ όμως για την f' στα διαστήματα [α,c] και [c,b] μπορούμε να βρούμε ξ1 Ε (α,c) και ξ2 Ε (c,b) τέτοια ώστε :
f''(ξ1) = [f'(c) - f'(α)]/(c - α)
f''(ξ2) = [f'(b) - f'(c)] /(b - c)
|f''(ξ1)|(c - α) + |f''(ξ2)|(b - c) > k(b - α) (2)
Όμως :
|f''(ξ1)|(c-α) <= k(c-α)
|f''(ξ2)|(b-c) <= k(b-c)
Δηλαδή προσθέτοντας κατά μέλη τις δύο προηγούμενες :
|f''(ξ1)|(c-α) + |f''(ξ2)|(b-c) <= k(c-α) +k(b-c) (3)
Έτσι λοιπόν λόγω της μεταβατικής ιδιότητας της ανίσωσης συμπεραίνουμε :
k(c-α) +k(b-c) > k(b-α) =>
kc - kα + kb - kc > kb - kα =>
0 > 0
Το οποίο φυσικά είναι άτοπο.
Άρα πράγματι : |f'(α) + f'(β)| <= k|b - α|
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

19-09-21

16:55
Ωραίος,ευθεία απόδειξη !Mια αλλη λυση:
 + f'(b)|\leq |f'(a)| + |f'(b)| = |f'(c)-f'(a)|+|f'(b)-f'(c)|=\\ |\frac{f'(c)-f'(a)}{c-a}\cdot(c-a)| + |\frac{f'(b)-f'(c)}{b-c}\cdot (b-c)| = |f''(\xi_1)\cdot (c-a)| + |f''(\xi_2)\cdot (b-c)|=|f''(\xi)|\cdot | c-a| + |f''(\xi_2)| \cdot |b-c| \leq k|c-a|+k|b-c|=k\cdot (c-a) + k\cdot (b-c)=kc-ak+kb-kc=kb-ka=k(b-a)=k|b-a|)
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

20-09-21

03:09
νδο δεν υπαρχει κυρτη συναρτηση με 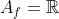 τετοια ωστε να ισχυει :
τετοια ωστε να ισχυει :+2f(1)=f'(1)+f(2)+f(0) )
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

20-09-21

04:19
νδο δεν υπαρχει κυρτη συναρτηση μετετοια ωστε να ισχυει :
+2f(1)=f'(1)+f(2)+f(0) )
Και αυτή με άτοπο θα την βγάλω, but it's okay,it's an honest method
 .
.Έστω οτι υπάρχει κυρτή συνάρτηση ορισμένη στο R που να ικανοποιεί την σχέση:
f'(0) + 2f(1) = f'(1) + f(2) + f(0) =>
f'(0) - f'(1) = f(2) + f(0) - 2f(1) =>
Εφόσον η f είναι κυρτή στο R, η f' είναι γνησίως αύξουσα στο R. Έτσι λοιπόν :
0 < 1 =>
f'(0) < f'(1) =>
f'(0) - f'(1) < 0
Σύμφωνα με την παραπάνω :
f(2) + f(0) - 2f(1) < 0 =>
[f(2) - f(1)]/[2 - 1] - [f(1) - f(0)]/[1 - 0] < 0 =>
Απο το ΘΜΤ για την f στο [0,1] και στο [1,2] βρίσκουμε ζ1 Ε (0,1) και ζ2 Ε (1,2) τέτοια ώστε η προηγούμενη να γίνει :
f'(ζ2) - f'(ζ1) < 0 =>
f'(ζ1) > f'(ζ2) , με ζ1 < ζ2 .
Το οποίο είναι άτοπο, αφού η f' είναι γνησίως αύξουσα στο R .
Άρα δεν μπορεί να υπάρχει συνάρτηση f, κυρτή και ορισμένη στο R με την παραπάνω ιδιότητα.
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

20-09-21

04:40
βλεπω δεν ειμαι μονο εγω που κοιμαμαι με τις κοτες αντι να ξυπναωΚαι αυτή με άτοπο θα την βγάλω, but it's okay,it's an honest method.
Έστω οτι υπάρχει κυρτή συνάρτηση ορισμένη στο R που να ικανοποιεί την σχέση:
f'(0) + 2f(1) = f'(1) + f(2) + f(0) =>
f'(0) - f'(1) = f(2) + f(0) - 2f(1) =>
Εφόσον η f είναι κυρτή στο R, η f' είναι γνησίως αύξουσα στο R. Έτσι λοιπόν :
0 < 1 =>
f'(0) < f'(1) =>
f'(0) - f'(1) < 0
Σύμφωνα με την παραπάνω :
f(2) + f(0) - 2f(1) < 0 =>
[f(2) - f(1)]/[2 - 1] - [f(1) - f(0)]/[1 - 0] < 0 =>
Απο το ΘΜΤ για την f στο [0,1] και στο [1,2] βρίσκουμε ζ1 Ε (0,1) και ζ2 Ε (1,2) τέτοια ώστε η προηγούμενη να γίνει :
f'(ζ2) - f'(ζ1) < 0 =>
f'(ζ1) > f'(ζ2) , με ζ1 < ζ2 .
Το οποίο είναι άτοπο, αφού η f' είναι γνησίως αύξουσα στο R .
Άρα δεν μπορεί να υπάρχει συνάρτηση f, κυρτή και ορισμένη στο R με την παραπάνω ιδιότητα.
 ..
..Αυτη τη φορα το ατοπο εχει τον πρωταγωνωνιστικο ρολο αν και αναμενομενο σε τετοια ασκηση
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

20-09-21

04:49
Άστα, τώρα που έβαλε πάλι ζέστες κιόλας η ημέρα είναι κόλαση για να κάνεις το οτιδήποτε σε σχέση με την νύχτα...βλεπω δεν ειμαι μονο εγω που κοιμαμαι με τις κοτες αντι να ξυπναω..
Αυτη τη φορα το ατοπο εχει τον πρωταγωνωνιστικο ρολο αν και αναμενομενο σε τετοια ασκηση
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

20-09-21

04:51
σωστοςΆστα, τώρα που έβαλε πάλι ζέστες κιόλας η ημέρα είναι κόλαση για να κάνεις το οτιδήποτε σε σχέση με την νύχτα...

νδο
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

20-09-21

23:33
Την προσπάθησα με διάφορους τρόπους αλλά δεν μου βγήκε.
Οπότε η έσχατη λύση... έθεσα : g(x) = (e^x - 1)ln(x+1) - x² .
Παραγωγίζουμε και καταλήγουμε σε ένα κλάσμα με παρανομαστή το χ+1 που είναι θετικό, και αριθμητή :
h(x) = (x+1)(e^x)ln(x+1) +e^x - 2x² - 2x - 1.
Παραγωγίζουμε 3 φορές και καταλήγουμε σε μια θετική ποσότητα, οπότε η h'''(x) > 0.
Άρα η h''(x) είναι γνησίως αύξουσα. Επειδή το χ = 0 είναι ρίζα της h''(x) έχουμε :
x > 0 => h''(x) > 0
x < 0 => h''(x) < 0
Άρα η h' είναι γνησίως αύξουσα για x > 0 και γνησίως φθίνουσα για x < 0 . Οπότε επειδή το 0 είναι ρίζα της h' έχουμε:
x > 0 => h'(x) > 0
x < 0 => h'(x) > 0
Οπότε η h(x) είναι γνησίως αύξουσα. Οπότε επειδή το 0 είναι ρίζα της h έχουμε :
x > 0 => h(x) > 0
x < 0 => h(x) < 0
Τελικά επειδή η g θα είναι γνησίως αύξουσα για x > 0 και γνησίως φθίνουσα για x < 0. Και επειδή το 0 είναι ρίζα και της g θα έχουμε:
x >= 0 = > g(x) >= 0
x < 0 => g(x) > 0
Σε κάθε περίπτωση : g(x) >= 0 ή ισοδύναμα : (e^x - 1)ln(x+1) >= x² για κάθε x E (-1,+oo).
Σημείωση όπου γράφω χ<0 εννοείται και x > -1 , αλλά για να μην χαθούμε στις λεπτομέρειες το παρέλειψα.
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

21-09-21

02:10
να δωσω hint , για μια λυση που εχω στο μυαλο μου?Την προσπάθησα με διάφορους τρόπους αλλά δεν μου βγήκε.
Οπότε η έσχατη λύση... έθεσα : g(x) = (e^x - 1)ln(x+1) - x² .
Παραγωγίζουμε και καταλήγουμε σε ένα κλάσμα με παρανομαστή το χ+1 που είναι θετικό, και αριθμητή :
h(x) = (x+1)(e^x)ln(x+1) +e^x - 2x² - 2x - 1.
Παραγωγίζουμε 3 φορές και καταλήγουμε σε μια θετική ποσότητα, οπότε η h'''(x) > 0.
Άρα η h''(x) είναι γνησίως αύξουσα. Επειδή το χ = 0 είναι ρίζα της h''(x) έχουμε :
x > 0 => h''(x) > 0
x < 0 => h''(x) < 0
Άρα η h' είναι γνησίως αύξουσα για x > 0 και γνησίως φθίνουσα για x < 0 . Οπότε επειδή το 0 είναι ρίζα της h' έχουμε:
x > 0 => h'(x) > 0
x < 0 => h'(x) > 0
Οπότε η h(x) είναι γνησίως αύξουσα. Οπότε επειδή το 0 είναι ρίζα της h έχουμε :
x > 0 => h(x) > 0
x < 0 => h(x) < 0
Τελικά επειδή η g θα είναι γνησίως αύξουσα για x > 0 και γνησίως φθίνουσα για x < 0. Και επειδή το 0 είναι ρίζα και της g θα έχουμε:
x >= 0 = > g(x) >= 0
x < 0 => g(x) > 0
Σε κάθε περίπτωση : g(x) >= 0 ή ισοδύναμα : (e^x - 1)ln(x+1) >= x² για κάθε x E (-1,+oo).
Σημείωση όπου γράφω χ<0 εννοείται και x > -1 , αλλά για να μην χαθούμε στις λεπτομέρειες το παρέλειψα.
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

21-09-21

02:12
η συναρτηση στο δ θεμα καλη φαινεται: https://drive.google.com/file/d/0Bx...UEE/edit?resourcekey=0-ubRmEetyhx8Xd5bUTOlEXg
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 6 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

