Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

16-09-21

07:23
Καλημέρα.
Το β αποδεικνύεται παίρνοντας την παράγωγο της συναρτησιακής σχέσης απο όπου προκύπτει f'(x) > 0 άρα f γνησίως αύξουσα. Η κυρτότητα βγαίνει παίρνοντας την δεύτερη παράγωγο. Προκύπτει ένα κλάσμα λόγω της πρώτης παραγώγου, του οποίου ο αριθμητής μέσω πράξεων βγαίνει πάντα θετικός. Ο παρανομαστής επίσης.
Όσον αφορά στο γ :
f(x) > sqrt(e^x)
f(x)lnf(x) > sqrt(e^x)lnf(x)
e^(-x/2) > lnf(x)
e^(e^(-x/2)) > f(x)
Τελικά :
sqrt(e^x) < f(x) < e^(e^(-x/2)) => x > 0 στο +οο
sqrt(e^x)/χ < f(x)/χ < e^(e^(-x/2))χ
Απο το κριτήριο παρεμβολής επειδή τόσο το όριο του άνω και κάτω φράγματος πάνε στο +οο όταν το χ πλησιάζει το +οο, και η ποσότητα f(x)/x θα πλησιάζει το +οο .
Επιπλέον για το ζητούμενο όριο έχουμε :
1 < 1+lnx/f(x) < 1+x/f(x) =>
1 < 1+lnx/f(x) < 1+1/f(x)/x =>
1 < [1+lnx/f(x)]^(f(x)/x) < [1 + 1/f(x)/x]^(f(x)/x)
Εν τέλει πάλι απο το κριτήριο παρεμβολής βρίσκουμε οτι τόσο το κάτω όσο και το άνω φράγμα έχει όριο το 1 στο +οο . Άρα το όριο της φραγμενης ποσότητας μας δίνει 1.
Για το δ :
Παρατηρούμε καταρχάς οτι το 2 είναι ρίζα της εξίσωσης.
Έπειτα θέτουμε : g(x) = 2[f(x) - f(2)] + x[f(2) - f(4)] - 2[f(2) - f(4)]
g'(x) = 2f'(x) + f(2) - f(4) .
Θέτουμε g'(x) = 0 =>
2f'(x) + f(2) - f(4) = 0 =>
f'(x) = f(4) - f(2) / 2 = [f(4) - f(2)] / (4 - 2)
Πράγματι απο το ΘΜΤ για την f στο [2,4] υπάρχει ξ που να ικανοποιεί τέτοια συνθήκη και επίσης είναι μοναδικό καθώς η f είναι κυρτή και επομένως η f' γνησίως αύξουσα. Άρα για x < ξ => g'(ξ) < 0 ενώ για x > ξ => g'(ξ) > 0 .
Παρατήρηση λοιπόν : εαν δείξω οτι ξ = 2 τελείωσα.
g(ξ) = 2[f(ξ) - f(2)] + ξ[f(2) - f(4)] - 2[f(2) - f(4)]
Η εφαπτομένη της f στο ξ είναι :
y - f(ξ) = f'(ξ)(χ-ξ) =>
y - f(ξ) = [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2
y = [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2 + f(ξ) => f κυρτή
f(x) >= [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2 + f(ξ) => με την ισότητα να ισχύει μόνο αν x = ξ
2[f(x) - f(ξ)] >= -x[f(2) - f(4)] + ξ[f(2) - f(4)]
2[f(x) - f(ξ)] + x[f(2) - f(4)] - ξ[f(2) - f(4)] >= 0
2[f(ξ) - f(x)] - x[f(2) - f(4)] + ξ[f(2) - f(4)] <= 0
Για x = 2 στην παραπάνω :
g(ξ) <= 0 , με την ισότητα να μπορει να ισχύει μόνο όταν ξ = 2 .
Τελικά επειδή g(ξ) = g(2) = 0 , και επειδή αυτό το σημείο είναι ελάχιστο της g, συμπεραίνουμε ότι το x = 2 είναι μοναδική λύση της αρχικής εξίσωσης.
Το β αποδεικνύεται παίρνοντας την παράγωγο της συναρτησιακής σχέσης απο όπου προκύπτει f'(x) > 0 άρα f γνησίως αύξουσα. Η κυρτότητα βγαίνει παίρνοντας την δεύτερη παράγωγο. Προκύπτει ένα κλάσμα λόγω της πρώτης παραγώγου, του οποίου ο αριθμητής μέσω πράξεων βγαίνει πάντα θετικός. Ο παρανομαστής επίσης.
Όσον αφορά στο γ :
f(x) > sqrt(e^x)
f(x)lnf(x) > sqrt(e^x)lnf(x)
e^(-x/2) > lnf(x)
e^(e^(-x/2)) > f(x)
Τελικά :
sqrt(e^x) < f(x) < e^(e^(-x/2)) => x > 0 στο +οο
sqrt(e^x)/χ < f(x)/χ < e^(e^(-x/2))χ
Απο το κριτήριο παρεμβολής επειδή τόσο το όριο του άνω και κάτω φράγματος πάνε στο +οο όταν το χ πλησιάζει το +οο, και η ποσότητα f(x)/x θα πλησιάζει το +οο .
Επιπλέον για το ζητούμενο όριο έχουμε :
1 < 1+lnx/f(x) < 1+x/f(x) =>
1 < 1+lnx/f(x) < 1+1/f(x)/x =>
1 < [1+lnx/f(x)]^(f(x)/x) < [1 + 1/f(x)/x]^(f(x)/x)
Εν τέλει πάλι απο το κριτήριο παρεμβολής βρίσκουμε οτι τόσο το κάτω όσο και το άνω φράγμα έχει όριο το 1 στο +οο . Άρα το όριο της φραγμενης ποσότητας μας δίνει 1.
Για το δ :
Παρατηρούμε καταρχάς οτι το 2 είναι ρίζα της εξίσωσης.
Έπειτα θέτουμε : g(x) = 2[f(x) - f(2)] + x[f(2) - f(4)] - 2[f(2) - f(4)]
g'(x) = 2f'(x) + f(2) - f(4) .
Θέτουμε g'(x) = 0 =>
2f'(x) + f(2) - f(4) = 0 =>
f'(x) = f(4) - f(2) / 2 = [f(4) - f(2)] / (4 - 2)
Πράγματι απο το ΘΜΤ για την f στο [2,4] υπάρχει ξ που να ικανοποιεί τέτοια συνθήκη και επίσης είναι μοναδικό καθώς η f είναι κυρτή και επομένως η f' γνησίως αύξουσα. Άρα για x < ξ => g'(ξ) < 0 ενώ για x > ξ => g'(ξ) > 0 .
Παρατήρηση λοιπόν : εαν δείξω οτι ξ = 2 τελείωσα.
g(ξ) = 2[f(ξ) - f(2)] + ξ[f(2) - f(4)] - 2[f(2) - f(4)]
Η εφαπτομένη της f στο ξ είναι :
y - f(ξ) = f'(ξ)(χ-ξ) =>
y - f(ξ) = [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2
y = [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2 + f(ξ) => f κυρτή
f(x) >= [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2 + f(ξ) => με την ισότητα να ισχύει μόνο αν x = ξ
2[f(x) - f(ξ)] >= -x[f(2) - f(4)] + ξ[f(2) - f(4)]
2[f(x) - f(ξ)] + x[f(2) - f(4)] - ξ[f(2) - f(4)] >= 0
2[f(ξ) - f(x)] - x[f(2) - f(4)] + ξ[f(2) - f(4)] <= 0
Για x = 2 στην παραπάνω :
g(ξ) <= 0 , με την ισότητα να μπορει να ισχύει μόνο όταν ξ = 2 .
Τελικά επειδή g(ξ) = g(2) = 0 , και επειδή αυτό το σημείο είναι ελάχιστο της g, συμπεραίνουμε ότι το x = 2 είναι μοναδική λύση της αρχικής εξίσωσης.
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

16-09-21

10:15
Το όριο του άνω φράγματος δεν είναι e; Αν θέσουμε f(x)/x=u καταλήγουμε στον ορισμό του e
Επίσης στο δ είναι ριζα και η x=4
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Επίσης στο δ είναι ριζα και η x=4
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

16-09-21

12:14
Αυτη η υψωση σε μεταβλητη δυναμη δεν ξερω κατα ποσο νομιμη ειναι θελει συζητηση, τελος παντων το οριο αντιμετομιζεται πιο στοιχειωδως (υψωσι εις την e^{..} και μετα συνεχιζεις) .Επισης στο τελευταιο σαν λυση ειναι και το 4, θα φτιαξω καφε και θα δω πιο καθαρα την συγκεκριμενη προσπαθεια.Καλημέρα.
Το β αποδεικνύεται παίρνοντας την παράγωγο της συναρτησιακής σχέσης απο όπου προκύπτει f'(x) > 0 άρα f γνησίως αύξουσα. Η κυρτότητα βγαίνει παίρνοντας την δεύτερη παράγωγο. Προκύπτει ένα κλάσμα λόγω της πρώτης παραγώγου, του οποίου ο αριθμητής μέσω πράξεων βγαίνει πάντα θετικός. Ο παρανομαστής επίσης.
Όσον αφορά στο γ :
f(x) > sqrt(e^x)
f(x)lnf(x) > sqrt(e^x)lnf(x)
e^(-x/2) > lnf(x)
e^(e^(-x/2)) > f(x)
Τελικά :
sqrt(e^x) < f(x) < e^(e^(-x/2)) => x > 0 στο +οο
sqrt(e^x)/χ < f(x)/χ < e^(e^(-x/2))χ
Απο το κριτήριο παρεμβολής επειδή τόσο το όριο του άνω και κάτω φράγματος πάνε στο +οο όταν το χ πλησιάζει το +οο, και η ποσότητα f(x)/x θα πλησιάζει το +οο .
Επιπλέον για το ζητούμενο όριο έχουμε :
1 < 1+lnx/f(x) < 1+x/f(x) =>
1 < 1+lnx/f(x) < 1+1/f(x)/x =>
1 < [1+lnx/f(x)]^(f(x)/x) < [1 + 1/f(x)/x]^(f(x)/x)
Εν τέλει πάλι απο το κριτήριο παρεμβολής βρίσκουμε οτι τόσο το κάτω όσο και το άνω φράγμα έχει όριο το 1 στο +οο . Άρα το όριο της φραγμενης ποσότητας μας δίνει 1.
Για το δ :
Παρατηρούμε καταρχάς οτι το 2 είναι ρίζα της εξίσωσης.
Έπειτα θέτουμε : g(x) = 2[f(x) - f(2)] + x[f(2) - f(4)] - 2[f(2) - f(4)]
g'(x) = 2f'(x) + f(2) - f(4) .
Θέτουμε g'(x) = 0 =>
2f'(x) + f(2) - f(4) = 0 =>
f'(x) = f(4) - f(2) / 2 = [f(4) - f(2)] / (4 - 2)
Πράγματι απο το ΘΜΤ για την f στο [2,4] υπάρχει ξ που να ικανοποιεί τέτοια συνθήκη και επίσης είναι μοναδικό καθώς η f είναι κυρτή και επομένως η f' γνησίως αύξουσα. Άρα για x < ξ => g'(ξ) < 0 ενώ για x > ξ => g'(ξ) > 0 .
Παρατήρηση λοιπόν : εαν δείξω οτι ξ = 2 τελείωσα.
g(ξ) = 2[f(ξ) - f(2)] + ξ[f(2) - f(4)] - 2[f(2) - f(4)]
Η εφαπτομένη της f στο ξ είναι :
y - f(ξ) = f'(ξ)(χ-ξ) =>
y - f(ξ) = [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2
y = [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2 + f(ξ) => f κυρτή
f(x) >= [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2 + f(ξ) => με την ισότητα να ισχύει μόνο αν x = ξ
2[f(x) - f(ξ)] >= -x[f(2) - f(4)] + ξ[f(2) - f(4)]
2[f(x) - f(ξ)] + x[f(2) - f(4)] - ξ[f(2) - f(4)] >= 0
2[f(ξ) - f(x)] - x[f(2) - f(4)] + ξ[f(2) - f(4)] <= 0
Για x = 2 στην παραπάνω :
g(ξ) <= 0 , με την ισότητα να μπορει να ισχύει μόνο όταν ξ = 2 .
Τελικά επειδή g(ξ) = g(2) = 0 , και επειδή αυτό το σημείο είναι ελάχιστο της g, συμπεραίνουμε ότι το x = 2 είναι μοναδική λύση της αρχικής εξίσωσης.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

16-09-21

13:07
Αυτη η υψωση σε μεταβλητη δυναμη δεν ξερω κατα ποσο νομιμη ειναι θελει συζητηση, τελος παντων το οριο αντιμετομιζεται πιο στοιχειωδως (υψωσι εις την e^{..} και μετα συνεχιζεις) .Επισης στο τελευταιο σαν λυση ειναι και το 4, θα φτιαξω καφε και θα δω πιο καθαρα την συγκεκριμενη προσπαθεια.
Ναι εκείνο το σημείο το σκεφτόμουν και εγώ λίγο αλλά πρέπει να γίνεται λογικά γιατί οι βάσεις είναι >= 1 κοντά στο +οο .
Για το δ έχεις δίκιο, θέλει λίγη διόρθωση. Θα το κοιτάξω και εγώ εάν είναι το απόγευμα πάλι.
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

16-09-21

13:17
Η ύψωση σε μεταβλητή δύναμη είναι νόμιμη, αλλά το όριο του άνω φράγματος δεν είναι 1 και δεν υπάρχει η ίσο σύγκλιση του κριτηρίου παρεμβολης
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

16-09-21

13:41
Η ύψωση σε μεταβλητή δύναμη είναι νόμιμη, αλλά το όριο του άνω φράγματος δεν είναι 1 και δεν υπάρχει η ίσο σύγκλιση του κριτηρίου παρεμβολης
Έχεις δίκιο. Ενταξει μικρό το κακό it's almost there εφόσον δεν είναι 0 η απειρο. Άρα πρέπει το άνω φράγμα να διαιρεθεί με e και ξεχωριστά να δειχτεί ότι και πάλι είναι άνω φράγμα.
Το κριτήριο παρεμβολής εφαρμόζεται διότι όταν ισχύει καθαρά η ανίσωση τότε ισχύει και η ανισόισοτητα αφού είναι ισότητα ή ανισότητα. Δεν είναι όπως στο σχολικό αλλά έτσι είναι.
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

16-09-21

13:56
αμα ηταν νομιμη παντα θα ισχυε :Η ύψωση σε μεταβλητή δύναμη είναι νόμιμη, αλλά το όριο του άνω φράγματος δεν είναι 1 και δεν υπάρχει η ίσο σύγκλιση του κριτηρίου παρεμβολης
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

16-09-21

13:59
ισχυει για μεγαλες τιμες του x αυτο
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

16-09-21

14:31
γενικα δεν ειναι νομιμη και δεν ισχυει παντα, γιατι ο εκθετης μπορει να μεταβαλεται διαφορετικα σε σχεση με τον εκθετη, μπορω να βρω παραδειγματα που ισχυει αυτο. Το πιο ευκολο με τριγωνομετρικες συναρτησεις αλλα εδω περα ειναι κομπλε ωστοσο σε επιπεδο γ λυκειου θα υπαρξει θεμα αν γινει κατι τετοια σε μια εξεταση.ισχυει για μεγαλες τιμες του x αυτο
Το οριο παντως αντιμετωπιζεται πιο απλα, θα γραψω λυση αργοτερα τοσο και για το τελευταιο,μπορεις να γραψεις και εσυ αν θελεις την λυση σου
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

16-09-21

14:34
γενικα δεν ειναι νομιμη και δεν ισχυει παντα, γιατι ο εκθετης μπορει να μεταβαλεται διαφορετικα σε σχεση με τον εκθετη, μπορω να βρω παραδειγματα που ισχυει αυτο. Το πιο ευκολο με τριγωνομετρικες συναρτησεις αλλα εδω περα ειναι κομπλε ωστοσο σε επιπεδο γ λυκειου θα υπαρξει θεμα αν γινει κατι τετοια σε μια εξεταση.
Το οριο παντως αντιμετωπιζεται πιο απλα, θα γραψω λυση αργοτερα τοσο και για το τελευταιο,μπορεις να γραψεις και εσυ αν θελεις την λυση σου
Δεν νομίζω να υπάρξει πρόβλημα, το σχολικό χρησιμοποιεί εκφράσεις για το τι γίνεται "κοντά" στο χο. Οπότε κάποιος μπορεί να χτίσει σχετικά επιχειρήματα. Στο παράδειγμα που έθεσες λόγου χάρη το 2^x < 3^x ισχύει για μεγάλες τιμές του χ σαν αυτές που παίρνει όταν πάει στο άπειρο. Δεν ισχύει για κάθε x E R προφανώς αλλά αυτό δεν σημαίνει οτι αχρηστεύει την σημασία της σχέσης να χρησιμοποιηθεί ως ανισότητα. Αυτό ύπο την έννοια οτι υπάρχει xo τέτοιο ώστε όταν x>xo να ισχύει η δοθείσα σχέση. Σε αυτή την περίπτωση θα μπορούσε λοιπόν κάποιος να πει οτι για x > 1 ισχύει το παραπάνω, οπότε για x->+oo να την χρησιμοποιήσει.
ΥΓ. Δεν ξέρω που έχω κάνει λάθος στο δ , αλλά φαντάζομαι κάπου εκεί που κάνω αναφορά στο οτι το ξ πρέπει να είναι επίσης 2.
Ο πιο ασφαλής τρόπος θα ήταν να γίνει Rolle στο [2,4] λοιπόν εφόσον g(2)=g(4) = 0 να δικαιολογηθεί πάλι οτι η g είναι γνησίως φθίνουσα πριν το ξ και γνησίως αύξουσα μετά το ξ και να δειχτεί κάπως οτι το g(ξ) < 0 . Θα το ψάξω περαιτέρω μόλις βρω τον χρόνο όμως γιατί δεν έχει νόημα να πετάξω την λύση χωρίς να δω πιο επιχείρημα την στράβωσε και το κυριότερο το γιατί.
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

16-09-21

15:13
νομιζω το κουραζεις λιγο αδικα.. ξερεις οτι η g ειναι γνησιως φθινουσα στοΚαλημέρα.
Το β αποδεικνύεται παίρνοντας την παράγωγο της συναρτησιακής σχέσης απο όπου προκύπτει f'(x) > 0 άρα f γνησίως αύξουσα. Η κυρτότητα βγαίνει παίρνοντας την δεύτερη παράγωγο. Προκύπτει ένα κλάσμα λόγω της πρώτης παραγώγου, του οποίου ο αριθμητής μέσω πράξεων βγαίνει πάντα θετικός. Ο παρανομαστής επίσης.
Όσον αφορά στο γ :
f(x) > sqrt(e^x)
f(x)lnf(x) > sqrt(e^x)lnf(x)
e^(-x/2) > lnf(x)
e^(e^(-x/2)) > f(x)
Τελικά :
sqrt(e^x) < f(x) < e^(e^(-x/2)) => x > 0 στο +οο
sqrt(e^x)/χ < f(x)/χ < e^(e^(-x/2))χ
Απο το κριτήριο παρεμβολής επειδή τόσο το όριο του άνω και κάτω φράγματος πάνε στο +οο όταν το χ πλησιάζει το +οο, και η ποσότητα f(x)/x θα πλησιάζει το +οο .
Επιπλέον για το ζητούμενο όριο έχουμε :
1 < 1+lnx/f(x) < 1+x/f(x) =>
1 < 1+lnx/f(x) < 1+1/f(x)/x =>
1 < [1+lnx/f(x)]^(f(x)/x) < [1 + 1/f(x)/x]^(f(x)/x)
Εν τέλει πάλι απο το κριτήριο παρεμβολής βρίσκουμε οτι τόσο το κάτω όσο και το άνω φράγμα έχει όριο το 1 στο +οο . Άρα το όριο της φραγμενης ποσότητας μας δίνει 1.
Για το δ :
Παρατηρούμε καταρχάς οτι το 2 είναι ρίζα της εξίσωσης.
Έπειτα θέτουμε : g(x) = 2[f(x) - f(2)] + x[f(2) - f(4)] - 2[f(2) - f(4)]
g'(x) = 2f'(x) + f(2) - f(4) .
Θέτουμε g'(x) = 0 =>
2f'(x) + f(2) - f(4) = 0 =>
f'(x) = f(4) - f(2) / 2 = [f(4) - f(2)] / (4 - 2)
Πράγματι απο το ΘΜΤ για την f στο [2,4] υπάρχει ξ που να ικανοποιεί τέτοια συνθήκη και επίσης είναι μοναδικό καθώς η f είναι κυρτή και επομένως η f' γνησίως αύξουσα. Άρα για x < ξ => g'(ξ) < 0 ενώ για x > ξ => g'(ξ) > 0 .
Παρατήρηση λοιπόν : εαν δείξω οτι ξ = 2 τελείωσα.
g(ξ) = 2[f(ξ) - f(2)] + ξ[f(2) - f(4)] - 2[f(2) - f(4)]
Η εφαπτομένη της f στο ξ είναι :
y - f(ξ) = f'(ξ)(χ-ξ) =>
y - f(ξ) = [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2
y = [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2 + f(ξ) => f κυρτή
f(x) >= [f(4) - f(2)]χ/2 - ξ[f(4) - f(2)]/2 + f(ξ) => με την ισότητα να ισχύει μόνο αν x = ξ
2[f(x) - f(ξ)] >= -x[f(2) - f(4)] + ξ[f(2) - f(4)]
2[f(x) - f(ξ)] + x[f(2) - f(4)] - ξ[f(2) - f(4)] >= 0
2[f(ξ) - f(x)] - x[f(2) - f(4)] + ξ[f(2) - f(4)] <= 0
Για x = 2 στην παραπάνω :
g(ξ) <= 0 , με την ισότητα να μπορει να ισχύει μόνο όταν ξ = 2 .
Τελικά επειδή g(ξ) = g(2) = 0 , και επειδή αυτό το σημείο είναι ελάχιστο της g, συμπεραίνουμε ότι το x = 2 είναι μοναδική λύση της αρχικής εξίσωσης.
H λυση σου θεωρω ειναι η πιο υποδειγματικη απο την αποψη οτι θα την ακολουθησει η πλειοψηφια
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

16-09-21

15:23
Yuup this makes more sense.νομιζω το κουραζεις λιγο αδικα.. ξερεις οτι η g ειναι γνησιως φθινουσα στοκαι γνησιως αυξουσα στο
με g(2)=0 αρα δεν μηδενιζεται πουθενα αλλου στο
, αρα θα δουμε αν μηδενιζεται πουθενα στο
η σκεψη μας ειναι να δουμε το προσημο του g(4) αν ειναι θετικο τοτε απο bolzano θα υπαρχει υπαρξιακη λυση στο
αν αντικαταστησουμε βλεπουμε οτι το g(4)=0 αρα δεν μηδενιζεται πουθενα αλλου η συναρτηση , εκτος απο τις θεσεις χ=2,χ=4.
H λυση σου θεωρω ειναι η πιο υποδειγματικη απο την αποψη οτι θα την ακολουθησει η πλειοψηφια
Κοιτώντας μια φορά πάλι την λύση ούτως η άλλως απο το ΘΜΤ το ξ Ε (2,4), οπότε εξορισμού δεν θα μπορούσε ποτέ να ήταν ξ = 2 όπως ισχυρίζομαι στο τέλος. Είναι άτοπο και για αυτό αποτυγχάνει η λύση να πιάσει την άλλη ρίζα και εκεί αποτυγχάνει κυρίως το πράγμα...Πρέπει να σταματήσω να τα απαντάω αυτά αργά μου φαίνεται
 .
.asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

16-09-21

16:14
τελικα σωστη ηταν αλλα ο καφες δεν εχει επιδρασει ακομα δυστηχως.Επειδη βαριεμαι να το ξαναγραφω σε latex ,κανουμε το συγκεκριμενο οριο στην μορφη e^{..} και παρακατω υπολογιζουμε το οριο του εκθετη
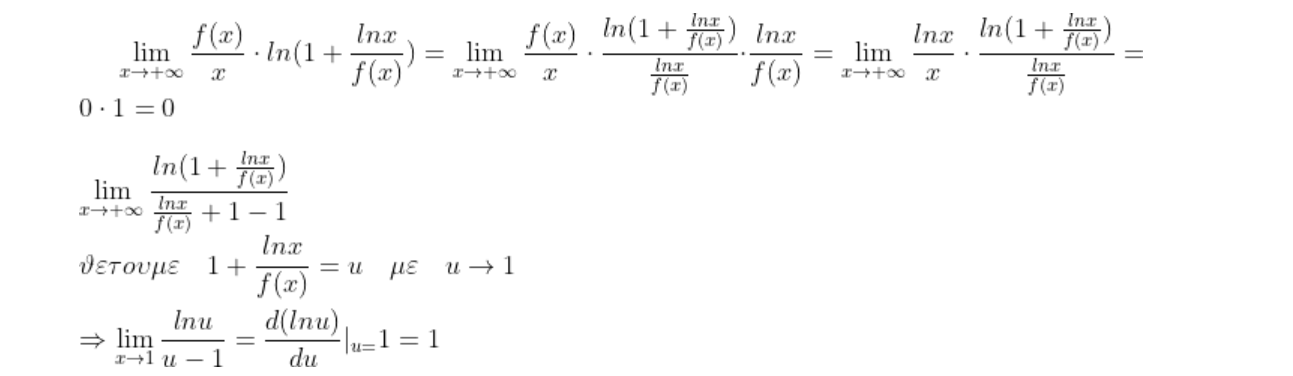
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

16-09-21

17:28
Ουσιαστικά ελένισες. Έτσι το είχα κάνει και εγώ αρχικά αλλά κατέληγε σε απροσδιοριστία και βαριόμουν να το φτιάξω οπότε προσπάθησα να το φράξω
View attachment 85693
για καποιο λογο το latex εδω τα επαιξε με μια συγκεκριμενη εκφραση και αναγκαζομαι να γραψω σε ξεχωριστο editor
 .
.Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

16-09-21

21:04
μια απλη αλλα καλη
αν lim (f^2(x)+g^2(χ)),x->xo = 0 να βρειτε το οριο της f και το οριο της g στο χο
και ενας ισχυρισμος
αν limf(x),x-χο = λεIR και limg(x),x>xo = κεIR τοτε
lim (f(x)+g(x)), x->xo = κ+λ
αν lim (f^2(x)+g^2(χ)),x->xo = 0 να βρειτε το οριο της f και το οριο της g στο χο
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
και ενας ισχυρισμος
αν limf(x),x-χο = λεIR και limg(x),x>xo = κεIR τοτε
lim (f(x)+g(x)), x->xo = κ+λ
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

16-09-21

21:49
για το 1ο :μια απλη αλλα καλη
αν lim (f^2(x)+g^2(χ)),x->xo = 0 να βρειτε το οριο της f και το οριο της g στο χο
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
και ενας ισχυρισμος
αν limf(x),x-χο = λεIR και limg(x),x>xo = κεIR τοτε
lim (f(x)+g(x)), x->xo = κ+λ
ομοια προκυπτει :
γνωριζουμε οτι:
ομοια για την f
o ισχυρισμος ειναι σωστος, μηπως ηθελες να γραψεις κατι αλλο
 ?
?Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

17-09-21

00:21
Μια ίσως πιο τσιμπημένη αλλά όχι πολύ μακριά απο το λύκειο : Να βρεθεί μια συνάρτηση f που να ικανοποιεί την σχέση :
f'(x) = f-1(x)
f'(x) = f-1(x)
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

17-09-21

00:29
Ο ισχυρισμός σύμφωνα με το σχολικό είναι αληθης αλλά αν f(x)=ριζα(χ-1) και g(x)=ριζα(1-χ),χο=1, το όριο του αθροίσματος δεν οριζεται
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

17-09-21

00:34
Ναι γιατί δεν έχει νόημα να μιλήσεις για το όριο μιας τέτοιας ποσότητας αφού έχει πεδίο ορισμού το :Ο ισχυρισμός σύμφωνα με το σχολικό είναι αληθης αλλά αν f(x)=ριζα(χ-1) και g(x)=ριζα(1-χ),χο=1, το όριο του αθροίσματος δεν οριζεται
Df+g = {1}
Τέτοιες συναρτήσεις όμως απο όσο θυμάμαι δεν μελετώνται στα πλαίσια της Γ λυκείου και η ύπαρξη τους αγνοείται.
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

17-09-21

00:44
Ο ισχυρισμός σύμφωνα με το σχολικό είναι αληθης αλλά αν f(x)=ριζα(χ-1) και g(x)=ριζα(1-χ),χο=1, το όριο του αθροίσματος δεν οριζεται
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 11 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

