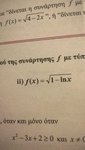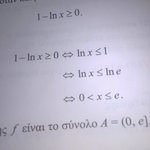Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[Samael]

f1(x) =e^x
f2(x) =x^2
f3(x)=ημχ

Να γραφούν ως σύνθεση των παραπάνω:
ημ²e^x
ημe^2x
ε^ημχ⁴
ημ⁴*e^2x

Μπορεί κάποιος να μου εξηγήσει πως σκεφτόμαστε εδώ;

Προσπαθείς απο έξω προς τα μέσα να αναγνωρίσεις ποιά συνάρτηση έχει μπέσα στην άλλη . Λόγου χάρη :

ημ²(e^x) = (ημ(e^x))²

Αρα η συνάρτηση αυτή μπορεί να γραφτεί ως :

f2(g(x)) οπου g(x) = ημ(e^x) .

Παρατηρείς οτι η g(x) μπορεί να γραφτεί ως g(x) = f3(h(x))

Όμως έτσι μένει οτι h(x) = e^x = f1(x)

Αρα τελικά η συνάρτηση γράφεται ως :

f2(f3(f1(x)))

Δες το ανάποδα τώρα :

f2(x) = x²

και f3(x) = ημx

Αρα f2(f3(x)) = (ημx)² = ημ²x

f1(x) = e^x

Αρα f2(f3(f1(x))) = ημ²(e^x)

Ουσιαστικά βάζεις όπου θα έπρεπε να ήταν στην αρχική το x τον τύπο της νεας συνάρτησης .

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[asdfqwerty]

f1(x) =e^x
f2(x) =x^2
f3(x)=ημχ

Να γραφούν ως σύνθεση των παραπάνω:
ημ²e^x
ημe^2x
ε^ημχ⁴
ημ⁴*e^2x

Μπορεί κάποιος να μου εξηγήσει πως σκεφτόμαστε εδώ;

Κοιτάς ποια συνάρτηση δέχεται πρώτη το Χ και ποια δέχεται την κάθε προηγούμενη τιμή
Πχ για το πρώτο παράδειγμα
f(x)= [cos(e^x)]^2
Σκέψου ότι θέλουμε το f(1)
To 1 θα το δεχτεί πρώτα η e^x θα βγάλει για τιμή το e ,μετά την τιμή της εκθετικής θα την πάρει η ημίτονο και θα υπολογίσει την τιμή ημe , και τέλος η τιμή που θα βγάλει το ημίτονο θα τετραγωνίστει απο την τελευταία συνάρτηση όπου είναι η x^2 και θα βγάλει το (ημe)^2=f(1)
Την σύνθεση την ορίζεις βαση ποια παίρνει πρώτα το Χ και ποια τελευταία
f2(f3(f1(x))))

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Jack25]

f1(x) =e^x
f2(x) =x^2
f3(x)=ημχ

Να γραφούν ως σύνθεση των παραπάνω:
i)ημ²e^x
ii)ημe^2x
iii)ε^ημχ⁴
iv)ημ⁴*e^2x

Μπορεί κάποιος να μου εξηγήσει πως σκεφτόμαστε εδώ;

κάθε συνάρτηση είναι ένας κανόνας που αντιστοιχίζει την είσοδο σε κάποια έξοδο ,
η είσοδος συνηθίζεται να είναι μια απλή μεταβλητή x
το παραπάνω ερώτημα ανάγεται στο με ποια σειρά πρέπει να εφαρμόσουμε τους 3 κανόνες , δηλαδή τις f1,f2 και f3 για να προκύψει ο τελικός κανόνας που είναι η τελική συνάρτηση , η σύνθεση
στο i)
1. εφαρμόζεις τον f1 και έτσι
από x παίρνεις e^x = f1(x)

2. εφαρμόζεις τον f3 στην έξοδο του 1ου κατα σειρά εφαρμογής κανόνα και
από e^x παίρνεις ημ(e^x ) = f3(f1(x))

3. εφαρμόζεις τον f2 στην έξοδο του 2ου κατά σειρά εφαρμογής κανόνα και
από ημ(e^x ) παίρνεις (ημ(e^x))^2 = f2(f3(f1(x)))

στο iii)
1. από x σε ημx = f3(x)

2. από ημx σε (ημx)^2= f2(f3(x))

3. από (ημx)^2 σε ((ημx)^2)^2 = (ημx)^4 = f2(f2(f3(x)))

4. από (ημx)^4 σε e^((ημx)^4) = f1(f2(f2(f3(x))))

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[aggelosst9]

f(x)=(x+1)/x , x>1
f(x)=x^2+1, x≤1
Να βρείτε τα σημεία της Cf στα οποία η εφαπτομένη είναι παράλληλη προς την ευθεία y=-(1/4)x+2018 και να γράψετε τις εξισώσεις των εφαπτομένων στα σημεία αυτά.

Πήρα f'(x)=-1/4 και βρήκα τις παραγώγους, αλλά δεν μου βγαίνει η f παραγωγίσιμη στο 1.
Λύνεται κάπως αλλιώς; Γιατί αν δείξω ότι είναι Παρ/μη μετά λογικά παίρνω f'(x)=-1/4 για τις δύο παραγώγους και βρίσκω 2-3 σημεία.
Καλή χρονιά!

 

[Samael]

f(x)=(x+1)/x , x>1
f(x)=x^2+1, x≤1
Να βρείτε τα σημεία της Cf στα οποία η εφαπτομένη είναι παράλληλη προς την ευθεία y=-(1/4)x+2018 και να γράψετε τις εξισώσεις των εφαπτομένων στα σημεία αυτά.

Πήρα f'(x)=-1/4 και βρήκα τις παραγώγους, αλλά δεν μου βγαίνει η f παραγωγίσιμη στο 1.
Λύνεται κάπως αλλιώς; Γιατί αν δείξω ότι είναι Παρ/μη μετά λογικά παίρνω f'(x)=-1/4 για τις δύο παραγώγους και βρίσκω 2-3 σημεία.
Καλή χρονιά!

Για ποιόν λόγο θέλεις να την βγάλεις εσύ παραγωγίσιμη στο 1 ;
Βρήκες οτι είναι παραγωγίσιμη σε μια ένωση διαστημάτων και επομένως προχωράς κανονικά λύνοντας την εξίσωση :

f'(x) = -1/4

Πρώτα για x>1 και μετά για x<1 (Αλλάζεις τον τύπο της f'(x) κάθε φορά όπως πρέπει) . Αφού βρεις τις τιμές των x που ικανοποιούν την παραπάνω,έστω x1,x2,τις βάζεις ανάλογα με το διάστημα που ανήκουν στον αντίστοιχο τύπο κλάδου που δίνεται απο τον ορισμό της f και βρίσκεις το f(x1) και το f(x2) . Έχεις την κλίση -1/4 και ένα σημείο για την κάθε ευθεία επομένως απο τον τύπο y-f(xo) = f'(xo)(x-xo) βρίσκεις τις ζητούμενες εξισώσεις πρώτα για xo=x1 και μετά για xo=x2 και f'(xo) = -1/4 .

Φυσικά πρέπει να δείξεις και τα βήματα που φανερώνουν οτι η f δεν είναι παραγωγίσιμη στο 1 και επομένως δεν μπορεί να είναι λύση το x=1 . Εαν έχεις κάποια απορία ακόμα πες μου,καλή χρονιά και σε εσένα !

 

[Papachrist]

Μπορεί κάποιος να μου στείλει χειρόγραφα το θέμα 4 στο Facebook .....αν μπορεί κάποιος να με εξυπηρετήσει θα τον ευχαριστούσα και θα το εκτιμούσα πολύ ευχαριστώ (fb name : john papagiannidis) φοράω μια μαύρη κουκούλα

 

[Samael]

Μπορεί κάποιος να μου στείλει χειρόγραφα το θέμα 4 στο Facebook .....αν μπορεί κάποιος να με εξυπηρετήσει θα τον ευχαριστούσα και θα το εκτιμούσα πολύ ευχαριστώ (fb name : john papagiannidis) φοράω μια μαύρη κουκούλα

Το Δ1 :

Spoiler

Χρησιμοποιήθηκε μια εκ των συνεπειών του Θ.Rolle για την απόδειξη .

Το Δ2 :

Spoiler

Αναλυτικός προσδιορισμός των επιμέρους παραστάσεων του αρχικού ορίου και εύρεση των ορίων τους . Οδηγούμαστε σε απροσδιοριστία 0*οο*0 οπότε αφήνουμε την τρίτη παράσταση ως έχει και προσπαθούμε να αποφανθούμε το όριο των 2 πρώτων παραστάσεων που είναι και ευκολότερο ώστε να καταλήξουμε στα επιμέρους όρια 0*0 = 0

DLH = Κανόνας L'Hôpital

Το Δ3 :

Spoiler

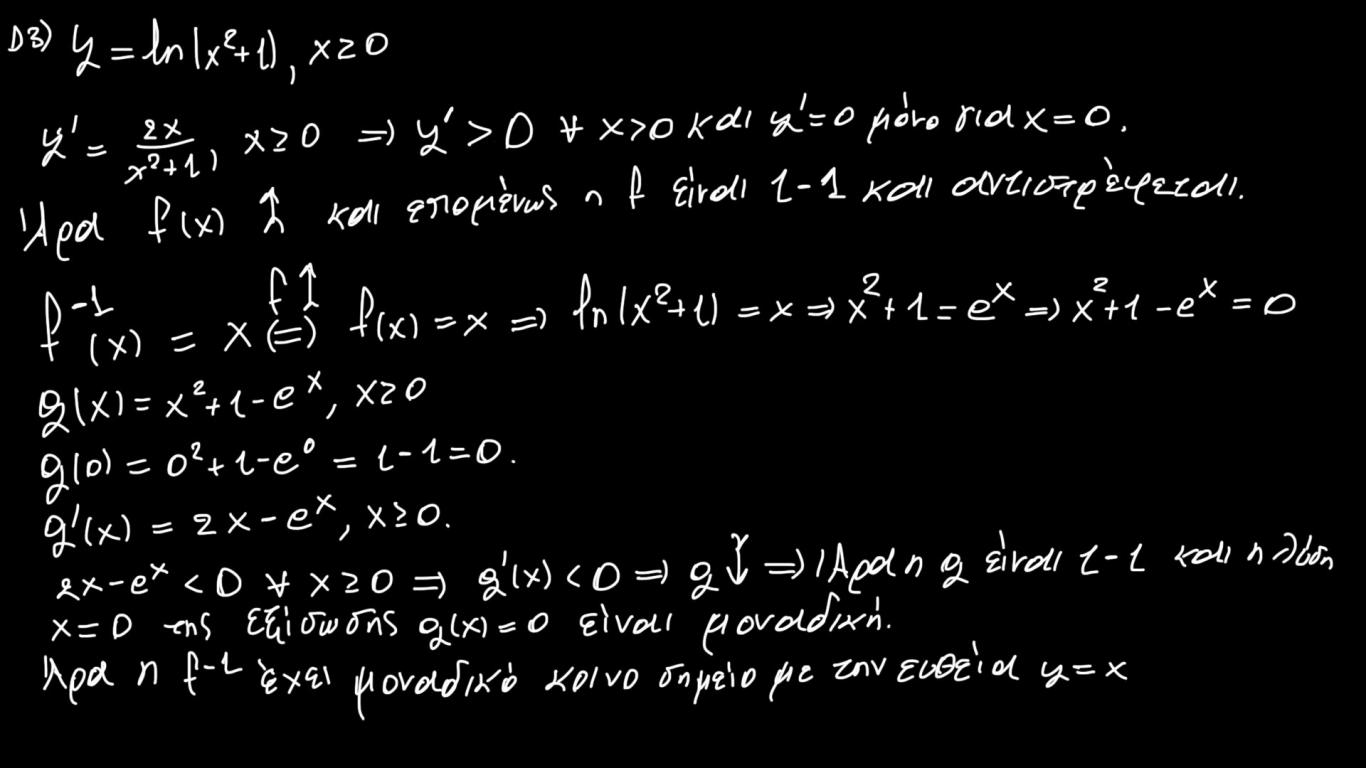
Προσοχή η ισοδυναμία της f-1(x)=x <=> f(x) = x ισχύει μόνο εφόσον η f είναι γνησίως αύξουσα(όπως και συμβαίνει σε αυτή την άσκηση) .

Το Δ4 :

Spoiler

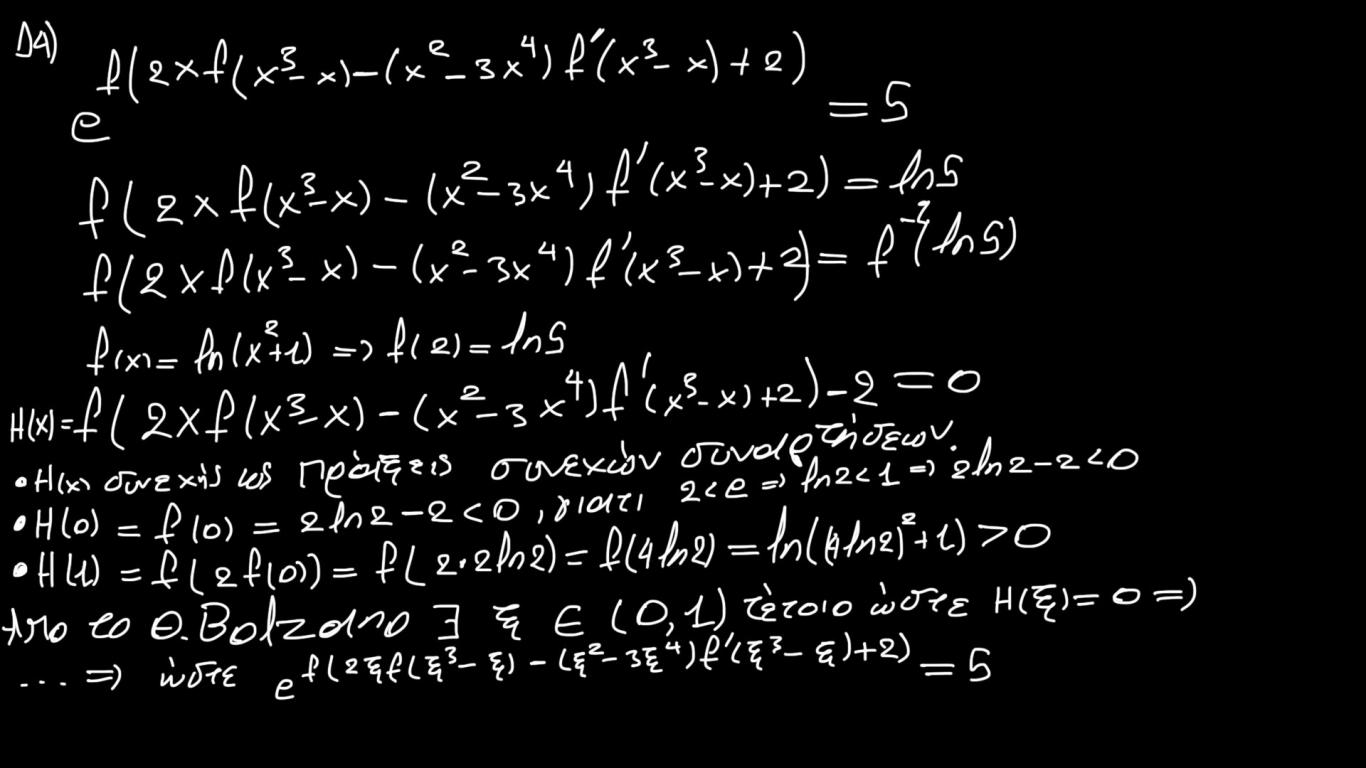
Τέθηκε συνάρτηση H(x) και εφαρμόστηκε το θεώρημα Bolzano . Επίσης υπολογίσαμε το f-1(ln5) ίσο με 2 αφού f(2) = ln5 . Δεν γίνεται αναλυτικός υπολογισμός των παραστάσεων εκ των προτέρων, παρα μόνο όταν είναι πλήρως απαραίτητο για το Θ.Bolzano καθώς ο έλεγχος σε συγκεκριμένες τιμές απλοποιεί αρκετά ότι χρειάζεται να υπολογίσουμε .

 

[Athens2002]

Το Δ1 :

Spoiler

Χρησιμοποιήθηκε μια εκ των συνεπειών του Θ.Rolle για την απόδειξη .

Το Δ2 :

Spoiler

Αναλυτικός προσδιορισμός των επιμέρους παραστάσεων του αρχικού ορίου και εύρεση των ορίων τους . Οδηγούμαστε σε απροσδιοριστία 0*οο*0 οπότε αφήνουμε την τρίτη παράσταση ως έχει και προσπαθούμε να αποφανθούμε το όριο των 2 πρώτων παραστάσεων που είναι και ευκολότερο ώστε να καταλήξουμε στα επιμέρους όρια 0*0 = 0

DLH = Κανόνας L'Hôpital

Το Δ3 :

Spoiler

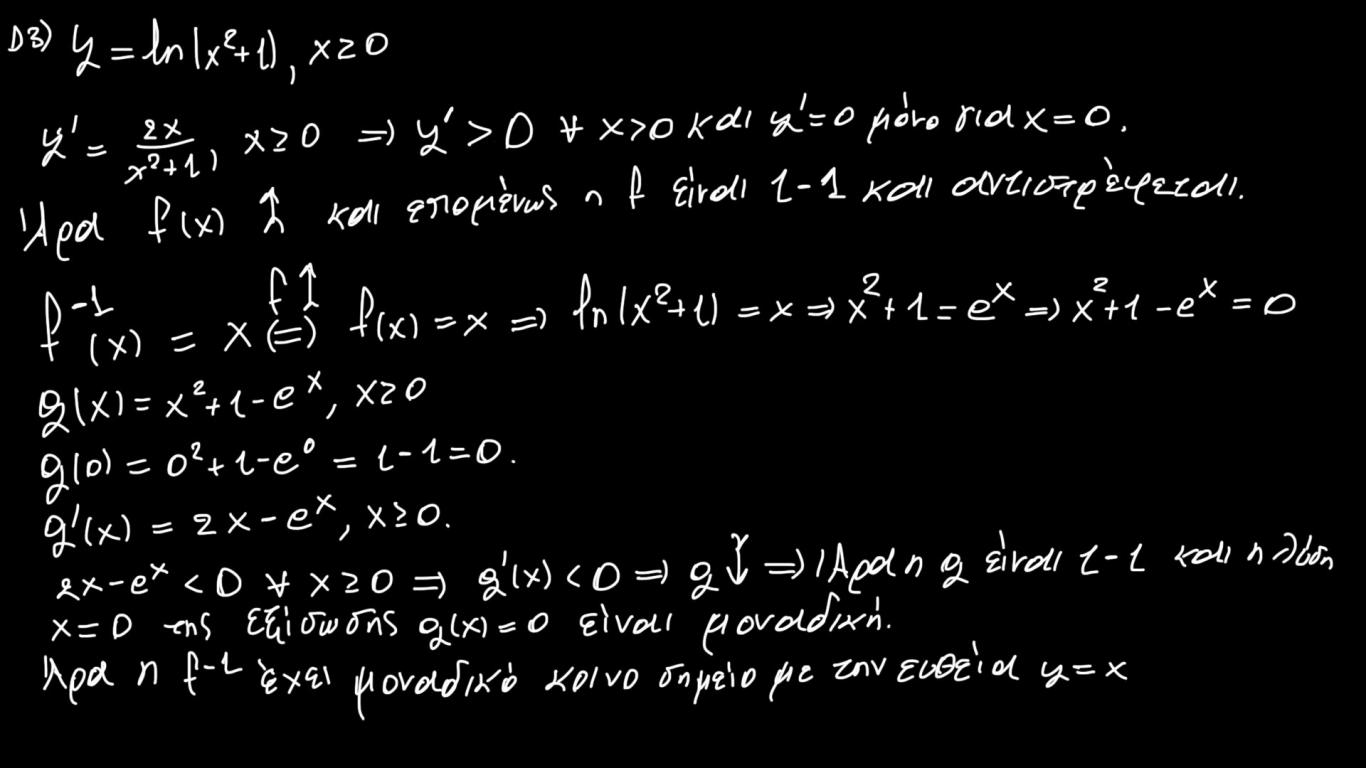
Προσοχή η ισοδυναμία της f-1(x)=x <=> f(x) = x ισχύει μόνο εφόσον η f είναι γνησίως αύξουσα(όπως και συμβαίνει σε αυτή την άσκηση) . Η ισοδυναμία ισχύει για οποιαδήποτε συνάρτηση αντιστρέφεται.


Το Δ4 :

Spoiler

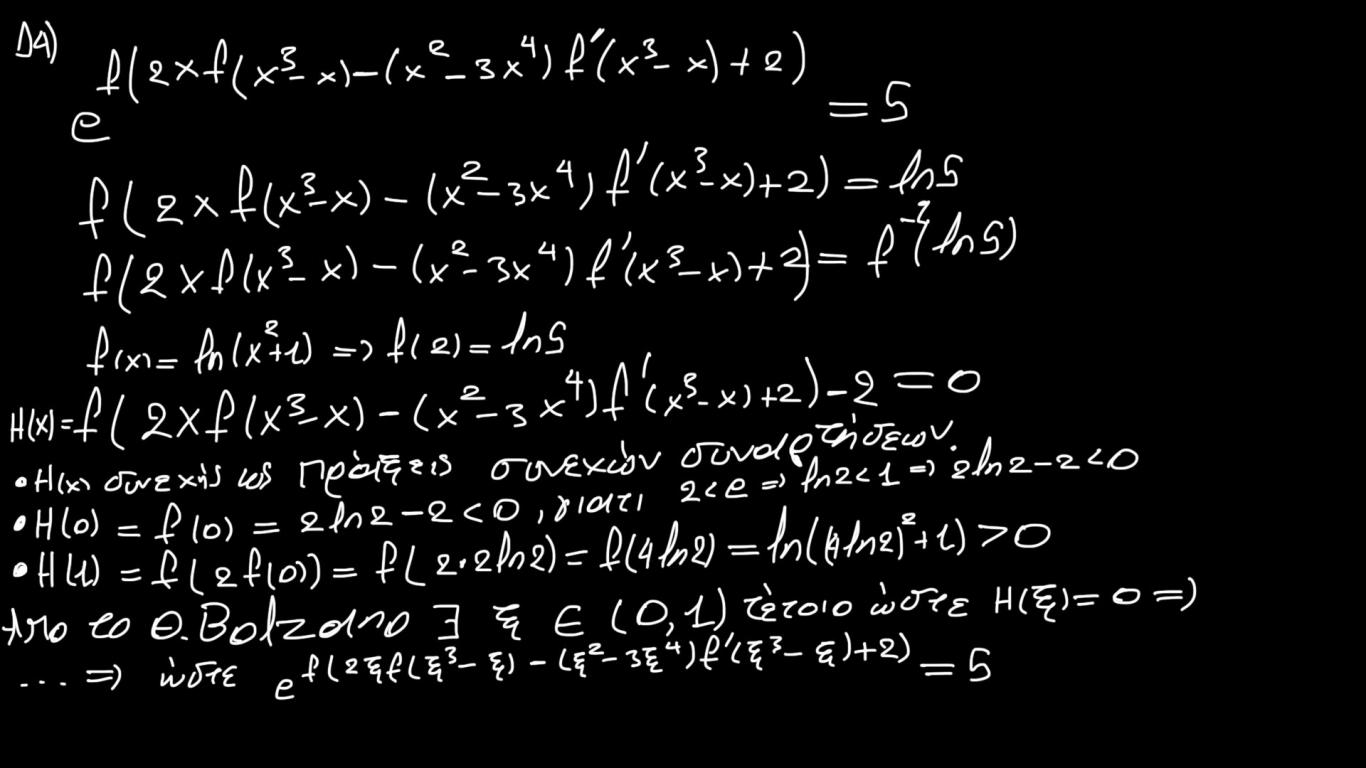
Τέθηκε συνάρτηση H(x) και εφαρμόστηκε το θεώρημα Bolzano . Επίσης υπολογίσαμε το f-1(ln5) ίσο με 2 αφού f(2) = ln5 . Δεν γίνεται αναλυτικός υπολογισμός των παραστάσεων εκ των προτέρων, παρα μόνο όταν είναι πλήρως απαραίτητο για το Θ.Bolzano καθώς ο έλεγχος σε συγκεκριμένες τιμές απλοποιεί αρκετά ότι χρειάζεται να υπολογίσουμε .

Αυτή η ισοδυναμία ισχύει μόνο για τις αύξουσες συναρτήσεις
f (x)=f-1 (x) <=> f (x)=x

 

[Samael]

Αυτή η ισοδυναμία ισχύει μόνο για τις αύξουσες συναρτήσεις
f (x)=f-1 (x) <=> f (x)=x

Σωστό πράγματι .

 

[Bill22]

Καλημέρα σας.

Δυσκολεύομαι να καταλάβω τη λύση της συγκεκριμένης εφαρμογής. (Μαθηματικά κατεύθυνσης Γ λυκείου, Β μέρος, σελ. 16, εφαρμογή ii) )
Η λύση είναι: (0,e]

Δεν καταλαβαίνω γιατί δεν θα μπορούσε να ισχύει π.χ. χ=10 αφού ln10=1. Μπορεί κάποιος να με βοηθήσει να καταλάβω που το χάνω;

 

[Papachrist]

.
Θα μπορούσατε να μου στείλετε τις λύσεις των ασκήσεων σήμερα παρακαλώ....θα το εκτιμούσα πολύ

 

[Μάρκος Βασίλης]

Θα μπορούσατε να μου στείλετε τις λύσεις των ασκήσεων σήμερα παρακαλώ....θα το εκτιμούσα πολύ

Να ρωτήσω τι έχεις προσπαθήσει ή αν έχει κάποια συγκεκριμένη απορία; Γιατί, δεν ξέρω που θα σε βοηθήσει να σου λύσει απλώς κάποιο άλλο άτομο τις ασκήσεις σου. Ειδικά, μάλιστα, με deadline...

 

[Papachrist]

Να ρωτήσω τι έχεις προσπαθήσει ή αν έχει κάποια συγκεκριμένη απορία; Γιατί, δεν ξέρω που θα σε βοηθήσει να σου λύσει απλώς κάποιο άλλο άτομο τις ασκήσεις σου. Ειδικά, μάλιστα, με deadline...

Το deadline είναι διότι έχω κάποιο οικογενειακό πρόβλημα και δεν έχω χρόνο .....αν μπορέσει κάποιος να με εξυπηρετήσει θα το εκτιμούσα...δεν θα πω εδώ τα προσωπικά μου.... ευχαριστώ και καλή συνέχεια

 

[Scandal]

Το deadline είναι διότι έχω κάποιο οικογενειακό πρόβλημα και δεν έχω χρόνο .....αν μπορέσει κάποιος να με εξυπηρετήσει θα το εκτιμούσα...δεν θα πω εδώ τα προσωπικά μου.... ευχαριστώ και καλή συνέχεια

Papachrist αν οι ασκήσεις είναι για το φροντιστήριο, εγώ πιστεύω ότι αν τους το πεις δεν θα σου πουν κάτι. Το φροντιστήριο είναι πρωτίστως για να σε βοηθήσει κι όχι να σε επιβαρύνει. Εμάς ο μαθηματικός δεν μας πίεζε να κάνουμε τις ασκήσεις για το σπίτι αν δεν μπορούσαμε για οποιονδήποτε λόγο. Αν είναι για το σχολείο τότε ok μπορεί να υπάρχει η ανησυχία για το βαθμό του τετραμήνου.

Προς θεού κανείς δεν θέλει να σε αποθαρρύνει από το να ζητάς βοήθεια σε ασκήσεις σου εδώ στο iSchool, απλά η μεγάλη ποσότητα ασκήσεων ενώ φαίνεται ότι δεν έχει αφιερωθεί / δεν μπορεί να αφιερωθεί χρόνος δίνει την εντύπωση ότι ζητείται βοήθεια απλά για να δείξεις στον καθηγητή ότι ασχολήθηκες (κι εδώ είναι που θέλω να σου πω ότι τον καθηγητή τον νοιάζει να βοηθηθείς εσύ κι όχι να ικανοποιηθεί ο ίδιος βλέποντας σε να έχεις λυμένες ασκήσεις).

Καλή επιτυχία με το ζόρι των πανελληνίων!!

 

[Papachrist]

Papachrist αν οι ασκήσεις είναι για το φροντιστήριο, εγώ πιστεύω ότι αν τους το πεις δεν θα σου πουν κάτι. Το φροντιστήριο είναι πρωτίστως για να σε βοηθήσει κι όχι να σε επιβαρύνει. Εμάς ο μαθηματικός δεν μας πίεζε να κάνουμε τις ασκήσεις για το σπίτι αν δεν μπορούσαμε για οποιονδήποτε λόγο. Αν είναι για το σχολείο τότε ok μπορεί να υπάρχει η ανησυχία για το βαθμό του τετραμήνου.

Προς θεού κανείς δεν θέλει να σε αποθαρρύνει από το να ζητάς βοήθεια σε ασκήσεις σου εδώ στο iSchool, απλά η μεγάλη ποσότητα ασκήσεων ενώ φαίνεται ότι δεν έχει αφιερωθεί / δεν μπορεί να αφιερωθεί χρόνος δίνει την εντύπωση ότι ζητείται βοήθεια απλά για να δείξεις στον καθηγητή ότι ασχολήθηκες (κι εδώ είναι που θέλω να σου πω ότι τον καθηγητή τον νοιάζει να βοηθηθείς εσύ κι όχι να ικανοποιηθεί ο ίδιος βλέποντας σε να έχεις λυμένες ασκήσεις).

Καλή επιτυχία με το ζόρι των πανελληνίων!!

Δεν είναι έτσι φίλε μου ξέρω ότι φαίνεται έτσι αλλά δεν είναι αυτη η πραγματικότητα ....τις ασκήσεις τις έχω προσπαθήσει αλλά λόγω μια οικογενειακής τραγωδίας δεν βγαίνουν με τίποτα ....για αυτό ζητάω βοήθεια από εδώ

 

[aggelosst9]

f(x)=x/e^(1/x)
Πρέπει να βρω ασύμπτωτες για να σχεδιάζω την Cf. Αν μπορεί κάποιος ας τις βρει και να εξηγήσει λίγο πως ακριβώς βγαίνουν τα όρια γιατί μπερδεύομαι αρκετά. Πχ πότε το 1/άπειρο κάνει άπειρο και πότε 0. Θα είμαι ΥΠΟΧΡΕΟΣ!!

 

[Samael]

f(x)=x/e^(1/x)
Πρέπει να βρω ασύμπτωτες για να σχεδιάζω την Cf. Αν μπορεί κάποιος ας τις βρει και να εξηγήσει λίγο πως ακριβώς βγαίνουν τα όρια γιατί μπερδεύομαι αρκετά. Πχ πότε το 1/άπειρο κάνει άπειρο και πότε 0. Θα είμαι ΥΠΟΧΡΕΟΣ!!

Διάβασε αυτά προτού συνεχίσεις για να καταλαβαίνεις τι συμβαίνει :

Spoiler

Παρατήρησα οτι έχεις μια δυσκολία για το πως βγαίνουν τα στοιχειώδη όρια . Έστω μια σταθερά Α Ε R και μια συνάρτηση g(x) . Έστω και ένα σημείο xo στο οποίο ξέρεις οτι :

lim g(x) = +-oo
x->xo

Τότε θα ισχύει :

lim A/g(x) = 0
x->xo

Το xo μπορεί να είναι οποιοσδήποτε πραγματικός αριθμός ή και το ίδια τα +οο ή -οο .

Εαν το όριο :

lim g(x) = 0
x->xo

και g(x) >= 0 για xo >= 0, τότε :

lim A/g(x) = +oo
x->xo+

Εαν ήταν g(x) <= 0 για xo >= 0 ,τότε :

lim A/g(x) = -oo
x->xo+

Ομοίως ανάλογα το πρόσημο της f αριστερά του xo( δηλαδή εαν f(x)<=0 ή f(x)>=0 για xo<=0) έχουμε :

lim A/g(x) = +oo , εαν f(x) >= 0
x->xo-

lim A/g(x) = -oo , εαν f(x) <= 0
x->xo-

Κάτι το οποίο είναι λογικό καθώς εαν σκεφτείς οτι έχεις 1/x καθώς το x->0+ φαντάσου οτι έχεις διαδοχικά αριθμούς : 1/0.01 , 1/0.001 , 1/0.0001 που σταδιακά σε οδηγούν στο +οο . Εαν όμως x-> 0- έχεις :
1/-0.01, 1/-0.001 , 1/-0.001 που σταδιακά σε οδηγούν στο -οο .

Λοιπόν,καταρχάς η συνάρτηση σου έχει πεδίο ορισμού το Df = R* = {x : x E R ^ x=!0 } = (-oo,0)U(0,+oo)
Επομένως είναι φυσικό να αναζητήσεις κατακόρυφη ασύμπτωτη στο x = 0 αφού είναι ένα σημείο στα άκρα του διαστήματος του πεδίου ορισμού της συνάρτησης f(x) .

Κατακόρυφες Ασύμπτωτες

Spoiler

Πρέπει να πάρουμε δύο όρια επομένως καθώς η συνάρτηση ορίζεται αμφότερα δεξιά και αριστερά του 0 . Ένα όριο πλησιάζοντας το 0 απο τα αριστερά,δηλαδή απο μικρότερες τιμές και ένα όριο απο τα δεξιά,δηλαδή πλησιάζοντας το 0 απο μεγαλύτερες τιμές . Ψάχνουμε άρα τα :

lim f(x) = L1
x->0+

lim f(x) = L2
x->0-

Για να υπολογίσουμε το όριο θα θέσουμε 1/x = u , οπότε x = 1/u .

x-> 0+ => u-> +oo στο L1
x-> 0- => u-> -oo στο L2

Σύμφωνα με τα παραπάνω η συνάρτηση μέσα στα όρια εκφράζεται κοινά και για τα δύο όρια ως προς u ως εξής:

f(x) = 1/ue^u

Το L1 = 0

Στο L2 έχουμε το θέμα οτι η e^u στον παρανομαστή τείνει στο 0 και η u στο -οο . Το οποίο είναι απροσδιόριστο .
Επομένως γράφουμε καλύτερα την συνάρτηση μέσα στο όριο ως : e^-u/u . Τώρα τo ζήτημα δεν έχει επιλυθεί καθώς το όριο της προηγούμενης ποσότητας καθώς το u τείνει στο -οο είναι +oo/-oo που είναι επίσης απροσδιόριστο . Ωστόσο είμαστε σε θέση να χρησιμοποιήσουμε τον κανόνα του L'Hospital και παραγογίζοντας ξεχωριστά αριθμητή και παρανομαστή ταυτόχρονα έχουμε :

Αριθμητής = (e^-u)' = -e^(-u) και παρανομαστής = (u)' = 1

Οπότε θέλουμε το όριο της συνάρτησης -e^(-u)/1 καθώς u -> -oo . Το οποίο φυσικά μας κάνει -οο .
Επομένως η συνάρτηση δεν έχει κατακόρυφη ασύμπτωτη στο 0+ αλλά έχει στο 0-

Πλάγιες ασύμπτωτες

Spoiler

Η δουλειά μας ωστόσο δεν έχει τελειώσει καθώς πρέπει να αναζητήσουμε πλάγιες ή οριζόντιες ασύμπτωτες . Βέβαια η ύπαρξη του ενός είδους αποκλείει στο +οο ή στο -οο την ύπαρξη του άλλου είδους .

Η θεωρία λοιπόν λέει οτι η συνάρτηση που μας ενδιαφέρει έχει πλάγια ασύμπτωτη στο +οο(αντίστοιχα στο -οο) εαν και μόνο εαν :

lim f(x)/x = λ
x->+oo

lim [f(x)-λx] = β
χ->+οο

(Αντίστοιχα όρια για το -οο) και θα είναι η y = λx+β

Πάμε να το δούμε στην πράξη . Η συνάρτηση μας είναι η f(x) = x/e^(1/x) .

Εύρεση λ στο +οο και - οο

Spoiler

Άρα με ενδιαφέρει το όριο της : x/x*e^(1/x) = 1/e^(1/x) καθώς το x->+oo και καθώς το x->-oo . Δηλαδή ψάχνουμε τα όρια :

lim 1/e^(1/x)
x->+oo

lim 1/e^(1/x)
x->-oo

Εφαρμόζω τον προηγούμενο μετασχηματισμό x = 1/u και έχω :

x-> +oo => u -> 0+
x-> -oo => u -> 0-

Στην προκειμένη τα όρια που ψάχνουμε είναι τα :

lim 1/e^u = λ1
u->0+

lim 1/e^u = λ2
u->0-

Όπου λ1 ο συντελεστής διεύθυνσης της ευθείας (εαν υπάρχει το όριο) στο +οο και λ2 ο συντελεστής διεύθυνσης της ευθείας στο -οο αντίστοιχα .

Και στις δύο περιπτώσεις για u = 0, τα όρια έχουν τιμή 1 .
Άρα λ1 = λ2 = 1

Εύρεση β στο +οο και - οο

Spoiler

Πρέπει να βρούμε τώρα και τιμές για τα όρια :

lim [f(x) - λ1χ] = β1
x->+oo

lim [f(x)-λ2x] = β2
x->-oo

Δηλαδή τα :

lim [x/e^(1/x) - χ] = β1
x->+oo

lim [x/e^(1/x) - x] = β2
x->-oo

Αυτά τα όρια δεν πρέπει να απειρίζονται ,διαφορετικά δεν υπάρχει πλάγια ασύμπτωτη στο +οο ή αντίστοιχα στο -οο.
Αντικαθιστούμε στην f(x) τον μετασχηματισμένο τύπο και έχουμε για την συνάρτηση μέσα στα όρια :
(Θυμήσου οτι u = 1/x => x = 1/u)

1/ue^u - 1/u = (1-e^u)/ue^u

Επειδή τα όρια έχουν την μορφή 0/0 εφαρμόζουμε τον κανόνα του L'Hospital και πάλι οπότε έχουμε παραγογίζοντας ξεχωριστά και ταυτόχρονα αριθμητή και παρανομαστή :

-e^u/(e^u+ue^u) = -e^u/[e^u(1+u)] = -1/(1+u)

Είτε για u->0+ είτε u->0- (τα όρια του u είναι τα ίδια με πριν αφού τα x τρέχουν πάλι στο +οο και -οο αντίστοιχα) τα όρια είναι :

β1 = β2 = -1

Τόσο στο +οο όσο και στο -οο η f(x) έχει πλάγια ασύμπτωτη την ίδια ευθεία : y = x - 1 .

Αποτελέσματα και γραφική παράσταση

Spoiler

Συνοψίζοντας :
1) Κατακόρυφη ασύμπτωτη στο x = 0-
2) Πλάγιες ασύμπτωτες στο +οο και στο -οο την y = x-1

Προσοχή πρέπει να δοθεί στο σημείο οτι δεν χρειάστηκε να ψάξουμε για οριζόντιες ασύμπτωτες στο +οο και -οο καθώς όπως είπα και νωρίτερα,εφόσον βρήκαμε πλάγιες ασύμπτωτες,δεν μπορούν να υπάρχουν οριζόντιες . Εαν στο +οο ή στο -οο ή και στα δυο βρίσκαμε λ = 0 σημαίνει οτι θα είχαμε οριζόντια ασύμπτωτη και θα έπρεπε να την βρούμε παίρνοντας το όριο :

lim f(x)
x-> +oo ή -οο

Ορίστε και μία φωτογραφία της f(x) για να καταλάβεις καλύτερα :

Η κόκκινη ευθεία είναι η y = x-1 και η μωβ κατακόρυφη ασύμπτωτη της f καθώς πλησιάζει το χ το 0 απο μικρότερες τιμές,δηλαδή αρνητικές . Παρατηρείς οτι πράγματι είναι ασύμπτωτες της f( η πράσσινη καμπύλη) .

Ελπίζω να βοήθησα,εαν έχεις κάποια απορία πες μου .

 

[Μάρκος Βασίλης]

@Samael Ένα σχόλιο για τις κατακόρυφες ασύμπτωτες και τα όρια, για να μην υπάρχουν παρανοήσεις.

Δεν υπάρχει κατακόρυφη στο 0+ και κατακόρυφη στο 0- (ούτε στα μαθηματικά ούτε στο σχολικό βιβλίο). Η γραφική παράσταση μίας συνάρτησης f έχει κατακόρυφη ασύμπτωτη σε ένα σημείο α του πεδίου ορισμού της αν τουλάχιστον ένα από τα δύο πλευρικά είναι άπειρο (οποιοδήποτε από τα δύο άπειρα). Επομένως, όταν μας βγαίνει το ένα πλευρικό και μας ζητείται μόνο ασύμπτωτη, δε χρειάζεται να το ψάξουμε παραπάνω - εδώ που ήθελε τη γραφική παράσταση, θα το υπολογίζαμε ούτως ή άλλως, βέβαια.

Επίσης, για τις πλάγιες και τις οριζόντιες, ο διαχωρισμός σε πλάγιες και οριζόντιες ασύμπτωτες γίνεται στο σχολικό βιβλίο για διδακτικούς σκοπούς - ορθώς γίνεται. Πρακτικά, ο ορισμός και τα θεωρήματα είναι τα ίδια - απλώς παίρνεις λ=0.

Σε σχέση τώρα με τα όρια, το πρόβλημα δεν είναι μόνο αν απειρίζεται ένα όριο, αλλά αν υπάρχει, εν γένει - το λέω για τα "β" αυτό. Για παράδειγμα το όριο

(μηδενική επί φραγμένη) οπότε λες λ=0, ενώ το όριο:

δεν υπάρχει - χωρίς όμως να απειρίζεται ή κάτι τέτοιο, υπάρχει ουσιώδες πρόβλημα στα άπειρα.

Κατά τα άλλα, άψογος!

 

[Samael]

@Samael Ένα σχόλιο για τις κατακόρυφες ασύμπτωτες και τα όρια, για να μην υπάρχουν παρανοήσεις.

Δεν υπάρχει κατακόρυφη στο 0+ και κατακόρυφη στο 0- (ούτε στα μαθηματικά ούτε στο σχολικό βιβλίο). Η γραφική παράσταση μίας συνάρτησης f έχει κατακόρυφη ασύμπτωτη σε ένα σημείο α του πεδίου ορισμού της αν τουλάχιστον ένα από τα δύο πλευρικά είναι άπειρο (οποιοδήποτε από τα δύο άπειρα). Επομένως, όταν μας βγαίνει το ένα πλευρικό και μας ζητείται μόνο ασύμπτωτη, δε χρειάζεται να το ψάξουμε παραπάνω - εδώ που ήθελε τη γραφική παράσταση, θα το υπολογίζαμε ούτως ή άλλως, βέβαια.

Επίσης, για τις πλάγιες και τις οριζόντιες, ο διαχωρισμός σε πλάγιες και οριζόντιες ασύμπτωτες γίνεται στο σχολικό βιβλίο για διδακτικούς σκοπούς - ορθώς γίνεται. Πρακτικά, ο ορισμός και τα θεωρήματα είναι τα ίδια - απλώς παίρνεις λ=0.

Σε σχέση τώρα με τα όρια, το πρόβλημα δεν είναι μόνο αν απειρίζεται ένα όριο, αλλά αν υπάρχει, εν γένει - το λέω για τα "β" αυτό. Για παράδειγμα το όριο

(μηδενική επί φραγμένη) οπότε λες λ=0, ενώ το όριο:

δεν υπάρχει - χωρίς όμως να απειρίζεται ή κάτι τέτοιο, υπάρχει ουσιώδες πρόβλημα στα άπειρα.

Κατά τα άλλα, άψογος!

Πράγματι το κατακόρυφη ασύμπτωτη στο 0- ή 0+ αποτελεί ξεκάθαρα δική μου αλχημεία .
Το σωστό είναι όπως λες κατακόρυφη ασύμπτωτη στο 0 και τελείωσε το θέμα !

Ευχαριστώ για την αναφορά σου στην σημαντική περίπτωση ανυπαρξίας του ορίου , την ξέχασα !
Όσο για την πλάγια εφαπτομένη,πράγματι έτσι είναι . Και εγώ μέχρι σήμερα θυμόμουν οτι το βιβλίο τα είχε ως δυο διαφορετικές περιπτώσεις ενώ επι της ουσίας , κοιτάζοντας την σχετική θεωρία πάλι σήμερα , παρατήρησα οτι η οριζόντια είναι απλά μια εκφυλισμένη περίπτωση της πλάγιας . Προσωπικά θα προτιμούσα αυτή την ερμηνεία,τώρα εαν κάποιος θέλει να τα αντιμετωπίζει διαφορετικά αυτά τα δύο οτι τον βολεύει καλύτερα υποθέτω,ωστόσο είναι τα ίδια πράγματα .

 

[aggelosst9]

Ευχαριστώ πάρα πολύ, ήσουν κατατοπιστικότατος και ξεκαθάρισα (νομίζω) αρκετά πράγματα. Και πάλι ευχαριστώ