Katerinaa
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Scandal
Διαχειριστής



Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Κατι θα κανωΟ @Samael λογικά μπορεί να σε βοηθήσει.
 .
.Καλησπέρα παιδιά, έχω αύριο να παραδώσω για το σχολείο κάποιες ασκήσεις και αυτή είναι η μόνη που δεν μου βγαίνει. Κάθε βοήθεια καλοδεχούμενη. Στις εικόνες φαίνεται ο τρόπος με τον οποίο έχω κινηθεί, χωρίς παρ'όλα αυτά να καταλήγω στο ζητούμενο.. Ευχαριστώ όλους εκ των προτέρων!!
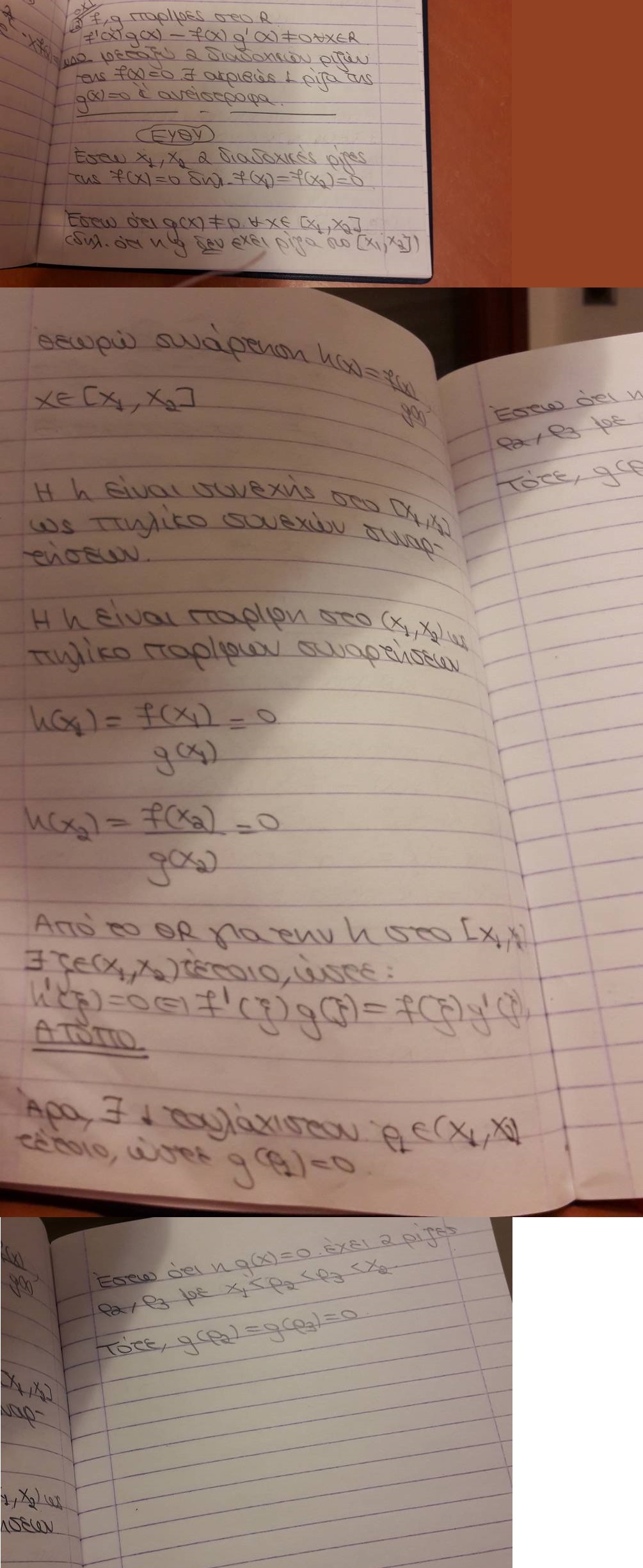
Ωραια το πηγες,εχω καποιες επιφυλαξεις για το πηλικο μεν αλλα τελος παντων προς το παρων το αφηνω γιατι δεν νομιζω να ειναι θεμα(σιγουρεψου ομως οτι η σχεση που σου δινεται εχει πραγματι πλην και οχι +)
Εφοσον βρηκες τουλαχιστον μια ριζα αρκει να αποδειξεις την μοναδικοτητα της.
Εστω οτι υπαρχει και ρ2 Ε (x1,x2) τετοια ωστε g(ρ2)=0.
Θα ισχυει απο το Θ.Rolle για την g στο [x1,x2](λες οτι ειναι συνεχης και παρ/μη μπλα μπλα μπλα) :
g'(ξ) = 0 ,με ξ Ε (ρ1,ρ2).
Ομως ισχυει :
f'g-fg' =! 0 Για καθε x E R
Αρα για ξ η παραπανω δινει :
f'(ξ)g(ξ)-f(ξ)g'(ξ) = 0 =>
-f(ξ)g'(ξ) =! 0 =>
f(ξ)g'(ξ) =! 0
To f(ξ) δεν παιζει να ειναι 0 διοτι ειναι μεταξυ του ρ1 και ρ2 τα οποια ειναι μεταξυ των x1,x2 που αποτλεουν διαδοχικες ριζες της f,οποτε αναγκαστικα g'(ξ) =! 0 .
Αρα το Rolle μας οδηγει σε ατοπο,και το μονο σφαλμα που μπορει να εχουμε κανει ειναι να υποθεσουμε οτι η g εχει δευτερη ριζα. Αρα αποδειχθηκε η μοναδικοτητα της ριζας ρ1.
Δοκιμασε τωρα να το πας και αντιστροφα με δεδομενο οτι η g εχει μοναδικη ριζα και ισχυει η σχεση που σου δινεται,να δειξεις οτι f(x1)=f(x2) = 0
 .
.Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Jim_Pap
Εκκολαπτόμενο μέλος


Αφου απο θR βγαλαμε g'(ξ)=0 μετα γιατι μηδενιζεται το f'(ξ)g(ξ) και οχι το f(ξ)g'(ξ); Και μετα ποιο ειναι το ατοπο στο g'(ξ)=0;Κατι θα κανω.
Ωραια το πηγες,εχω καποιες επιφυλαξεις για το πηλικο μεν αλλα τελος παντων προς το παρων το αφηνω γιατι δεν νομιζω να ειναι θεμα(σιγουρεψου ομως οτι η σχεση που σου δινεται εχει πραγματι πλην και οχι +)
Εφοσον βρηκες τουλαχιστον μια ριζα αρκει να αποδειξεις την μοναδικοτητα της.
Εστω οτι υπαρχει και ρ2 Ε (x1,x2) τετοια ωστε g(ρ2)=0.
Θα ισχυει απο το Θ.Rolle για την g στο [x1,x2](λες οτι ειναι συνεχης και παρ/μη μπλα μπλα μπλα) :
g'(ξ) = 0 ,με ξ Ε (ρ1,ρ2).
Ομως ισχυει :
f'g-fg' =! 0 Για καθε x E R
Αρα για ξ η παραπανω δινει :
f'(ξ)g(ξ)-f(ξ)g'(ξ) = 0 =>
-f(ξ)g'(ξ) =! 0 =>
f(ξ)g'(ξ) =! 0
To f(ξ) δεν παιζει να ειναι 0 διοτι ειναι μεταξυ του ρ1 και ρ2 τα οποια ειναι μεταξυ των x1,x2 που αποτλεουν διαδοχικες ριζες της f,οποτε αναγκαστικα g'(ξ) =! 0 .
Αρα το Rolle μας οδηγει σε ατοπο,και το μονο σφαλμα που μπορει να εχουμε κανει ειναι να υποθεσουμε οτι η g εχει δευτερη ριζα. Αρα αποδειχθηκε η μοναδικοτητα της ριζας ρ1.
Δοκιμασε τωρα να το πας και αντιστροφα με δεδομενο οτι η g εχει μοναδικη ριζα και ισχυει η σχεση που σου δινεται,να δειξεις οτι f(x1)=f(x2) = 0.
Δεν βρισκω τη συνοχη οτι υπεθεσες g(x) διαφορο του 0 με το ατοπο.Μπορεις μηπως να μου το εξηγησεις;Καλησπέρα παιδιά, έχω αύριο να παραδώσω για το σχολείο κάποιες ασκήσεις και αυτή είναι η μόνη που δεν μου βγαίνει. Κάθε βοήθεια καλοδεχούμενη. Στις εικόνες φαίνεται ο τρόπος με τον οποίο έχω κινηθεί, χωρίς παρ'όλα αυτά να καταλήγω στο ζητούμενο.. Ευχαριστώ όλους εκ των προτέρων!!
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Πολυ καλη ασκηση.Εχω μερικες αποριες.
Αφου απο θR βγαλαμε g'(ξ)=0 μετα γιατι μηδενιζεται το f'(ξ)g(ξ) και οχι το f(ξ)g'(ξ); Και μετα ποιο ειναι το ατοπο στο g'(ξ)=0;
Δεν βρισκω τη συνοχη οτι υπεθεσες g(x) διαφορο του 0 με το ατοπο.Μπορεις μηπως να μου το εξηγησεις;
Δεν εχεις αδικο.Ισως το προβλημα μπορει να ξεπεραστει και θα σου εξηγησω και το αλλο σου ερωτημα.
Εχετε κανει ωστοσο ΘΜΤ και συνεπειες;
Τελος παντων δεν ξερω εαν το εχετε κανει οποτε θα παραθεσω εναλλακτικη :
Εστω οτι υπαρχει ριζα ρ2 τετοια ωστε g(ρ2) = 0 .
Πολλαπλασιαζοντας με πλην την αρχικη εχουμε :
f'g-fg' =! 0 =>
g'f-gf' =! 0 =>
θεωρω οτι ρ1<x<ρ2 και διαιρω με f².
Εχω οτι : (g/f)' =! 0 .
g/f συνεχης στο [ρ1,ρ2] & παρ/μη στο (ρ1,ρ2) ως πραξεις μεταξυ παραγωγισιμων συναρτησεων, με (g/f)(ρ1)=(g/f)(ρ2)=0 .
Απο το Θ.Rolle υπαρχει ξ Ε (ρ1,ρ2) τετοιο ωστε :
(g/f)'(ξ) = 0 => f'(ξ)g(ξ)-f(ξ)g'(ξ) = 0 Ατοπο.(Πολλαπλασιασαμε με f² για να αφησουμε μονο παρανομαστη).
Αρα η g δεν εχει αλλη ριζα.
Για να απαντησω και στο αλλο σου ερωτημα :
Πραγματι δεν φαινεται η συνδεση του ατοπου και μπραβο σου που την ειδες γιατι θελει κοφτερο ματι.Συνηθως υποσυνειδητα οι περισσοτεροι θα την περναμε ως δεδομενη,ακομα και εγω.Ειναι φανερο εξαλλου οτι ευκολα κανεις λογικα λαθη και ουτε που το παιρνεις χαμπαρι
 .Εκει που εγω καταλαβα οτι καπου θα υπαρξει "θολο" σημειο ειναι οταν εγινε η διαιρεση με την g η οποια ηταν αγνωστο ουσιαστικα εαν ειναι 0 η οχι,αλλα εμεις καναμε την υποθεση και προχωρησαμε χωρις να το διευκρινισουμε. Οποτε η αρχικη "αβεβαιοτητα" υπαρχει σε εκεινο το σημειο και εμφανιζεται και στο ατοπο αργοτερα.
.Εκει που εγω καταλαβα οτι καπου θα υπαρξει "θολο" σημειο ειναι οταν εγινε η διαιρεση με την g η οποια ηταν αγνωστο ουσιαστικα εαν ειναι 0 η οχι,αλλα εμεις καναμε την υποθεση και προχωρησαμε χωρις να το διευκρινισουμε. Οποτε η αρχικη "αβεβαιοτητα" υπαρχει σε εκεινο το σημειο και εμφανιζεται και στο ατοπο αργοτερα.Τα πραγματα εχουν ως εξης : Διαιρεις με το g,δεχομενος οτι δεν υπαρχει ριζα.
Αργοτερα καταληγεις σε ενα κλασμα με αριθμητη την σχεση που σου δινεται και παρανομαστη την g και μαλιστα το βγαζεις ισο με το 0.
Ο μονος τροπος να γινει κατι τετοιο ειναι ειτε,ο αριθμητης να ειναι μηδεν,μα αυτο ομως δεν ισχυει.
Αρα ατοπο.
Εχουμε κανει λαθος στην υποθεση του Θ.Rolle.
Δεχτηκαμε οτι η f/g ειναι παραγωγισιμη στο (x1,x2) . Δεχτηκαμε επισης οτι η f/g ειναι συνεχης στο [x1,x2] Σε ολες τις περιπτωσεις ενα απο αυτα πρεπει να ειναι λανθασμενη υποθεση και ειτε στο ενα ειτε στο αλλο ουσιαστικα,το προβληματικο σημειο θα ειναι οτι η g σε εκεινο το σημειο ειναι 0.
Δεχτηκαμε επισης οτι f(x1)=f(x2)=0 αλλα αυτα ξερουμε οτι ισχυουν γιατι δινονται απο την υποθεση.
Χρειαζεται αρκετη προσοχη καθως ειναι μια "sneaky" λυση απο την αρχη της,μεχρι να καταλαβεις που παει το πραγμα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Jim_Pap
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Πραγματικα ειναι μια ασκηση που θελει προσοχη. Εχω κανει συνεπειες ΘΜΤ. Θα λυνοταν κι αλλιως;
Το επεξεργαζομαι διοτι ειχα μια ιδεα χθες,αλλα εως τωρα δεν την κοβω να λειτουργει.
Βεβαια εαν καποιος εφαρμοζε το ΘΜΤ αντι για το Rolle στα ιδια διαστηματα με τις ιδιες συναρτησεις δεν θα ειχε θεμα,διοτι το Rolle ειναι ειδικη περιπτωση του ΘΜΤ.
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Katerinaa
Νεοφερμένο μέλος


 Samael με βοήθησες πάρα πολύ. Η λύση λοιπόν που παρέδωσα στον καθηγητή μου ήταν τελικά η εξής και μου είπε πως είναι ολόσωστη. Να διευκρινίσω σε αυτό το σημείο, ότι σχετικά με τις ενστάσεις που διατυπώθηκαν όσον αφορά στην υπόθεση που έκανα ότι το g(x)#0 για κάθε x που ανήκει στο [x1,x2] και τελικά κατέληξα σε άτοπο, δεν υφίσταται κάποιο θολό σημείο, εφόσον τελικά κατέληξα σε άτομο μέσω του Θ.Rolle. Επομένως, η συνάρτηση h(x)=f(x)/g(x) μπορεί να οριστεί άφοβα (έτσι τουλάχιστον μου είπε ο καθηγητής μου). Το λάθος το οποίο έκανα αρχικά, μιας και του έδειξα όλες μου τις απόπειρες και τους συλλογισμούς (και τους δικούς σας φυσικά
Samael με βοήθησες πάρα πολύ. Η λύση λοιπόν που παρέδωσα στον καθηγητή μου ήταν τελικά η εξής και μου είπε πως είναι ολόσωστη. Να διευκρινίσω σε αυτό το σημείο, ότι σχετικά με τις ενστάσεις που διατυπώθηκαν όσον αφορά στην υπόθεση που έκανα ότι το g(x)#0 για κάθε x που ανήκει στο [x1,x2] και τελικά κατέληξα σε άτοπο, δεν υφίσταται κάποιο θολό σημείο, εφόσον τελικά κατέληξα σε άτομο μέσω του Θ.Rolle. Επομένως, η συνάρτηση h(x)=f(x)/g(x) μπορεί να οριστεί άφοβα (έτσι τουλάχιστον μου είπε ο καθηγητής μου). Το λάθος το οποίο έκανα αρχικά, μιας και του έδειξα όλες μου τις απόπειρες και τους συλλογισμούς (και τους δικούς σας φυσικά  ), ήταν το ότι προσπάθησα να δείξω ότι η g(x)=0 έχει 2 ρίζες ρ2 και ρ3 και προσπαθούσα με κάποιον τρόπο να καταλήξω σε άτομο, στην προσπάθειά μου να αποδείξω τη μοναδικότητα της ρ1 που βρήκα αρχικά. Το λάθος έγκειται στο γεγονός ότι είναι αδύνατον να καταλήξω σε άτομο με αυτόν τον τρόπο, οπότε αναγκαστικά πρέπει να κινηθούμε αλλιώς. Ο σωστός τρόπος για την επίλυση της άσκησης από το σημείο που βρήκα ότι υπάρχει 1 τουλάχιστον ρ1 που ανήκει στο (x1,x2) ώστε g(ρ1)=0 και έπειτα είναι ΑΚΡΙΒΩΣ αυτός που επισήμανε ο Samael εν τέλει. Δηλαδή, είναι αναγκαίο να θεωρήσω τη συνάρτηση φ(x)=g(x)/f(x) και μέσω του Θ.Rolle να καταλήξω σε άτοπο.
), ήταν το ότι προσπάθησα να δείξω ότι η g(x)=0 έχει 2 ρίζες ρ2 και ρ3 και προσπαθούσα με κάποιον τρόπο να καταλήξω σε άτομο, στην προσπάθειά μου να αποδείξω τη μοναδικότητα της ρ1 που βρήκα αρχικά. Το λάθος έγκειται στο γεγονός ότι είναι αδύνατον να καταλήξω σε άτομο με αυτόν τον τρόπο, οπότε αναγκαστικά πρέπει να κινηθούμε αλλιώς. Ο σωστός τρόπος για την επίλυση της άσκησης από το σημείο που βρήκα ότι υπάρχει 1 τουλάχιστον ρ1 που ανήκει στο (x1,x2) ώστε g(ρ1)=0 και έπειτα είναι ΑΚΡΙΒΩΣ αυτός που επισήμανε ο Samael εν τέλει. Δηλαδή, είναι αναγκαίο να θεωρήσω τη συνάρτηση φ(x)=g(x)/f(x) και μέσω του Θ.Rolle να καταλήξω σε άτοπο.



Πραγματικα ειναι μια ασκηση που θελει προσοχη. Εχω κανει συνεπειες ΘΜΤ. Θα λυνοταν κι αλλιως;
Ρώτησα τον καθηγητή μου εάν έβγαινε με συνέπειες του ΘΜΤ, καθώς εμένα δεν μου πέρασε με τίποτα από το μυαλό ένας τέτοιος τρόπος λύσης και μου είπε πως πιθανότατα δεν βγαίνει κατά τη γνώμη του, ή εάν βγει θα βγει μετά από πολύ κόπο.
Πολυ καλη ασκηση.Εχω μερικες αποριες.
Αφου απο θR βγαλαμε g'(ξ)=0 μετα γιατι μηδενιζεται το f'(ξ)g(ξ) και οχι το f(ξ)g'(ξ); Και μετα ποιο ειναι το ατοπο στο g'(ξ)=0;
Δεν βρισκω τη συνοχη οτι υπεθεσες g(x) διαφορο του 0 με το ατοπο.Μπορεις μηπως να μου το εξηγησεις;
Όσον αφορά στο πρώτο σου ερώτημα, πράγματι το f(ξ)g'(ξ) μηδενίζεται κινούμενοι με αυτόν τον τρόπο, και όχι το f'(ξ)g(ξ), επομένως έχει γίνει ένα λαθάκι εδώ, αλλά δεν υπάρχει πρόβλημα, μιας και δεν βγαίνει ούτως ή άλλως με αυτόν τον τρόπο.

Για τη δεύτερη ερώτησή σου, λόγω της σχέσης που μου δίνει η άσκηση, το μυαλό μου σκέφτηκε κατευθείαν πως αυτή μοιάζει (εάν υπήρχε στον παρονομαστή και ένα g τετράγωνο του x), οπότε αμέσως σκέφτηκα να ορίσω τη συνάρτηση h(x)= f(x)/g(x) , της οποίας η παράγωγος είναι η δοθείσα σχέση της άσκησης. Όμως, για να έχω εγώ το δικαίωμα να ορίσω μία συνάρτηση με παρονομαστή το g(x), πρέπει να είμαι σίγουρη ότι g(x)#0. Αφού δεν μπορώ να εξάγω κάτι τέτοιο από τα δεδομένα της άσκησης, το υποθέτω. Λέω ΕΣΤΩ ότι ισχύει και με Rolle καταλήγω σε άτοπο. Άρα, δεν υπάρχει κανένα x που να ανήκει στο διάστημα [x1,x2] το οποίο να είναι ρίζα της εξίσωσης g(x)=0. Συνεπώς, η g(x)=0 έχει ρίζα και συγκεκριμένα τουλάχιστον μία (λόγω Rolle). Όμως, εγώ θέλω να δείξω ότι η ρίζα αυτή είναι και μοναδική. Και εδώ με ζόρισε το πράγμα.
Ελπίζω να το εξήγησα όσο καλύτερα μπόρεσα, πιο πάνω ανάρτησα και τη λύση της άσκησης, όπως μου την εξήγησαν στο σχολείο.

Παρ'όλα αυτά, προσπάθησα αρχικά να τη λύσω και όπως είπε ο Samael αρχικά, αλλά δεν μπορούσα να καταλήξω σε άτοπο, οπότε πήγα όπως είπε τελικά και μου βγήκε πολύ καλά
 Ο τρόπος σκέψης είναι σίγουρα σωστός, απλά δεν νομίζω ότι κατέληγε κάπου ή ίσως να ήθελε περισσότερη δουλειά. Παραθέτω και αυτήν την "απόπειρα" λοιπόν για να έχουμε μια πιο σφαιρική εικόνα όλων των τρόπων με τους οποίους μπορούμε να κινηθούμε σε αυτήν την άσκηση
Ο τρόπος σκέψης είναι σίγουρα σωστός, απλά δεν νομίζω ότι κατέληγε κάπου ή ίσως να ήθελε περισσότερη δουλειά. Παραθέτω και αυτήν την "απόπειρα" λοιπόν για να έχουμε μια πιο σφαιρική εικόνα όλων των τρόπων με τους οποίους μπορούμε να κινηθούμε σε αυτήν την άσκηση 

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Katerinaa
Νεοφερμένο μέλος


Είμαι περίεργη να ακούσω την άποψή σας πάνω σε αυτό! Μόλις τώρα μου ήρθε στο μυαλό.
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Giorgos496
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Samael
Τιμώμενο Μέλος


Ισως καλο θα ηταν να διευκρινιστει απο το πρωτο ατοπο προκυπτει οτι η g εχει ριζει στο κλειστο [χ1, χ2] ομως τα ακρα απορριπτονται αφουν αν θεσουμε χ=χ1 ή χ=χ2 στη δοθεισα σχεση καταληγουμε σε ατοπο
Η ριζα ζητειται ουτως η αλλως στο ανοικτο διαστημα οποτε αυτο δεν ειναι απαραιτητο.
Αυτο που πηραμε λιγο ως δεδομενο και χρειαζεται επισης αποδειξη ειναι οτι :
g(x1)=!0
g(x2)=!0
Διοτι αργοτερα στο 1ο ατοπο η g ως παρανομαστης τις παιρνει αυτες τις τιμες.Αυτο προκυπτει ευκολα ανικαθιστωντας βεβαια οπως ειπες x=x1 & x=x2 στην αρχικη.Πρακτικα τοτε ειναι πληρης η αποδειξη.
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
American Economist
Επιφανές μέλος


Για κάθε χ>0 ισχύει ότι (α^χ)’= χ·α^χ-1;
Αν f’(x)=g’(x) για κάθε χ€R τότε f και g ίσες;
Αν για κάθε f ισχύει f’(x)=0 για κάθε x€R* τότε η f σταθερή σε όλο το R*?
Αν f παραγωγισιμη στο (α,β) και f(a)=f(β) και f’(x)#0 για κάθε χ€(α,β) τότε f όχι συνεχείς στο [α,β];
Μια βοήθεια σας παρακαλώ.
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Athens2002
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
American Economist
Επιφανές μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Lancelot
Περιβόητο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Jim_Pap
Εκκολαπτόμενο μέλος


Το πρωτο ειναι σιγουρο λαθος. Το a^x παραγωγιζεται ως (a^x)*lnaΕυχαριστώ το πρώτο ξέρεις;
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Giorgos496
Νεοφερμένο μέλος


Δευτερο λαθος απο συνεπειες θμτ
Τριτο λαθος αφου μπορει να αλλαζει τυπο
Τεταρτο σωστο
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
American Economist
Επιφανές μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Lancelot
Περιβόητο μέλος


Το πρωτο ειναι σιγουρο λαθος. Το a^x παραγωγιζεται ως (a^x)*lna
Το πρωτο λαθος αφου (α^x) '=lnα* α^x
Δευτερο λαθος απο συνεπειες θμτ
Τριτο λαθος αφου μπορει να αλλαζει τυπο
Τεταρτο σωστο
Τι μαλ#$@54 έγραψα .
Πωωω είδα χ^α
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 092312
Επισκέπτης


Παιδιά έχω 4 ΣΛ
1)Για κάθε χ>0 ισχύει ότι (α^χ)’= χ·α^χ-1;
2)Αν f’(x)=g’(x) για κάθε χ€R τότε f και g ίσες;
3)Αν για κάθε f ισχύει f’(x)=0 για κάθε x€R* τότε η f σταθερή σε όλο το R*?
4)Αν f παραγωγισιμη στο (α,β) και f(a)=f(β) και f’(x)#0 για κάθε χ€(α,β) τότε f όχι συνεχείς στο [α,β];
Μια βοήθεια σας παρακαλώ.
1) Λ
(a^x)'=a^x*lna
2) Λ
f'(x)=g'(x)<=>f(x)=g(x)+c, c εν R
3) Λ
Δεν ισχύει σε ένωση διαστημάτων, αντιπαράδειγμα να αλλάζει τύπο στο 0
4) Σ
Έστω προς άτοπο ότι f συνεχής στο [α,β]
Πληροί τις προϋποθέσεις για Rolle=>Jxο στο (a,b):f'(x0)=0
Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

