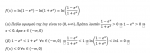Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[Guest 190013]

Φαντάζομαι ναι, αν και η απόδειξη είναι μισή γραμμή, δεν έχει πρακτικά διαφορά. Σε μια άσκηση δηλαδή μπορείς να την συμπεριλάβεις.

Εντιτ: Με το γράμμα του νόμου, αν δεν είναι στο σχολικό, είναι όπως τα λέει ο unseen.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Unseen skygge]

Νομίζω Όχι δεν μπορείς χωρίς απόδειξη έχω την εντύπωση δεν υπάρχει στο σχολικό.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Αγγελος Κοκ]

Καλησπερα! Μπορουμε να χρησιμοποιησουμε χωρις αποδειξη τα παρακατω;

Το ολοκλήρωμα κάθε περιττή συνάρτησης f(x) (f(-x)=-f(x)) με αντίθετα άκρα ολοκλήρωσης είναι μηδέν

Το ολοκλήρωμα κάθε άρτιας συνάρτησης f(x) (f(-x)=f(x)) με αντίθετα άκρα ολοκλήρωσης είναι ίσο με το διπλασιο ολοκληρωμα με ακρα 0 και α

Δεν ειναι στο σχολικο και επειδη δεν υπαρχει εστω και σαν εφαρμογη στο σχολικο οχι δεν μπορεις

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[kachorra]

Ευχαριστω

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Happily.Motionless]

βοήθεια .... Στο β) βρίσκω e^x=0

Δίνεται η συνάντηση f(x)=ln(1- e^x) - ln(1+e^x)

A) πεδίο ορισμου
Β) πρόσημο f

Ολόκληρη η άσκηση

https://ibb.co/g2kSXG

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Lancelot]

Καλησπέρα και καλη χρονιά

Δεν σου βγήκε το προσημο απο το πεδιο ορισμου;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Αγγελος Κοκ]

βοήθεια .... Στο β) βρίσκω e^x=0

Δίνεται η συνάντηση f(x)=ln(1- e^x) - ln(1+e^x)

A) πεδίο ορισμου
Β) πρόσημο f

Ολόκληρη η άσκηση

https://ibb.co/g2kSXG

Η f(x) γραφεται και ως f(x)=ln[(1-e^x)/(1+e^x)]
Για να βρεις το προσημο της f πρεπει να λυσεις την f(x)=0<=>ln(1-e^x)=ln(1+e^x)<=>1-e^x=1+e^x<=>e^x=0 αδυνατο αρα η f δεν εχει ριζες
Επειδη η f ειναι συνεχης με f#0 διατηρει το προσημο
Ευκολα μπορει πλεον να αποδειξεις οτι η f ειναι μικροτερη του μηδενος για καθε χ που ανηκει στο πεδιο ορισμου της

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Lancelot]

https://www.desmos.com/calculator/sq1m2voivn

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Happily.Motionless]

Απλα εχω λιγο με το πςδιο ορισμου θεμα ... Το προσημο ναι σταθερο ...Πιο ορισμου ειναι μηπως AF =(-∞,0)u(0,+∞) ?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Lancelot]

Μονο εκει που ειναι θετικο θες
αρα (-απειρο,0)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Αγγελος Κοκ]

Απλα εχω λιγο με το πςδιο ορισμου θεμα ... Το προσημο ναι σταθερο ...Πιο ορισμου ειναι μηπως AF =(-∞,0)u(0,+∞) ?

Οταν εχεις λογαριθμικα πρεπει το μεσα να ειναι >0,οπως πολυ σωστα λεει και ο Lancelot
Δηλαδη: λυνεις τις 1+e^x>0 και 1-e^x>0.Το κοινο πεδιο λυσεων ειναι και το πεδιο ορισμου της f

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Happily.Motionless]

Ναι απλα το θεμα πιο ειναι ... Το ενα βγαινει χ<0 και το αλλο.... Αδυνατο?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

Η 1+e^x >0 ισχύει για κάθε πραγματικό χ, εφόσον το e^x είναι έτσι κι αλλιώς θετική ποσότητα.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[osfp123123]

Αν έχω f (x) μια δικλαδη με κλαδους:χ-1,αν χ <1 και χ-2 αν χ>1 πρέπει να εξετάσω αν η f είναι παραγωγισιμη στο 1??Ευχαριστώ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Unseen skygge]

Τι θες να βρεις μονοτονια;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[unπαικτable]

Η λυση...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Αγγελος Κοκ]

Αν έχω f (x) μια δικλαδη με κλαδους:χ-1,αν χ <1 και χ-2 αν χ>1 πρέπει να εξετάσω αν η f είναι παραγωγισιμη στο 1??Ευχαριστώ

Θυμασαι πως δειχνεις οτι μια δικλαδη συναρτηση ειναι συνεχης στο χ0; ε την ιδια διαδικασια κανεις μονο που δειχνεις οτι ειναι παραγωγισιμη στο χ0

1ος τροπος: Παρε τα ορια k=limx->1- [f(x)-f(1)]/[x-1] και u=limx->1+[f(x)-f(1)]/[x-1] και δες αν k=u,εR.Αν k=u,εR τοτε ειναι παραγωγισιμη στο χ0=1
Σημειωση limx->1- f(x)=limx->1- (x-1) και limx->1+ f(x)=limx->1+ (x-2)

2ος τροπος: Φαινεται και με το ματι οτι η f δεν ειναι συνεχης στο χ0=1.Εφοσον δεν ειναι συνεχης στο χ0=1 δεν ειναι και παραγωγισιμη στο χ0=1(δεν ισχυει υποχρεωτικα το αντιστροφο)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Samael]

Αν έχω f (x) μια δικλαδη με κλαδους:χ-1,αν χ <1 και χ-2 αν χ>1 πρέπει να εξετάσω αν η f είναι παραγωγισιμη στο 1??Ευχαριστώ

Σε αυτο προσεξε παρα πολυ διοτι ετσι την πατησαν πολλοι περυσι :

Εαν σου ζητησει μονοτονια ΔΕΝ εισαι υποχρεωμενος να εξετασεις την παραγωγισιμοτητα στο σημειο με τεμημενη χ =1.
Αρκει να βρεις το προσημο της 1ης παραγωγου στα εκατερωθεν γειτονικα/ο διαστημα και να βγαλεις πορισμα για την κλειστη μορφη του διαστηματος αφου ελεγξεις την συνεχεια στο 1 και στο αλλο ακρο του διαστηματος εαν οριζεται η f σε αυτο.

Εαν σου ζηταει η ασκηση να ελεγξεις την παραγωγισιμοτητα στο σημειο αυτο και δεν μπορεις να αποδειξεις οτι ειναι παραγωγισιμη,ειτε με τους κανονες ειτε με τον ορισμο της παραγωγο τοτε να ευχεσαι να μπορεις να αποδειξεις οτι δεν ειναι συνεχης ωστε να μην ειναι και παραγωγισιμη και να απαντησεις.Το αντιστροφο δεν ισχυει.

Εαν σου ζηταει τα κρισιμα σημεια της f(Τα εσωτερικα σημεια στα οποια η f δεν παραγωγιζεται η δεν υπαρχει η τα ακρα του διαστηματος εαν αυτο ειναι κλειστο διαστημα) τοτε πρεπει οπωσδηποτε να ελεγξεις παλι τι γινεται στο 1. Σε αυτη την περιπτωση μπορεις παλι να χρησιμοποιησεις το κολπο της περιπτωσης απο πανω.

Τα πανω καταλαβε τα καλα και δεν θα χασεις.
Για να απαντησω και στην ερωτηση σου.Ποτε εχει νοημα η αναζητηση της συνεχειας σε ενα σημειο;
Οταν αυτο ανηκει στο πεδιο ορισμου της συναρτησης.Εσενα οριζεται κατω απο το 1 και πανω απο το 1,αλλα κανενας απο τους δυο κλαδους δεν το περιεχει(ανισο-ισοτητα δηλαδη)
Μπορει να θεωρηθει λαθος ακομα και να ελεγξεις με πλευρικα ορια τι γινεται στο 1 διοτι δεν γινεται να ελεγξεις για κατι που ξερεις εξ'ορισμου οτι δεν υπαρχει,εκτος και εαν δεν εχεις διαβασει καλα την θεωρια(οποτε θα θεωρησει οτι αυτο συμβαινει και θα σου κοψει βαθμο ο βαθμολογητης ).
Δεν ξερω κατα ποσο καποιος θα ειναι τοσο σκληρος διοτι δεν ειναι απαραιτητα τραγικο λαθος καθως τεχνικα η διαδικασια εχει νοημα αφου υπαρχουν τα πλευρικα ορια.Ωστοσο ποτε δεν ξερεις.Αλλα ναι,εαν θες απαντας οτι το 1 δεν ανηκει στο π.ο. αρα δεν ειναι συνεχης στο 1,και επομενως ουτε παραγωγισιμη.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 7 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Αλεξακις]

Καλησπέρα σε όλους . Υπάρχει πιθανότητα βοήθειας για μια παράγωγο ; Γιατί γράφω αύριο και θα ήταν πολύ καλό αν κάποιος μπορούσε να με βοηθήσει σε αυτό . Ευχαριστώ .

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Lancelot]

ζηταει καπου ολη αυτην την παραγωγο ;
θα παραγωγισεις το καθενα ξεχωριστα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 6 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.