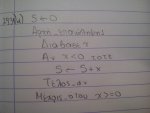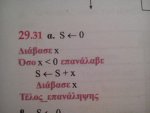ren4itoy
Νεοφερμένο μέλος


1. Να ζητείται από το χρήστη ένα ψηφίο (ακέραιος αριθμός από το 0 μέχρι το 9) και τρεις ακέραιοι αριθμοί από το 0 ως το 999.999. Ο αλγόριθμος να κάνει έλεγχο τιμών που δίνει ο χρήστης και αν ειναι δεκαδικοί ή/και πέραν των ορίων να του εμφανίζει σχετικό μήνυμα (άλλο για δεκαδική τιμή και άλλο για τιμή πέραν των ορίων) και να τον καλεί να καταχωρίσει ξανά σωστή τιμή. Έπειτα ο αλγόριθμος να βρίσει πόσες εμφανίσεις έχει το ψηφίο που έδωσε ο χρήστης συνολικά στους τρεις ακέραιους αριθμούς. ΠΡΟΣΟΧΗ: Αν ο χρήστης δώσει τον αριθμό 124, δε θεωρείται ότι ειναι ο αριθμός 000124 και συνεπώς έχει 3 εμφανίσεις του ψηφίου 0.
2. Να ζητείται από το χρήστη ένα γράμμα και πέντε λέξεις. ΟΙ λέξεις να δίνονται γράμμα-γράμμα και να θεωρείται ότι τελείωσε η λέξη όταν ο χρήστης πληκτρολογήσει το χαρακτήρα <<*>> . Ο αλγόριθμος να βρίσκει σε πόσες λέξεις βρέθηκε το γράμμα αυτό και από πόσες φορές στην κάθε μία. Θεωρείται ότι μια λέξη μπορεί να έχει το πολύ 172 γράμματα.
3. Να ζητούνται από το χρήστη 20 αριθμοί και στη συνέχεια ο αλγόριθμος να τους εμφανίζει κατά αύξουσα σειρά. Στη συνέχεια να εμφανίζεται πόσοι από τους 20 αριθμούς ήταν ακέραιοι και πόσοι θετικοί, πόσοι μηδέν και πόσοι αρνητικοί. Ο χρήστης μπορεί να δώσει τον ίδιο αριθμό και πάνω από μια φορά
ΠΑΡΑΚΑΛΩ ΑΓΝΟΗΣΤΕ ΟΤΙ ΛΕΕΙ ΑΛΓΟΡΙΘΜΟΣ! Μας είπε ότι το θέλει σαν πρόγραμμα στη ΓΛΩΣΣΑ.
Όποιος μπορεί να βοηθήσει θα το εκτιμήσω ιδιαίτερα! Ευχαριστώ!
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
frofru
Εκκολαπτόμενο μέλος


Η άσκηση ειναι η εξής: Να αναπτύξετε αλγόριθμο που θα διαβάζει έναν ακέραιο Ν>0 και θα υπολογίζει το άθροισμα S = 5/3 + 25/9 + 125/27 + ... μέχρι το S να ξεπεράσει την τιμή του ακέραιου Ν. Στο τέλος ο αλγόριθμος θα πρέπει να εκτυπώνει το πλήθος των όρων του αθροίσματος.
Λύση:
Αλγόριθμος άσκηση
α <- 5
β <- 3
S <- 0
μ <- 0
Όσο S <= N επανάλαβε
S <- S + α / β
α <- α * 5
β <- β*3
μ <- μ+1
Τέλος_επανάληψης
Εκτύπωσε S,μ
Τέλος άσκηση
Ευχαριστω! :-)
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Vold
Πολύ δραστήριο μέλος


Καλησπέρα, έλυσα μια άσκηση πάνω στην όσο...επανάλαβε και θα ήθελα, αν μπορείτε, να ελέγξετε αν η λύση μου είναι σωστή.
Η άσκηση ειναι η εξής: Να αναπτύξετε αλγόριθμο που θα διαβάζει έναν ακέραιο Ν>0 και θα υπολογίζει το άθροισμα S = 5/3 + 25/9 + 125/27 + ... μέχρι το S να ξεπεράσει την τιμή του ακέραιου Ν. Στο τέλος ο αλγόριθμος θα πρέπει να εκτυπώνει το πλήθος των όρων του αθροίσματος.
Λύση:
Αλγόριθμος άσκηση
α <- 5
β <- 3
S <- 0
μ <- 0
Όσο S <= N επανάλαβε
S <- S + α / β
α <- α * 5
β <- β*3
μ <- μ+1
Τέλος_επανάληψης
Εκτύπωσε S,μ
Τέλος άσκηση
Ευχαριστω! :-)
Ναι, είναι οκ.
Γενικά δεν έχει κάποια ιδιαίτερη δυσκολία....
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
PiDefiner
Δραστήριο μέλος


Καλησπέρα, έλυσα μια άσκηση πάνω στην όσο...επανάλαβε και θα ήθελα, αν μπορείτε, να ελέγξετε αν η λύση μου είναι σωστή.
Η άσκηση ειναι η εξής: Να αναπτύξετε αλγόριθμο που θα διαβάζει έναν ακέραιο Ν>0 και θα υπολογίζει το άθροισμα S = 5/3 + 25/9 + 125/27 + ... μέχρι το S να ξεπεράσει την τιμή του ακέραιου Ν. Στο τέλος ο αλγόριθμος θα πρέπει να εκτυπώνει το πλήθος των όρων του αθροίσματος.
Η επανάληψη είναι σωστή, αλλά δεν διαβάζεις πουθενά τον Ν. Θα πρέπει να τον διαβάσεις μέσα σε μέχρις_ότου για να κάνεις έλεγχο εγκυρότητας.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
frofru
Εκκολαπτόμενο μέλος


Ναι, είναι οκ.
Γενικά δεν έχει κάποια ιδιαίτερη δυσκολία....
Ναι, εχεις απολυτο δικιο ξεχασα να γραψω το διαβασε Ν.Η επανάληψη είναι σωστή, αλλά δεν διαβάζεις πουθενά τον Ν. Θα πρέπει να τον διαβάσεις μέσα σε μέχρις_ότου για να κάνεις έλεγχο εγκυρότητας.
Σας ευχαριστω πολυ για τις αμεσες απαντησεις!
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Valous
Εκκολαπτόμενο μέλος


Καλησπέρα, έλυσα μια άσκηση πάνω στην όσο...επανάλαβε και θα ήθελα, αν μπορείτε, να ελέγξετε αν η λύση μου είναι σωστή.
Η άσκηση ειναι η εξής: Να αναπτύξετε αλγόριθμο που θα διαβάζει έναν ακέραιο Ν>0 και θα υπολογίζει το άθροισμα S = 5/3 + 25/9 + 125/27 + ... μέχρι το S να ξεπεράσει την τιμή του ακέραιου Ν. Στο τέλος ο αλγόριθμος θα πρέπει να εκτυπώνει το πλήθος των όρων του αθροίσματος.
Λύση:
Αλγόριθμος άσκηση
α <- 5
β <- 3
S <- 0
μ <- 0
Όσο S <= N επανάλαβε
S <- S + α / β
α <- α * 5
β <- β*3
μ <- μ+1
Τέλος_επανάληψης
Εκτύπωσε S,μ
Τέλος άσκηση
Ευχαριστω! :-)
Μπορεις να δεις και τους αριθμους ως δυναμεις. Αφου 5-25-125 ειναι δυναμεις του 5^ν
και 3-9-27 ειναι δυναμεις του 3^ν..
Just sayin' εναν ακομα τροπο σκεψης.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
PiDefiner
Δραστήριο μέλος


Και μια δική μου ερώτηση: Στο πρόγραμμα μπορώ να χρησιμοποιώ κανονικά τις έτοιμες συναρτήσεις των αλγορίθμων, έτσι;
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ren4itoy
Νεοφερμένο μέλος


Για την τελευταία πρόταση: λογικά αυτό θέλει να πει απλά όπως καταλαβαίνεις οι διατυπώσεις είναι λίγο προβληματικές...
Ευχαριστώ πολύ που κάθεσαι να ασχοληθείς!
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
PiDefiner
Δραστήριο μέλος


Λύνεται και χωρίς πίνακες, αλλά βγαίνει τεράστιος.
Ορίστε και μερικά κομμάτια για να σε βοηθήσουν, αν δεν ξέρεις τι να κάνεις. Μη δίνεις σημασία στο ονόματα των μεταβλητών, ξεκίνησα να το λύνω χωρίς πίνακες.
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ΑΝ ψ1<>Α_Μ(ψ1) ΤΟΤΕ
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΔΕΚΑΔΙΚΟ. ΔΩΣΕ ΕΝΑΝ ΑΚΕΡΑΙΟ'
ΔΙΑΒΑΣΕ ψ1
ΑΛΛΙΩΣ_ΑΝ ψ1<0 Ή ψ1>9
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΤΙΜΗ ΕΚΤΟΣ ΟΡΙΩΝ. ΔΩΣΕ ΑΡΙΘΜΟ ΑΠΟ ΤΟ 0 ΜΕΧΡΙ ΤΟ 9'
ΔΙΑΒΑΣΕ ψ1
ΤΕΛΟΣ_ΑΝ
ΜΕΧΡΙΣ_ΌΤΟΥ ψ1=Α_Μ(ψ1) ΚΑΙ ψ1>=0 ΚΑΙ ψ1<=9
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ΑΝ τ1<>Α_Μ(τ1) ΤΟΤΕ
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΔΕΚΑΔΙΚΟ. ΔΩΣΕ ΕΝΑΝ ΑΚΕΡΑΙΟ'
ΔΙΑΒΑΣΕ τ1
ΑΛΛΙΩΣ_ΑΝ τ1<0 Ή τ1>999999
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΤΙΜΗ ΕΚΤΟΣ ΟΡΙΩΝ. ΔΩΣΕ ΑΡΙΘΜΟ ΑΠΟ ΤΟ 0 ΜΕΧΡΙ ΤΟ 999999'
ΔΙΑΒΑΣΕ τ1
ΤΕΛΟΣ_ΑΝ
ΜΕΧΡΙΣ_ΌΤΟΥ τ1=Α_Μ(τ1) ΚΑΙ τ1>=0 ΚΑΙ τ1<=999999
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ΑΝ τ2<>Α_Μ(τ2) ΤΟΤΕ
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΔΕΚΑΔΙΚΟ. ΔΩΣΕ ΕΝΑΝ ΑΚΕΡΑΙΟ'
ΔΙΑΒΑΣΕ τ2
ΑΛΛΙΩΣ_ΑΝ τ2<0 Ή τ2>999999
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΤΙΜΗ ΕΚΤΟΣ ΟΡΙΩΝ. ΔΩΣΕ ΑΡΙΘΜΟ ΑΠΟ ΤΟ 0 ΜΕΧΡΙ ΤΟ 999999'
ΔΙΑΒΑΣΕ τ2
ΤΕΛΟΣ_ΑΝ
ΜΕΧΡΙΣ_ΌΤΟΥ τ2=Α_Μ(τ2) ΚΑΙ τ2>=0 ΚΑΙ τ2<=999999
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ΑΝ τ3<>Α_Μ(τ3) ΤΟΤΕ
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΔΕΚΑΔΙΚΟ. ΔΩΣΕ ΕΝΑΝ ΑΚΕΡΑΙΟ'
ΔΙΑΒΑΣΕ τ3
ΑΛΛΙΩΣ_ΑΝ τ3<0 Ή τ3>999999
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΤΙΜΗ ΕΚΤΟΣ ΟΡΙΩΝ. ΔΩΣΕ ΑΡΙΘΜΟ ΑΠΟ ΤΟ 0 ΜΕΧΡΙ ΤΟ 999999'
ΔΙΑΒΑΣΕ τ3
ΤΕΛΟΣ_ΑΝ
ΜΕΧΡΙΣ_ΌΤΟΥ τ3=Α_Μ(τ3) ΚΑΙ τ3>=0 ΚΑΙ τ3<=999999
ντ1←ψ1
ψηφ1←0
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ψηφ1←ψηφ1+1
ντ1←ντ1 div 10
ΜΕΧΡΙΣ_ΟΤΟΥ ντ1=0
ντ2←τ2
ψηφ2←0
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ψηφ2←ψηφ2+1
ντ2←ντ2 div 10
ΜΕΧΡΙΣ_ΟΤΟΥ ντ2=0
ντ3←τ3
ψηφ3←0
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ψηφ3←ψηφ3+1
ντ3←ντ3 div 10
ΜΕΧΡΙΣ_ΟΤΟΥ ντ3=0
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ren4itoy
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
PiDefiner
Δραστήριο μέλος


 Απλώς αυτά που είχα να κάνω τελικά μου πήραν παραπάνω απ' ότι υπολόγιζα και δεν πρόλαβα να ασχοληθώ.
Απλώς αυτά που είχα να κάνω τελικά μου πήραν παραπάνω απ' ότι υπολόγιζα και δεν πρόλαβα να ασχοληθώ.Πάλι, δεν έφτασα μέχρι το τέλος, αλλά την έχω σαφώς σημαζέψει.
Θα ήθελα, αν μπορεί κάποιος να μου επικυρώσει 2 πράγματα, για να συνεχίσω την άσκσηση.
1) Η χρήση της έτοιμης συνάρτησης Α_Μ(x) μπορεί να γίνει κανονικά σε πρόγραμμα;
2) Αυτό που κάνω στο τέλος είναι αποδεκτό; Δηλαδή η δημιουργία δισδιάστατου πίνακα με διαφορετικό αριθμό στηλών (αφού δεν γνωρίζω πόσα ψηφία έχει κάθε αριθμός που διάβασα);
ΔΙΑΒΑΣΕ Ψ
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ΑΝ Ψ<>Α_Μ(Ψ) ΤΟΤΕ
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΜΗ ΑΚΕΡΑΙΟ'
ΔΙΑΒΑΣΕ Ψ
ΑΛΛΙΩΣ_ΑΝ Ψ<0 Ή Ψ>9 ΤΟΤΕ
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΑΡΙΘΜΟ ΕΚΤΟΣ ΟΡΙΩΝ'
ΔΙΑΒΑΣΕ Ψ
ΤΕΛΟΣ_ΑΝ
ΜΕΧΡΙΣ_ΟΤΟΥ Ψ=Α_Μ(Ψ) ΚΑΙ Ψ>=0 ΚΑΙ Ψ<=9
ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 3
ΔΙΑΒΑΣΕ Τ[i]
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
ΑΝ Τ[i]<>Α_Μ(Τ[i]) ΤΟΤΕ
ΓΡΑΨΕ 'ΕΔΩΣΕΣ ΜΗ ΑΚΕΡΑΙΟ'
ΔΙΑΒΑΣΕ T[i]
ΑΛΛΙΩΣ_ΑΝ Τ[i]<0 Ή Τ[i]>999999 ΤΟΤΕ
ΓΡΑΨΕ 'ΈΔΩΣΕΣ ΑΡΙΘΜΟ ΕΚΤΟΣ ΟΡΙΩΝ'
ΔΙΑΒΑΣΕ Τ[i]
ΤΕΛΟΣ_ΑΝ
ΜΕΧΡΙΣ_ΟΤΟΥ Τ[i]=Α_Μ(Τ[i]) ΚΑΙ Τ[i]>=0 ΚΑΙ T[i]<=999999
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 3
ντ←Τ[i]
Α[i]←0
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ
Α[i]←Α[i] + 1
ντ←ντ mod 10
ΜΕΧΡΙΣ_ΟΤΟΥ ντ=0
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
!Τώρα έχεις σε κάθε στοιχείο του πίανακα Α τον αριθμό των ψηφίων καθενός από τους 3 αριθμούς
ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 3
ΓΙΑ j ΑΠΟ 1 ΜΕΧΡΙ Α[i]
Ψ[i,j]← Τ[i] mod 10
Τ[i]← Τ[i] div 10
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
!Στην παραπάνω επανάληψη δημιουργούμε έναν δισδιάστατο πίνακα. Σε κάθε γραμμή του, υπάρχουν τα ψηφία του 3ψήφιου αριθμού που διαβάσαμε, ένα σε κάθε στήλη.Edit1: μέχρι να απαντήσει κάποιος, δίαβασε την άσκηση μέχρι εδώ και πες μου αν δεν κατάλαβες κάτι ή αν εντοπίσεις κάποιο λάθος.
Edit2: Τελείωσα την 2η. Πιθανολογώ (όπως είπα, δεν είναι και αρκετά σαφείς οι εκφωνήσεις), πως μπορεί να θέλουν πίνακα, αφού δίνει τον περιορισμό των 172 γραμμάτων ανά λέξη, αλλά εφ' όσον ζητά "να τις βρίσκει", δεν είναι λάθος έτσι όπως το έκανα. Αν θες, μπορώ να στο γράψω και με πίνακα.
ΔΙΑΒΑΣΕ Γ !ΔΙΑΒΑΖΩ ΓΡΑΜΜΑ
P←0
ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 5 !ΘΑ ΔΙΑΒΑΣΕΙ 5 ΛΕΞΕΙΣ
ΠΛ←0
ΑΡΧΗ_ΕΠΑΝΑΛΗΨΗΣ !ΔΙΑΒΑΖΩ ΓΡΑΜΜΑΤΑ ΜΕΧΡΙ ΝΑ ΤΕΛΕΙΩΣΕΙ Η ΛΕΞΗ
ΔΙΑΒΑΣΕ ΓΡ
ΑΝ ΓΡ=Γ ΤΟΤΕ !ΕΛΕΓΧΟΣ ΑΝ ΤΟ ΓΡΑΜΜΑ ΤΗΣ ΛΕΞΗΣ ΕΙΝΑΙ ΙΔΙΟ ΜΕ ΤΟ ΓΡΑΜΑ ΠΟΥ ΔΙΑΒΑΣΕ ΑΡΧΙΚΑ
ΠΛ←ΠΛ+1 !ΑΝ ΕΙΝΑΙ, ΑΥΞΑΝΩ ΤΟ ΠΛΗΘΟΣ (ΠΛΗΘΟΣ ΓΙΑ ΚΑΘΕ ΛΕΞΗ)
ΤΕΛΟΣ_ΑΝ
ΜΕΧΡΙΣ_ΌΤΟΥ ΓΡ='*'
ΓΡΑΨΕ ΠΛ !ΕΜΦΑΝΙΖΩ ΤΟ ΠΛΗΘΟΣ ΠΟΥ ΕΝΤΟΠΙΣΤΗΚΕ ΤΟ ΓΡΑΜΜΑ ΣΤΗ ΛΕΞΗ
ΑΝ ΠΛ<>0 ΤΟΤΕ !ΑΝ ΕΧΕΙ ΒΡΕΘΕΙ ΕΣΤΩ ΚΑΙ ΜΙΑ ΦΟΡΑ ΤΟ ΓΡΑΜΜΑ ΣΤΗ ΛΕΞΗ
P←P+1 !ΑΥΞΑΝΩ ΤΟ ΠΛΗΘΟΣ
ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΡΑΨΕ P !ΕΜΦΑΝΙΖΩ ΣΕ ΠΟΣΕΣ ΑΠΟ ΤΙΣ 5 ΛΕΞΕΙΣ ΕΜΦΑΝΙΣΤΗΚΕ ΤΟ ΓΡΑΜΜΑEdit3: Έτοιμη και η 3η άσκηση. Τώρα μένει να δουλέψω την 1η μέχρι το τέλος, αλλά για την ώρα δεν προλαβαίνω. Αν εντοπίσει κάποιος κάποιο λάθος ας μου πει.
ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 20
ΔΙΑΒΑΣΕ Τ[i] !ΔΙΑΒΑΖΩ ΤΟΥΣ 20 ΑΡΙΘΜΟΥΣ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΙΑ i ΑΠΌ 2 ΜΈΧΡΙ 20 !ΤΟΥΣ ΤΑΞΙΝΟΜΩ
ΓΙΑ j ΑΠΌ 20 ΜΕΧΡΙ i ΜΕ_ΒΉΜΑ -1
ΑΝ Τ[j-1]>T[j] TOTE !ΚΑΤΑ ΑΥΞΟΥΣΑ ΣΕΙΡΑ
temp←Τ[j-1]
Τ[j-1]←Τ[j]
Τ[j]←temp
ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΙΑ i ΑΠΟ 1 ΜΕΧΡΙ 20 !ΤΟΥΣ ΕΜΦΑΝΙΖΩ ΤΑΞΙΝΟΜΗΜΕΝΟΥΣ
ΓΡΑΨΕ Τ[i]
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Θ←0 !ΠΛΗΘΟΣ ΘΕΤΙΚΩΝ
Μ←0 !ΠΛΗΘΟΣ ΜΗΔΕΝΙΚΩΝ
Α←0 !ΠΛΗΘΟΣ ΑΚΕΡΑΙΩΝ
ΓΙΑ i ΑΠΟ 1 ΜΈΧΡΙ 20
ΑΝ Α_Μ(Τ[i])=Τ[i] ΤΟΤΕ
Α←Α+1
ΤΕΛΟΣ_ΑΝ !ΈΝΑΣ ΑΚΕΡΑΙΟΣ ΜΠΟΡΕΊ ΝΑ ΕΊΝΑΙ ΘΕΤΙΚΌΣ Ή ΑΡΝΗΤΙΚΌΣ, ΟΠΌΤΕ ΜΠΑΊΝΕΙ ΣΕ ΞΕΧΩΡΙΣΤΌ ΑΝ
ΑΝ Τ[i]>0 ΤΟΤΕ !ΑΝ ΕΙΝΑΙ ΘΕΤΙΚΟΣ
Θ←Θ+1
ΑΛΛΙΩΣ_ΑΝ Τ[i]=0 ΤΟΤΕ !ΑΝ ΔΕΝ ΕΙΝΑΙ ΘΕΤΙΚΟΣ, ΑΛΛΑ ΕΙΝΑΙ ΜΗΔΕΝ
Μ←Μ+1
ΤΕΛΟΣ_ΑΝ
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΓΡΑΨΕ Α, Θ, Μ, 20-(Θ+Μ) !ΤΟ ΑΠΟΤΕΛΕΣΜΑ ΤΗΣ ΠΡΑΞΗΣ 20-(Θ+Μ) ΜΟΥ ΔΙΝΕΙ ΤΟ ΠΛΗΘΟΣ ΤΩΝ ΑΡΝΗΤΙΚΩΝ. Θ+Μ ΕΙΝΑΙ ΤΟ ΠΛΗΘΟΣ ΤΩΝ ΜΗ ΑΡΝΗΤΙΚΩΝ ΑΡΙΘΜΩΝ.Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Vold
Πολύ δραστήριο μέλος


Το δεύτερο δεν ισχύει, σε καμία περίπτωση. Όπως και στις κανονικές γλώσσες προγραμματισμού, έτσι και στην "ψευδογλώσσα" οι πίνακες είναι πάντα ορθ. παραλ.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
PiDefiner
Δραστήριο μέλος


Το πρώτο απ' ότι θυμάμαι ισχύει. Σίγουρα ισχύει σε αλγορίθμους, οπότε λογικό είναι νομίζω να ισχύει και για προγράμματα
Το δεύτερο δεν ισχύει, σε καμία περίπτωση. Όπως και στις κανονικές γλώσσες προγραμματισμού, έτσι και στην "ψευδογλώσσα" οι πίνακες είναι πάντα ορθ. παραλ.
Κρίμα... τώρα θα πρέπει να το κάνω τρεις φορές.

Edit: Και άλλη ερώτηση. Η έκφραση 3.0 = 3 είναι αληθής;
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eyb0ss
Δραστήριο μέλος


Άρα για να βρούμε ακέραιο μέρος σε αλγόριθμο:
Διάβασε x
Αν x>0 και x<1 τότε
intx <-- 0
Τελος_αν
Αν x>=1 τότε
i <-- 1
Όσο x-i>=1 ή x-i<0 επανάλαβε
i <-- i+1
Τέλος_επανάληψης
intx <-- i
Τελος_αν
Αν x<=0 και x>-1 τότε
intx <-- -1
Τελος_αν
Αν x<=-1 τότε
i <-- -1
Όσο x-i>=1 ή x-i<0 επανάλαβε
i <-- i-1
Τέλος_επανάληψης
intx <-- i
Τελος_αν
To intx είναι το ακέραιο μέρος του x.
Συγνώμη για τυχόν συντακτικά λάθη.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Vold
Πολύ δραστήριο μέλος


Edit: Και άλλη ερώτηση. Η έκφραση 3.0 = 3 είναι αληθής;
Προφανώς κι όχι. Όταν μιλάμε για προγραμματισμό, ένας δεκαδικός αριθμός δεν είναι ίσος με έναν ακέραιο.
Δεκαδικός είναι ο αριθμός που έχει κινητή υποδιαστολή, δεν σημαίνει απαραίτητα πως πρέπει να είναι και διάφορο του μηδενός, το δεκαδικό μέρος.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
PiDefiner
Δραστήριο μέλος


Προφανώς κι όχι. Όταν μιλάμε για προγραμματισμό, ένας δεκαδικός αριθμός δεν είναι ίσος με έναν ακέραιο.
Δεκαδικός είναι ο αριθμός που έχει κινητή υποδιαστολή, δεν σημαίνει απαραίτητα πως πρέπει να είναι και διάφορο του μηδενός, το δεκαδικό μέρος.
Είσαι σίγουρος;

Γιατί, πρώτον, ό,τι έχω γράψει μέχρι τώρα, είναι λάθος αν δεν ισχύει αυτό, και δεύτερον, ο Online διευρμηνευτής της γλώσσας το βγάζει αληθές (τώρα κατεβάζω και την Γλωσσομάθεια, να το δοκιμάσω εκεί).

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


3 == 3.0 θα γίνει implicit cast σε float και θα επιστρέψει true.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Vold
Πολύ δραστήριο μέλος


Απλά ο δεκαδικός(ή αντίστροφα, ανάλογα) μετατρέπεται στον άλλο και τον δέχεται ως σωστό.
Οπότε ναι, 3 == 3.0.

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
PiDefiner
Δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
frofru
Εκκολαπτόμενο μέλος


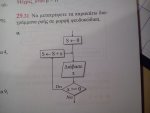
 Εχω μια ασκηση πανω στα διαγραμματα ροης στην δομη επαναληψης και θα ηθελα να μου πειτε αν η λυση μου ειναι σωστη, καθως το βοηθημα δινει λυση με διαφορετικη δομη επαναληψης. Ευχαριστω!
Εχω μια ασκηση πανω στα διαγραμματα ροης στην δομη επαναληψης και θα ηθελα να μου πειτε αν η λυση μου ειναι σωστη, καθως το βοηθημα δινει λυση με διαφορετικη δομη επαναληψης. Ευχαριστω! Η ασκηση: Η λυση : Η λυση του βοηθηματος :
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 64 μέλη διάβασαν αυτό το θέμα:
- marios_ar
- vade
- tomftw
- john_55
- akis_95
- Marios2020
- Hased Babis
- Mara2004
- Mary06
- Valous
- Ilovemycats27
- katia.m
- Anna_kitty
- antonis97
- gewrgioyp
- Panagiotis849
- Σωτηρία
- marian
- ggl
- tsiobieman
- elenicar
- Scandal
- Δήμος56103
- eukleidhs1821
- calliope
- kwstaseL
- Eri0611
- liaiscool
- leo41
- Georgekk
- Athens2002
- Johnman97
- imkindalost
- panagiotis G
- Giovanni5
- marsenis
- thecrazycretan
- the purge
- eri548
- Ria99
- JohnGreek
- lostpfg
- Vold
- Λαμπρινηη
- SlimShady
- tasost
- Vasilina93
- kvstas92
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki