DumeNuke
Τιμώμενο Μέλος


Ξεκινάμε με μια υπόθεση....για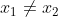
άρα,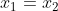
διαφορετικά x (ίσα μεταξύ τους)
Δεν κατάλαβα πώς συνδέεις τη μέθοδο της Αντιθετοαντιστροφής με τη διαφορετικότητα των x1 και x2.
Πώς, δηλαδή, γίνεται δύο μεταβλήτες να είναι ίσες και διαφορετικές μεταξύ τους, ταυτόχρονα?

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nPb
Επιφανές μέλος


....για
προσπαθώντας να δείξω τη σκέψη ότι οι τιμές δυο ανεξάρτητων μεταβλητών είναι ίσες τότε και μόνο αν οι ανεξάρτητες μεταβλητές είναι ίσες (από αλγεβρική άποψη) εφόσον σε κάθε ανεξάρτητη μεταβλητή αντιστοιχεί μοναδική τιμή (εξαρτημένη μεταβλητή). Οπότε για να είναι ίσες αυτές οι τιμές υπό την ίδια συνάρτηση πάντα προϋποθέτουν ίδια είσοδο (input): ίδια ανεξάρτητη μεταβλητή x.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
petrosbomb
Νεοφερμένο μέλος


g "1-1",και για κάθε χ>0 ισχύει
x^2 f(f(x))=f^3 (x)
και g(x)=x^2 f(x)
Να βρεθούν η g και η f
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Silent_Killer
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
gersi
Εκκολαπτόμενο μέλος


Δίνονται οι μιγαδικοί:
α)την τιμη του x,
β) τον μιγαδικό
Εδω ειναι μια προσπαθεια μου αλλα καπου τα κανω θαλασσα.Μπορεί κάποιος να γράψει την λυση αναλυτικά;
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Peace_
Τιμώμενο Μέλος


Kαι επίσης... Τα άκρα ολοκλήρωσης μπορεί να αλλάξουν αν βγάλεις ένα (-) έξω από το ολοκλήρωμα;
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
gersi
Εκκολαπτόμενο μέλος


Πότε μία εξίσωση έχει τριπλές ρίζες;
Kαι επίσης... Τα άκρα ολοκλήρωσης μπορεί να αλλάξουν αν βγάλεις ένα (-) έξω από το ολοκλήρωμα;
- Μια εξισωση εχει 3 ριζες οταν ειναι τουλαχιστον 3ου βαθμου ή μεγαλυτερη, π.χ.
- Λεω τουλαχιστον 3ου βαθμου ή μεγαλυτερη, διοτι μια εξισωση 4ου βαθμου εαν την παραγοντοποιησεις μπορει να εχει μια διπλη ριζα (διακρινουσα Δ=0) και δυο ριζες Χ1,Χ2.
- Στο ολοκληρωμα
βαζοντας ενα (-) εξω απο το ολοκληρωμα τα ακρα αντιστρεφονται, δηλαδη
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
millie_M
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
millie_M
Νεοφερμένο μέλος


(x+ - λ)*(x+ - λ)*(x+ - λ)*...........όταν θα γίνει αυτό και θα έχεις ένα σκασμό από γινόμενα τότε αφού λ εR τότε είναι σαν να λειτουργείς με αριθμούς . Βάλε έναν αριθμό στη θέση του λ και κάνε ότι θα έκανες με μία τέτοια παράσταση....
ΠΟΥ είμαι εγώ σπαστικιά!!! αααα άκου κάτι μικρούλια και απαίδευτα
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DumeNuke
Τιμώμενο Μέλος


Για να είναι τα πολυώνυμα ίσα θα πρέπει τα πεδία ορισμού τους να είναι ίσα (AP=AQ) και, επίσης, P(x)=Q(x), για κάθε χ που ανήκει στο πεδίο ορισμού.
Δηλαδή α=δ και β=ε και γ=ζ. Το δίκο σου σύστημα, λογικά, θα δίνει ανάλογες σχέσεις με λ. Λύνεις το σύστημα και βρίσκεις τις δυνατές τιμές του λ.
Επίσης, στην δοθείσα μορφή, οι συναρτήσεις έχουν λάθος. Πρέπει να προσθέσεις κάπου παρενθέσεις. Η f(x) έχει ως μεγιστοβάθμιο το χ^2, ενώ η g(x) το χ^3, επομένως δεν γίνεται να είναι ίσες.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
gersi
Εκκολαπτόμενο μέλος


Να αποδειξετε οτι:
Η Λύση μου είναι:
Αρα
Ετσι μπορω να το αποδειξω ή πρεπει να ξέρω και την μονοτονία της f;
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
notis_19
Πολύ δραστήριο μέλος


Αυτά νομίζω εγώ..
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


Έστω συνάρτηση f:[a,b]R η οποια ειναι συνεχης και τετοια ωστε: f(a+b-x)=f(x) για καθε x
[a,b]
Να αποδειξετε οτι:
Η Λύση μου είναι:
Αρα
Ετσι μπορω να το αποδειξω ή πρεπει να ξέρω και την μονοτονία της f;
Υπολογισε το ολ απο α στο β xf(x) και οπου f(x) βαλε f(a+b-x),δηλαδη υπολογισε το ολοκληρημα απο α στο β x*f(a+b-x) ,κανε αλλαγη μεταβλητης και εχε τα ματια σου 14 μετα ,αν εχεισ προβλημα γραψε και θα δωσω την λυση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
gersi
Εκκολαπτόμενο μέλος


Ολα ενταξει μετα απο λιγο (25 λεπτα) καψιμο το εβγαλα.Υπολογισε το ολ απο α στο β xf(x) και οπου f(x) βαλε f(a+b-x),δηλαδη υπολογισε το ολοκληρημα απο α στο β x*f(a+b-x) ,κανε αλλαγη μεταβλητης και εχε τα ματια σου 14 μετα ,αν εχεισ προβλημα γραψε και θα δωσω την λυση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
georgekok
Νεοφερμένο μέλος



δινονται δυο συναρτησεις f,g : [ α,β] -> R . αν g(x) >0 για καθε χ που ανηκει στο [α,β] να δειξετε οτι υπαρχει ενα τουλαχιστον ξ που ανηκει στο [ α,β] τετοιο ωστε :
∫f(x)g(x)dx = f(ξ) * ∫g(x) dx .(ακρα ολοκληρωσης α,β)
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


μια βοηθεια
δινονται δυο συναρτησεις f,g : [ α,β] -> R . αν g(x) >0 για καθε χ που ανηκει στο [α,β] να δειξετε οτι υπαρχει ενα τουλαχιστον ξ που ανηκει στο [ α,β] τετοιο ωστε :
∫f(x)g(x)dx = f(ξ) * ∫g(x) dx .(ακρα ολοκληρωσης α,β)
Εγραψες σιγουρα σωστα την εκφωνηση?Για ξανα check.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 8 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

