Γιάννης123
Εκκολαπτόμενο μέλος


πρωτα θα παρει τις δυο πρωτες σχεσει για τα μετρα θα τις υψωσει στο τετραφωνο και θα λυσεις ως προς τους συζηγεις και θα τους αντικαταστησεις σε αυτο που θα εχεις βγαλει
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dimidimi
Νεοφερμένο μέλος


δεν θα κανεις απαλοιφη, για να αποδειξεις οτι ειναι πραγματικος θα το κανεις με την κλασσικη διαδικασια (w=w(συζηγης))
πρωτα θα παρει τις δυο πρωτες σχεσει για τα μετρα θα τις υψωσει στο τετραφωνο και θα λυσεις ως προς τους συζηγεις και θα τους αντικαταστησεις σε αυτο που θα εχεις βγαλει
Αυτό που λες το έχω κάνει! Το μετά είναι το πρόβλημα..πως θα συνεχίσω? Τα "ν" πως θα φύγουν από τους εκθέτες?
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Γιατί να φύγουν; Εσύ θες να αποδείξεις ότι :Αυτό που λες το έχω κάνει! Το μετά είναι το πρόβλημα..πως θα συνεχίσω? Τα "ν" πως θα φύγουν από τους εκθέτες?
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Γιάννης123
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dimidimi
Νεοφερμένο μέλος


Γιατί να φύγουν; Εσύ θες να αποδείξεις ότι :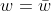
σωστά!!!! thanks

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dimidimi
Νεοφερμένο μέλος


Εγώ σκέφτηκα πως αρχικά λέμε: Έστω ότι z1/z2 e R! και μετά ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dimidimi
Νεοφερμένο μέλος


Παιδιά κάτι ακόμα! Αν z1,z2 διαφορετικές λύσεις τις εξίσωσης z*(υψωμένο στην 19)=8+9i να δειχθεί ότι z1/z2 δεν ανήκει στο R.
Εγώ σκέφτηκα πως αρχικά λέμε: Έστω ότι z1/z2 e R! και μετά ?
?
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


Παιδιά κάτι ακόμα! Αν z1,z2 διαφορετικές λύσεις τις εξίσωσης z*(υψωμένο στην 19)=8+9i να δειχθεί ότι z1/z2 δεν ανήκει στο R.
Εγώ σκέφτηκα πως αρχικά λέμε: Έστω ότι z1/z2 e R! και μετά ?

Διαίρεσα με

Επειδή


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dimidimi
Νεοφερμένο μέλος


Χωρίς να είμαι απόλυτα σίγουρος:

Διαίρεσα με
Επειδήκαταλαβαίνουμε ότι δεν ανήκει στο R
δεν ανήκει στο R
πως όμως προέκυψε ότι z1=z2 ? και επιπλέον δεν αξιοποιήσαμε ένα βασικό δεδομένο: z*=9+8i
Ευχαριστώ πολύ πάντως

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


Το αξιοποιήσαμε.πως όμως προέκυψε ότι z1=z2 ? και επιπλέον δεν αξιοποιήσαμε ένα βασικό δεδομένο: z*=9+8i
Ευχαριστώ πολύ πάντως


Αρα

Τώρα για το άλλο
Εστω



Αφου το 19 είναι περιττός θα έχουμε χ=1 άρα

το

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
aceBill
Νεοφερμένο μέλος


z1^19=z2^19 <=> (z1/z2)^19=1 <=> (z1/z2)^19=1^19 <=>* z1/z2=1 <=> z1=z2, ατοπο αφου z1 διαφορο z2
Αρα z1/z2 δεν ανηκει στο R
*Aφου υποθεσαμε οτι z1/z2 ειναι πραγματικος εχει και τις ιδιοτιτες των πραγματικων πχ α^3=1^3<=>α=1
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Έστω f:R*->R και υπάρχει αεR* ώστε:
f(x+a)=f(x)-5/f(x)-3 με f(x) διάφορο του 3
να δείξετε ότι f(x+4a)=f(x)
Παιδιά την χρειάζομαι οπωσδήποτε σήμερα άν μπορέσει κάποιος και την λύσει ας το ποστάρει εδώ αλλιώς όποτε μπορέσετε απλα σήμερα έχω τεστ και νομίζω θα βάλει κάτι τέτοιο
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Silent_Killer
Πολύ δραστήριο μέλος



ασκ.57 μπαρλας(αν το έχει κάποιος
|z-1-4i|< ή ίσο 2*(ρίζα 2 ) κ' |iw + 11 - 2i| < ή ίσο 3*ρίζα δύο
ζητάει |z-w|max κ' z=w
Το πρόβλημα μου είναι ότι δεν μπορώ να αποδείξω ότι οι κύκλοι τέμνονται διότι το μέτρο των δύο κέντρων βγαίνει ρίζα 50==> 5*(ρίζα 2) το οποίο είναι μικρότερο του 2 ρ.
Μπορεί κάποιος να με βοηθήσει στις πράξεις;
επίσης όταν έχουμε ζ*(ζ συζυγής) + 2|ζ|=3 πώς βρίσκουμε γ.τ ; παίρνουμε x + yi και υψώνουμε;
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Stavri_
Τιμώμενο Μέλος
Silent_Killer
Πολύ δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dimidimi
Νεοφερμένο μέλος


Συμείωση συντονιστή: Τα μηνύματα 6883 και 6884 προήλθαν από νήμα με παρόμοιο θέμα με το παρόν.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
aceBill
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Alexl1996
Πολύ δραστήριο μέλος


Έχουμε
Έχω ακούσει κάτι για κατάλληλες αντικαταστάσεις στο x, πάντως εγώ έχω γράψει αυτό για να το αποδείξω (λίγο θεωρητικά όμως):
Αρκεί ν.δ.ο. η f(x) δεν είναι γν.μονότονη, αφού τότε δεν θα είναι και 1-1. Έθεσα f(x)=g(x)+h(x) με g(x)=x^2004 + 1 και h(x)=-2x^2008
Όμως η g(x) είναι γν. αύξουσα για x>0 και γν.φθίνουσα για x<0 . Αντίστοιχα η h(x) είναι γν.αύξουσα για x<0 και γν.φθίνουσα για x>0. Επομένως καμία από τις 2 δεν είναι γν.μονότονη, άρα και η f(x) ως άθροισμά τους δεν θα είναι ούτε αυτή γν.μονότονη. (για αυτό δεν είμαι πολύ σίγουρος γιατί δεν μπορώ να το δείξω νομίζω). Άρα αν η f(x) δεν είναι γνησίως μονότονη, δεν θα είναι ούτε 1-1.
Μου φαίνεται σωστός ο συλλογισμός μου αλλά μάλλον παραείναι θεωρητικός...
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
IasonasM
Εκκολαπτόμενο μέλος


Για να δείξεις πως η f δεν είναι 1-1 αρκεί αν δείξεις πως υπάρχουν x1,x2 e Df με x1 διάφορο x2 ,έτσι ώστε f(x1)=f(x2).
(Γιατί αν ήταν 1-1, αφού x1 διάφορο x2 τότε f(x1) διάφορο f(x2) )
Στην συγκεκριμένη, πχ. f(1)=f(-1) (μιας και είναι άρτια)
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


εστω οτι ηταν 1-1 , εχω για x1=1 f(1)=0 , και για χ2=-1 f(-1)=0 ατοπο γιατι θα επρεπε αφου φ(χ1)=φ(χ2) => χ1=χ2 => 1=-1 που ειναι ατοπο
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 15 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

