t00nS
Εκκολαπτόμενο μέλος


Να δείξετε ότι υπάρχει μοναδικός ρε(0,5) ώστε: f(p)=3f(0)+2f(4)+15f(5)/20
Μέχρι το απόγευμα αν γίνεται..thx
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Από το θεώρημα Bolzano για την g στο (0,5) προκύπτει το ζητούμενο.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antonisd95
Δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Λύνοντας μια άσκηση χρειάστηκε να χρησιμοποιήσω ότι η F και η F^(-1) έχουν το ίδιο ίδιος μονοτονίας.Το βιβλίο δεν λέει κάτι τέτοιο, άρα φυσικά πρέπει να το αποδείξω πριν συνεχίσω; ;;
Yep.

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χαρουλιτα
Διάσημο μέλος


Θεωρω συναρτηση g(x)=f(x)-xΑν f συνεχης στο [0,3] f(0)=α και f(3)=β οπου α,β ε(0,3) να αποδειξετε οτι υπαρχει τουλαχιστον ενας αριθμος κ ε(0,3) f(κ)=κ
Η g ειναι συνεχης στο [0,3] ως διαφορα συνεχων συναρτησεων
Τοτε: g(0)=f(0)-0=f(0)=α και g(3)=f(3)-3=β-3
Eχουμε οτι β ε (0,3) δηλαδη 0<β
 => -3<β-3<0 (αφαιρω και στα δυο μελη το 3)
=> -3<β-3<0 (αφαιρω και στα δυο μελη το 3)Αρα προκυπτει οτι β-ε<0
Δηλαδη g(3)<0
Ομως α ε (0,3), αρα α>0
Επομενως g(0)g(3)<0
Απο θεωρημα Bolzano υπαρχει ενα τουλαχιστον κ ε (0,3) τετοιο ωστε g(κ)=0 => f(κ)-κ=0 => f(κ)=κ
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος


1)αν η f συνεχης στο [α,β] δειξτε οτι f(x)+1/(χ-α)+1/(χ-β)=0 εχει μια τουλαχιστον ριζα στο (α,β)
2)Αν για καθε χ ε [0,1] ισχυει 0=<f(x)=<1 δειξτε οτι η f(x) και η g(x)=x^2 εχουν ενα τουλαχιστον σημειο τομης με τετμημενη Χο ε [0,1]
3)εστω f,g συνεχεις συναρτησεις ωστε f(x)-g(x)=αx (α διαφορο του 0).Αν η f εχει δυο ετεροσημες ριζες ρι ,ρ2 δειξτε οτι η g εχει μια τουλαχιστον ριζα στο (ρ1,ρ2).
υ.γ στην 1) εκανα απαλοιφη των παρονομαστων...μετα εθεσα g(x)=f(x)(x-α)(χ-β)+(χ-β)+(χ-α)=0 .......επειτα ειπα g(α)=α-β ,g(β)=β-α ....αλλα πως θα βρω ποιο ειναι θετικο και ποιο αρνητικο.....;;;;
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antonisd95
Δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


θα ηθελα μια βοηθεια στις παρακατω ασκησεις:
1)αν η f συνεχης στο [α,β] δειξτε οτι f(x)+1/(χ-α)+1/(χ-β)=0 εχει μια τουλαχιστον ριζα στο (α,β)
2)Αν για καθε χ ε [0,1] ισχυει 0=<f(x)=<1 δειξτε οτι η f(x) και η g(x)=x^2 εχουν ενα τουλαχιστον σημειο τομης με τετμημενη Χο ε [0,1]
3)εστω f,g συνεχεις συναρτησεις ωστε f(x)-g(x)=αx (α διαφορο του 0).Αν η f εχει δυο ετεροσημες ριζες ρι ,ρ2 δειξτε οτι η g εχει μια τουλαχιστον ριζα στο (ρ1,ρ2).
υ.γ στην 1) εκανα απαλοιφη των παρονομαστων...μετα εθεσα g(x)=f(x)(x-α)(χ-β)+(χ-β)+(χ-α)=0 .......επειτα ειπα g(α)=α-β ,g(β)=β-α ....αλλα πως θα βρω ποιο ειναι θετικο και ποιο αρνητικο.....;;;;
Στο 1: Αν πολλαπλασιάσεις τα g(a) και g(b) βγαίνει -(α-β)²<0
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antonisd95
Δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


θα ηθελα μια βοηθεια στις παρακατω ασκησεις:
1)αν η f συνεχης στο [α,β] δειξτε οτι f(x)+1/(χ-α)+1/(χ-β)=0 εχει μια τουλαχιστον ριζα στο (α,β)
Θεωρούμε την συνάρτηση g(x)=f(x)(x-α)(x-β)+2x-α-β=f(x)(x-α)(x-β)+(x-α)+(x-β), x ανήκει [α,β] (προφανώς α<β)
Η g είναι συνεχής στο [α,β] αφού και η f είναι συνεχής στο [α,β]
g(α)=f(α)(α-α)(α-β)+2α-α-β=α-β<0
g(β)=f(β)(β-α)(β-β)+2β-α-β=β-α>0
Άρα g(α)g(β)<0
Επομένως σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα ξ στο (α,β) τέτοιο ώστε g(ξ)=0. Συνεπώς
g(ξ)=0 => f(ξ)(ξ-α)(ξ-β)+(ξ-α)+(ξ-β)=0 => f(ξ) +(1/(ξ-α))+(1/(ξ-β))=0
2)Αν για καθε χ ε [0,1] ισχυει 0=<f(x)=<1 δειξτε οτι η f(x) και η g(x)=x^2 εχουν ενα τουλαχιστον σημειο τομης με τετμημενη Χο ε [0,1]
Δεν δίνεται στη εκφώνηση αλλά θα θεωρήσουμε ότι η f είναι συνεχής στο [0,1].
Θεωρούμε την συνάρτηση h(x)=f(x)-g(x)=f(x)-(x^2), x ανήκει [0,1]
Η συνάρτηση h είναι συνεχής στο [0,1] αφού η f είναι συνεχής στο [0,1]
h(0)=f(0)-0^2=f(0)>=0
h(1)=f(1)-1^2=f(1)-1<=0
i) Αν f(0)=0 τότε h(0)=0 και επομένως f(0)=g(0)
ii) Αν f(1)=1 τότε h(1)=0 και επομένως f(1)=g(1)
iii) Αν h(0) διάφορο 0 και h(1) διάφορο 0 τότε h(0)>0 και h(1)<0. Επομένως h(0)h(1)<0 και επειδή η h είναι συνεχής στο [0,1] τότε σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα x0 τέτοιο ώστε h(x0)=0 => f(x0)=g(x0)
Άρα υπάρχει τουλάχιστον ένα x0 στο [0,1] τέτοιο ώστε f(x0)=g(x0)
3)εστω f,g συνεχεις συναρτησεις ωστε f(x)-g(x)=αx (α διαφορο του 0).Αν η f εχει δυο ετεροσημες ριζες ρι ,ρ2 δειξτε οτι η g εχει μια τουλαχιστον ριζα στο (ρ1,ρ2).
Χωρίς βλάβη της γενικότητας θεωρούμε ρ1<0<ρ2 έτσι ώστε f(ρ1)=f(ρ2)=0.
f(x)-g(x)=αx <=> g(x)=f(x)-αx, x ανήκει [ρ1,ρ2]
g(ρ1)=f(ρ1)-αρ1=-αρ1
g(ρ2)=f(ρ2)-αρ2=-αρ2
g(ρ1)g(ρ2)=(α^2)ρ1ρ2<0 αφού α^2>0 επειδή α διάφορο 0 και ρ1ρ2<0 αφού ρ1<0<ρ2
Η g είναι συνεχής στο [ρ1,ρ2] με g(ρ1)g(ρ2)<0. Άρα σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα ρ στο (ρ1,ρ2) τέτοιο ώστε g(ρ)=0
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


δινεται η συναρτηση
|f(x)-a|<=(x-a)²
ι) να αποδειξεται οτι η f ειναι συνεχης στο xo=α
ιι) να εξετασετε αν ειναι συνεχης στο χο=α η συναρτηση
παιδια λιγο βοηθεια σε αυτες τις ασκησεις pls
τι κανουμε σε αυτες τις ασκησεις?ξερει κανεις?
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


ενταξει με την 1 τελικα ηταν πολυ ευκολητι κανουμε σε αυτες τις ασκησεις?ξερει κανεις?
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


1) Aννα αποδειχθει οτι ειναι συνεχης στο R η
= 6xo,x=xo)
Για x, x0 ανήκουν R ισχύει:
f(x)-f(x0)=3(x^2)+5-3(x0^2)-5=3((x^2)-(x0^2))=3(x+x0)(x-X0)
Επομένως για x διάφορο x0 ισχύει:
g(x)=(f(x)-f(x0))/(x-x0)=3(x+x0)(x-x0)/(x-x0)=3(x+x0)
Άρα η g είναι συνεχής στο (-άπειρο,x0)U(x0,+άπειρο) ως πολυωνυμική
Γνωρίζουμε ότι g(x0)=6x0
lim(x->x0)g(x)=lim(x->x0)[3(x+x0)]=3(x0+x0)=3*2x0=6x0=g(x0)
Επομένως η g είναι συνεχής στο x0. Συνεπώς η g είναι συνεχής στο R.
δινεται η συναρτησητετοια ωστε για καθε χΕR να ισχυει:
|f(x)-a|<=(x-a)²
ι) να αποδειξεται οτι η f ειναι συνεχης στο xo=α
ιι) να εξετασετε αν ειναι συνεχης στο χο=α η συναρτηση
=f(a),x=a)
ι) |f(x)-a|<=(x-a)^2 <=> -(x-a)^2<=f(x)-a<=(x-a)^2 <=> a-(x-a)^2<=f(x)<=a+(x-a)^2
lim(x->a)[(x-a)^2]=(a-a)^2=0 => lim(x->a)[-(x-a)^2]=-lim[(x-a)^2]=-0=0
Επειδή lim(x->a)[-(x-a)^2]=lim(x->a)[(x-a)^2]=0 τότε σύμφωνα με το κριτήριο παρεμβολής τότε lim(x->a)(f(x)-a)=0 <=> lim(x->a)f(x)=a
Για x=a προκύπτει a-(a-a)^2<=f(a)<=a+(a-a)^2 <=> a<=f(a)<=a <=> f(a)=a
Επομένως lim(x->a)f(x)=f(a). Άρα η f είναι συνεχής στο a
ιι) -(x-a)^2<=f(x)-a<=(x-a)^2
Έχουμε:
lim(x->a)(x-a)=a-a=0 <=> lim(x->a-)(x-a)=lim(x->a+)(x-a)=0
lim(x->a)[-(x-a)]=-(a-a)=0 <=> lim(x->a-)[-(x-a)]=lim(x->a+)[-(x-a)]=0
Αν x<a τότε
x-a<=(f(x)-a)/(x-a)<=-(x-a)
lim(x->a-)(x-a)=lim(x->a-)[-(x-a)]=0 οπότε σύμφωνα με το κριτήριο παρεμβολής lim(x->a-)[(f(x)-a)/(x-a)]=0
Αν x>a τότε
-(x-a)<=(f(x)-a)/(x-a)<=x-a
lim(x->a+)[-(x-a)]=lim(x->a+)(x-a)=0 οπότε σύμφωνα με το κριτήριο παρεμβολής lim(x->a+)[(f(x)-a)/(x-a)]=0
lim(x->a-)[(f(x)-a)/(x-a)]=lim(x->a+)[(f(x)-a)/(x-a)]=0 <=> lim(x->a)[(f(x)-a)/(x-a)]=0
Άρα lim(x->a)g(x)=lim(x->a)[(f(x)-a)/(x-a)]=0. Γνωρίζουμε ότι g(a)=f(a)=a
Αν a=0 τότε g(0)=f(0)=0 και επομένως lim(x->0)g(x)=g(0) που σημαίνει ότι η g είναι συνεχής στο a=0.
Αν a διάφορο 0 τότε g(a)=a διάφορο lim(x->a)g(x)=0 που σημαίνει ότι η g δεν είναι συνεχής στο a για a διάφορο 0.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mercury
Επιφανές μέλος


Τί μπορούμε να συμπεράνουμε απο το
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


οτι αυτο μείον το συζυγή του μας κάνει μηδεν.Μία ερώτηση στα γρήγορα.
Τί μπορούμε να συμπεράνουμε απο το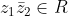
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Μία ερώτηση στα γρήγορα.
Τί μπορούμε να συμπεράνουμε απο το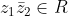
Εκτός και αν θες κάτι πιο ψαγμένο.

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
liofagos
Νεοφερμένο μέλος


f(Xo)/Χο-α=f(α)+f(β)/β-α
θετω g(x) αλλα δε μπορω να βρω τα προσημα των g(a) και g(b)
απο μπαρλα ειναι σελ 259 η 37..
βοηθεια..
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Giannis721
Νεοφερμένο μέλος


αν η f ειναι συνεχης στο [α,β] και f(a) διαφορο του μηδεν ν.δ.ο υπαρχει ενα τουλαχιστον Χο στο (α,β) τετοιο ωστε
f(Xo)/Χο-α=f(α)+f(β)/β-α
θετω g(x) αλλα δε μπορω να βρω τα προσημα των g(a) και g(b)
απο μπαρλα ειναι σελ 259 η 37..
βοηθεια..
Κάνεις απαλοιφή παρονομαστών, τα πας όλα στο πρώτο μέλος και θεωρείς συνάρτηση
Έιναι συνεχής στο [α,β] ως πράξεις συνεχών
Bolzanoulis μετά κλπ...
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mercury
Επιφανές μέλος


Αυτό που είπε ο Αντώνης βοήθησε.
Εκτός και αν θες κάτι πιο ψαγμένο.
οτι αυτο μείον το συζυγή του μας κάνει μηδεν.
Έπρεπε να αποδείξω πως ο μιγαδικός
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 3 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

