Συλλογή ασκήσεων στην Άλγεβρα

Bl4Ck_PyTh0N! · 12-08-11

Αρχική Δημοσίευση από dr.tasos:
ρε συ τι καγκουριες εκανες στην αποδειξη της (2) ενω μπορεις ευκολα να δεις οτι ${x}^{2}+{y}^{2} \geq -{xy}$
βλεπεις οτι αθροισμα θετικων = θετικο που ειναι $\geq$ αρνητικου

Αυτοσχεδίασα.Δε νομίζω ότι είναι λάθος!

Guest 018946 · 12-08-11

Αρχική Δημοσίευση από Bl4Ck_PyTh0N!:
Αυτοσχεδίασα.Δε νομίζω ότι είναι λάθος!

δεν τον πολυκαταλαβα τον τροπο σου γιαυτο

Bl4Ck_PyTh0N! · 12-08-11

Βάζω κι εγώ μια άσκηση που μου έκανε εντύπωση.

Να λύσετε την εξίσωση : (x-2)³+(x+1)³+(1-2x)³=0

akis95 · 12-08-11

παρατηρουμε οτι αν αθροισουμε τις βασεις των δυναμεων προκυπτει το μηδεν απο την euler Αν α+β+γ=0 τοτε α³+β³+γ³=3αβγ ε και μετα ολα ειναι ευκολα

Joaquín · 12-08-11

Αρχική Δημοσίευση από exc:
Ναι, η ισότητα ισχύει μόνο εφόσον ισχύει χ,y>=0.
Βέβαια, αυτό που σου λέω εγώ δεν έχει καμία σχέση με αυτό που έκανες. Κοίτα:
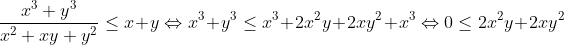
$\frac{x^3+y^3}{x^2+xy+y^2}\leq x+y\Leftrightarrow x^3+y^3\leq x^3+2x^2y+2xy^2+x^3\Leftrightarrow 0\leq 2x^2y+2xy^2$
το οποίο (τελευταίο) ισχύει για χ,y>=0.

Από που κι ως που να κάνεις χιαστί στην ανισότητα?

antwwwnis · 12-08-11

Αρχική Δημοσίευση από Alchemist:
Από που κι ως που να κάνεις χιαστί στην ανισότητα?

Δεν υπάρχει χιαστί, αλλά πολλαπλασιασμός κατα μέλη με μη αρνητική ποσότητα.
(από εκφώνηση χ y >0 )

Bl4Ck_PyTh0N! · 12-08-11

Αρχική Δημοσίευση από akis15:
παρατηρουμε οτι αν αθροισουμε τις βασεις των δυναμεων προκυπτει το μηδεν απο την euler Αν α+β+γ=0 τοτε α³+β³+γ³=3αβγ ε και μετα ολα ειναι ευκολα

Πολύ καλά!Αυτή τη λύση περίμενα!

Όποιος δεν κατάλαβε τη λύση του φίλου μας Άκη μπορεί να μου ζητήσει να την γράψω αναλυτικά!

Guest 018946 · 13 Αυγούστου 2011

επανερχομαι με μια πανευκολη διττετραγωνη $z^{4}+13z^{2}+6=0$

Αρχική Δημοσίευση από akis15:
παρατηρουμε οτι αν αθροισουμε τις βασεις των δυναμεων προκυπτει το μηδεν απο την euler Αν α+β+γ=0 τοτε α³+β³+γ³=3αβγ ε και μετα ολα ειναι ευκολα

δηλαδη η εξισωση εχει λυση τις χ1=2 χ2=-1 χ3=1/2 ? :hmm:

Bl4Ck_PyTh0N! · 13-08-11

Αρχική Δημοσίευση από dr.tasos:
επανερχομαι με μια πανευκολη διττετραγωνη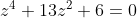 $z^{4}+13z^{2}+6=0$

Φίλε Τάσο η εξίσωση που δίνεις είναι αδύνατη στο R.Έχει 4 μιγαδικές ρίζες που είναι οι εξής : ${x}_{1}=-\frac{\sqrt{13-\sqrt{145}}i}{\sqrt{2}} , {x}_{2}=\frac{\sqrt{13-\sqrt{145}}i}{\sqrt{2}} , {x}_{3}=-\frac{\sqrt{\sqrt{145}+13}i}{\sqrt{2}}, {x}_{4}=\frac{\sqrt{\sqrt{145}+13}i}{\sqrt{2}}$

Νομίζω πως δεν ήταν άσκηση για παιδιά πρώτης Λυκείου αυτή.

(Κι εγώ βρήκα τη λύση στο Ιντερνετ διότι με παραξένεψε η φάτσα της εξίσωσης ,αφού δεν λυνόταν στο R)

Φιλικά
Γιώργος.

g1wrg0s · 13-08-11

Βασικα λεει οτι ο z ειναι μιγαδικος; Γιατι ειναι αδυνατη στο IR;

Bl4Ck_PyTh0N! · 13-08-11

Αρχική Δημοσίευση από g1wrg0s:
Βασικα λεει οτι ο z ειναι μιγαδικος; Γιατι ειναι αδυνατη στο IR;

Δε λέει ότι το Z είναι μιγαδικός.Απλά αυτή η εξίσωση είναι αδύνατη στο R.Την προσπάθησα με πολλά κόλπα και δεν έβγαινε.Με μια ματιά στο διαδίκτυο βρήκα αυτές τις 4 λύσεις της!

Guest 018946 · 13-08-11

θετω ${z}^{2}={x}$ και παιρνω ${x}^2+13{x}+6$ της οποιας οι λυσεις ειναι ${x}_{1}= \frac{-13+\sqrt[2]{145}}{12}$ και ${x}_{2}= \frac{-13-\sqrt[2]{145}}{12}$ προφανως η δευτερη και η πρωτη απορριπτεται διοτι δεν ${z}^{2}$ να ειναι αρνητικος αριθμος. Αρα θα πουμε πως απλως ειναι αδυνατη στο R .

Bl4Ck_PyTh0N! · 13 Αυγούστου 2011

Αρχική Δημοσίευση από dr.tasos:
θετω ${z}^{2}={x}$ και παιρνω ${x}^2+13{x}+6$ της οποιας οι λυσεις ειναι ${x}_{1}= \frac{-13+\sqrt[2]{145}}{12}$ και ${x}_{2}= \frac{-13-\sqrt[2]{145}}{12}$ προφανως η δευτερη απορριπτεται διοτι δεν ${z}^{2}$ να ειναι αρνητικος αριθμος.

Kάτσε ρε φίλε,τόσο απλό ήταν?Αυτά τα νούμερα εμένα με πήγαν αλλού...

Τεσπα,ανεβάζω τη λύση μου στην εξίσωση που έβαλα!

Αρχική Δημοσίευση από akis15:
παρατηρουμε οτι αν αθροισουμε τις βασεις των δυναμεων προκυπτει το μηδεν απο την euler Αν α+β+γ=0 τοτε α³+β³+γ³=3αβγ ε και μετα ολα ειναι ευκολα

Επειδή υπάρχει περίπτωση να διαβάζουν και παιδιά που δεν κατάλαβαν την εξαιρετική σου λύση σκέφτηκα να την αναρτήσω βήμα βήμα.
Έχουμε την εξίσωση ${(x-2)}^{3}+{(x+1)}^{3}+{(1-2x)}^{3}=0$ (1)

Θέτουμε : $\alpha =x-2$ , $\beta =x+1$ και $\gamma =1-2x$

Oπότε προσθέτοντας τις ποσότητες α,β,γ καταλήγουμε στο γεγονός ότι α+β+γ=0 (2).Eπίσης σύμφωνα με την (1) ισχύει ότι α³+β³+γ³=0 (3)
(2)<=> α+β=-γ <=> (α+β)³=(-γ)³ <=> α³+3α²β+3αβ²+β³=-γ³ <=> α³+β³+γ³=-3α²β-3αβ² <=> α³+β³+γ³=-3αβ(α+β) <=>(από (2) ) α³+β³+γ³=-3αβ(-γ) <=> α³+β³+γ³=3αβγ <=>(από (3)) 3αβγ=0 <=> α=0 ή β=0 ή γ=0 <=> χ-2=0 ή χ+1=0 ή 1-2χ=0 <=> χ=2 ή χ=-1 ή χ=1/2

Αυτή ήταν η λύση της εξίσωσης που είχα βάλει παραπάνω.

Guest 018946 · 13-08-11

και η πρωτη απορριπτεται

Bl4Ck_PyTh0N! · 13-08-11

Αρχική Δημοσίευση από dr.tasos:
και η πρωτη απορριπτεται

Ναι φίλε Τάσο,είναι αδύνατη στο R.Δε μπορεί να έχει μόνο μια πραγματική ρίζα και 3 μιγαδικές.Αφού πάντα οι μιγαδικές ρίζες είναι συζυγείς.Δηλαδή θα είναι τουλάχιστον 2.Στην προκειμένη περίπτωση οι μιγαδικές ρίζες είναι 4 ανά 2 συζυγείς,συνεπώς η εξίσωση είναι αδύνατη στο R.

Φιλικά
Γιώργος

Guest 018946 · 13-08-11

ναι η εξισωση ειναι οντως αδυνατη στο R .Δεν θα επρεπε να επεκταθεις σε μιγαδικους εφοσον ειναι τοπικ α λυκειου

Bl4Ck_PyTh0N! · 13-08-11

Αρχική Δημοσίευση από dr.tasos:
ναι η εξισωση ειναι οντως αδυνατη στο R .Δεν θα επρεπε να επεκταθεις σε μιγαδικους εφοσον ειναι τοπικ α λυκειου

Αν βάζεις ασκήσεις που χρειάζονται μαθηματικά α λυκείου για να λυθούν δε θα επεκτείνομαι στους μιγαδικούς!

Guest 018946 · 13-08-11

γραψε λαθος μ'αρεσει να επεκτεινεσαι περαιτερω αλλα μην θεωρεις για την λυση της ασκησης σε επιπεδο α λυκειου χρειαζονται γνωσεις γ λυκειου

Bl4Ck_PyTh0N! · 13-08-11

Αρχική Δημοσίευση από dr.tasos:
γραψε λαθος μ'αρεσει να επεκτεινεσαι περαιτερω αλλα μην θεωρεις για την λυση της ασκησης σε επιπεδο α λυκειου χρειαζονται γνωσεις γ λυκειου

Έγινε φίλε Τάσο.Αλλά χρειάζεται προσοχή πριν δώσουμε άσκηση!Εγώ που είμαι σχετικά έμπειρος το είδα.Σκέψου να τυραννιόταν ένα παιδί της Α ή της Β Λυκείου.

Guest 018946 · 13-08-11

θα ελεγε οτι ειναι αδυνατη στο R και τελος .

Συλλογή ασκήσεων στην Άλγεβρα

Δραστήριο μέλος

Guest 018946

Επισκέπτης

Δραστήριο μέλος

Δραστήριο μέλος

Διάσημο μέλος

Διάσημο μέλος

Δραστήριο μέλος

Guest 018946

Επισκέπτης

Δραστήριο μέλος

Επιφανές μέλος

Δραστήριο μέλος

Guest 018946

Επισκέπτης

Δραστήριο μέλος

Guest 018946

Επισκέπτης

Δραστήριο μέλος

Guest 018946

Επισκέπτης

Δραστήριο μέλος

Guest 018946

Επισκέπτης

Δραστήριο μέλος

Guest 018946

Επισκέπτης