

Βασικά πειράζει. Γιατί αφού μόλις τελείωσες το λύκειο, έπρεπε να αναρτηθείς αν το d είναι πραγματικός η μιγαδικός.ή
Ελπίζω πως δεν υπάρχει πρόβλημα που δεν είμαι στην α'λυκείου!
Η απάντηση στους μιγαδικούς είναι η:
Έλεγξέ το.
Ισχύει:
Αυτή είναι γελοιωδώς εύκολη ακόμη και για μαθητή Α λυκείου.οχι ρε πυθωνα κανενα προβλημα ισα ισα. ετσι σε θελω συμμετοχη στα thread της αλγεβρας α λυκειου
αυτη θα την προσπαθει κανεις γιατι αν οχι να ανεβασω την λυση . σε latex
Αυτά που έχουν κάποιο ενδιαφέρον για έναν μαθητή λυκείου είναι τα άλλα που είχες βάλει σε προηγούμενο μήνυμά σου:
ας βαλω και μια που μου φανηκε απλη : εαννα υπολογισετε το
και μια ακομα να συγκρινετε τους αριθμους :και

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


τι να σου πω τους μιγαδικους δεν τους εχω . Μονο μια γενικη ιδεα εχω τιποτα παραπανω. Οσο για τις προηγουμενες ασκησεις που εβαλα δυστυχως ποτε δεν απαντηθηκανΒασικά πειράζει. Γιατί αφού μόλις τελείωσες το λύκειο, έπρεπε να αναρτηθείς αν το d είναι πραγματικός η μιγαδικός.
Η απάντηση στους μιγαδικούς είναι η:
Έλεγξέ το.
Ισχύει:
Αυτή είναι γελοιωδώς εύκολη ακόμη και για μαθητή Α λυκείου.
Αυτά που έχουν κάποιο ενδιαφέρον για έναν μαθητή λυκείου είναι τα άλλα που είχες βάλει σε προηγούμενο μήνυμά σου:

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Polkiu
Πολύ δραστήριο μέλος


Δεν θυμάμαι να διδαχτήκαμε κάτι τέτοιο φέτος στα μαθηματικάΒασικά πειράζει. Γιατί αφού μόλις τελείωσες το λύκειο, έπρεπε να αναρτηθείς αν το d είναι πραγματικός η μιγαδικός.
Η απάντηση στους μιγαδικούς είναι η:
Έλεγξέ το.
Ισχύει: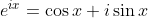

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Bl4Ck_PyTh0N!
Δραστήριο μέλος


Δεν θυμάμαι να διδαχτήκαμε κάτι τέτοιο φέτος στα μαθηματικά
όχι δεν έχουμε διδαχθεί κάτι τέτοιο.Προφανώς το παιδί exc έχει κάνει όλη την ύλη των μιγαδικών κι όχι ένα κομμάτι τους όπως εμείς.

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


καλου κακου κανε μια επαναληψη στα μαθηματικα της γ πριν πας στο λυκειοΝα ρωτησω κατι?? Αυτα ειναι σιγουρα μαθηματικα α Λυκειου? Φαινονται δυσκολα!

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Ναι το πρόσεξα ότι κανείς δεν ασχολήθηκε για αυτό τις επανέφερα.Οσο για τις προηγουμενες ασκησεις που εβαλα δυστυχως ποτε δεν απαντηθηκαν
Είναι περίπου εκτός ύλης. Δεν είπα ότι έπρεπε να το γνώριζε, είπα ότι έπρεπε να αναρωτηθεί αν το d είναι πραγματικός ή όχι πριν δώσει τη λύση, γιατί κάθε μονώνυμο βαθμού n έχει n ρίζες και βρήκε μόνο δύο για ένα 6ου βαθμού.Δεν θυμάμαι να διδαχτήκαμε κάτι τέτοιο φέτος στα μαθηματικά
Είθισται σε ένα τμήμα Φυσικής...όχι δεν έχουμε διδαχθεί κάτι τέτοιο.Προφανώς το παιδί exc έχει κάνει όλη την ύλη των μιγαδικών κι όχι ένα κομμάτι τους όπως εμείς.

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Bl4Ck_PyTh0N!
Δραστήριο μέλος


Ναι το πρόσεξα ότι κανείς δεν ασχολήθηκε για αυτό τις επανέφερα.
Είναι περίπου εκτός ύλης. Δεν είπα ότι έπρεπε να το γνώριζε, είπα ότι έπρεπε να αναρωτηθεί αν το d είναι πραγματικός ή όχι πριν δώσει τη λύση, γιατί κάθε πολυώνυμο βαθμού n έχει n ρίζες και βρήκε μόνο δύο για ένα 6ου βαθμού.
Είναι τόπικ της Α'λυκείου.Δε θέλω να πανικοβάλλω τα παιδιά με τους μιγαδικούς αριθμούς.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Δίκαιο έχεις.Είναι τόπικ της Α'λυκείου.Δε θέλω να πανικοβάλλω τα παιδιά με τους μιγαδικούς αριθμούς.
 Δεν προσπαθώ να σε μειώσω, αφού μάλιστα η λύση ήταν εκτός και από την Γ λυκείου, απλώς ήθελα να πω σε όλους ότι ένα μονώνυμο ν βαθμού έχει ν ρίζες και αυτές δεν είναι απαραίτητα πραγματικές.
Δεν προσπαθώ να σε μειώσω, αφού μάλιστα η λύση ήταν εκτός και από την Γ λυκείου, απλώς ήθελα να πω σε όλους ότι ένα μονώνυμο ν βαθμού έχει ν ρίζες και αυτές δεν είναι απαραίτητα πραγματικές.Είναι κάτι που τονίζεται κατά μία έννοια από τη β γυμνασίου όταν μαθαίνουν τον τύπο επίλυσης των δευτεροβάθμιων όταν τους λένε ότι μία εξίσωση δεν έχει ρίζες στους πραγματικούς αριθμούς ή με το ότι μία εξίσωση έχει διπλή ρίζα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


απο οτι ξερω ενα πολυωνυμο εχει το πολυ οσες πραγματικες και μιγαδικες οσες και ο βαθμος τουΔίκαιο έχεις.Δεν προσπαθώ να σε μειώσω, αφού μάλιστα η λύση ήταν εκτός και από την Γ λυκείου, απλώς ήθελα να πω σε όλους ότι ένα πολυώνυμο ν βαθμού έχει ν ρίζες και αυτές δεν είναι απαραίτητα πραγματικές.
Είναι κάτι που τονίζεται κατά μία έννοια από τη β γυμνασίου όταν μαθαίνουν τον τύπο επίλυσης των δευτεροβάθμιων όταν τους λένε ότι μία εξίσωση δεν έχει ρίζες στους πραγματικούς αριθμούς ή με το ότι μία εξίσωση έχει διπλή ρίζα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Βασικά το διόρθωσα, μιλούσα για μονώνυμα (είχα ξεχάσει την σωστή ορολογία).απο οτι ξερω ενα πολυωνυμο εχει το πολυ οσες πραγματικες και μιγαδικες οσες και ο βαθμος του
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Bl4Ck_PyTh0N!
Δραστήριο μέλος


Εdit : Έκανα λάθος στην αρίθμηση των σχέσεων.Τάσο έκανα μια προσπάθεια.Κοίταξε τη να μου πεις.Την απέδειξα με έναν τρόπο 2 βημάτων.Ακολουθεί η λύση
\leq 0 \Leftrightarrow \frac{(x+y)({x}^{2}-xy+{y}^{2})}{{x}^{2}+xy+{y}^{2}}-(x+y)\leq 0\Leftrightarrow \frac{(x+y)({x}^{2}-xy+{y}^{2})-(x+y)({x}^{2}+xy+{y}^{2})}{{x}^{2}+xy+{y}^{2}}\leq 0\Leftrightarrow \frac{(x+y)[{x}^{2}-xy+{y}^{2}-({x}^{2}+xy+{y}^{2})]}{{x}^{2}+xy+{y}^{2}}\leq 0\Leftrightarrow \frac{-2xy(x+y)}{{x}^{2}+xy+{y}^{2}}\leq 0)
Γνωρίζουμε ότι η παράσταση(1) αφού οι x και οι y είναι θετικοί πραγματικοί αριθμοί
Επίσης, αποδεικνύω ότι(2) ως εξής :
που ισχύει αφού έχουμε άθροισμα τετραγώνων
Οπότε συνδυάζοντας την (1) με τη (2) προκύπτει η ανισότητα που θέλουμε να αποδείξουμε.Α,αν την έχεις λύσει διαφορετικά,θέλω τη λύση σου. (έχω την εντύπωση ότι κάτι δεν πάει καλά στην εκφώνησή σου με την ισότητα αφού το x και το y θετικοί διάφοροι του μηδενός :O
)
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Προφανώς.αυτο που ειπα ισχυει και για μονωνυμα right?
Επίσης, ισχύει ότι κάθε πολυώνυμο μιας μεταβλητής με μιγαδικούς συντελεστές, έχει τουλάχιστον μία ρίζα στους μιγαδικούς.
Και εδώ να διευκρινίσουμε για όσους δεν το ξέρουν ότι οι πραγματικοί είναι υποσύνολο των μιγαδικών και συνεπώς όταν λέμε ότι ο a είναι μιγαδικός, δεν αποκλείουμε να είναι και ένας καθαρά πραγματικός.
---
@Bl4Ck_PyTh0N!
Βασικά γιατί δεν πολλαπλασίασες και τα δύο μέλη με τον παρανομαστή του αριστερού μέλους; Κάνε το να δεις τι βγάζεις.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Bl4Ck_PyTh0N!
Δραστήριο μέλος


Προφανώς.
Επίσης, ισχύει ότι κάθε πολυώνυμο μιας μεταβλητής με μιγαδικούς συντελεστές, έχει τουλάχιστον μία ρίζα στους μιγαδικούς.
Και εδώ να διευκρινίσουμε για όσους δεν το ξέρουν ότι οι πραγματικοί είναι υποσύνολο των μιγαδικών και συνεπώς όταν λέμε ότι ο a είναι μιγαδικός, δεν αποκλείουμε να είναι και ένας καθαρά πραγματικός.
---
@Bl4Ck_PyTh0N!
Βασικά γιατί δεν πολλαπλασίασες και τα δύο μέλη με τον παρανομαστή του αριστερού μέλους; Κάνε το να δεις τι βγάζεις.
Σχεδόν το ίδιο βγάζουμε.Απλά εγώ τα έκανα ομώνυμα πρώτα.Ουσιαστικά γι αυτό το λόγο έκανα και την δεύτερη απόδειξη.Εμένα με κολλάει η ισότητα αφού οι χ,y είναι θετικοί πραγματικοί αριθμοί διάφοροι του μηδενός.

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


η λυση μου ειναι αρκετα πιο απλη και γρηγορη απο την δικια σου κοιτα :Εdit : Έκανα λάθος στην αρίθμηση των σχέσεων.
και παιρνω
απο εδω βρισκω
και καταληγω στο
οσο για την λυση σου πως ακριβως σκοπευεις να τις συνδειασεις ? ειναι αργα δεν σκεφτομαι πολυ καλα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Bl4Ck_PyTh0N!
Δραστήριο μέλος


η λυση μου ειναι αρκετα πιο απλη και γρηγορη απο την δικια σου κοιτα :
χιαστι
και παιρνω
απο εδω βρισκω
και καταληγω στο
οσο για την λυση σου πως ακριβως σκοπευεις να τις συνδειασεις ? ειναι αργα δεν σκεφτομαι πολυ καλα.
γνωρίζοντας ότι η (1)<0 και η (2)>=0 τότε καταλήγουμε στο ότι (1)(2)=<0 άρα και ότι (1)/(2)=<0 (όπου (1) και (2) οι προηγούμενες σχέσεις που έχω στο ποστ μου).Εξαιρετική η λύση σου,κομψή!

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Ναι, η ισότητα ισχύει μόνο εφόσον ισχύει χ,y>=0.Σχεδόν το ίδιο βγάζουμε.Απλά εγώ τα έκανα ομώνυμα πρώτα.Ουσιαστικά γι αυτό το λόγο έκανα και την δεύτερη απόδειξη.Εμένα με κολλάει η ισότητα αφού οι χ,y είναι θετικοί πραγματικοί αριθμοί διάφοροι του μηδενός.
Βέβαια, αυτό που σου λέω εγώ δεν έχει καμία σχέση με αυτό που έκανες. Κοίτα:
το οποίο (τελευταίο) ισχύει για χ,y>=0.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Bl4Ck_PyTh0N!
Δραστήριο μέλος


Ναι, η ισότητα ισχύει μόνο εφόσον ισχύει χ,y>=0.
Βέβαια, αυτό που σου λέω εγώ δεν έχει καμία σχέση με αυτό που έκανες. Κοίτα:
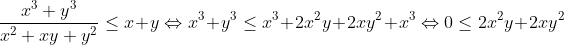
το οποίο (τελευταίο) ισχύει για χ,y>=0.
Eγώ πολλαπλασίασα με τον παρανομαστή μετά που πήγα στο α μέλος το (χ+y).Και οι δυο λύσεις είναι σωστές.

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


βλεπεις οτι αθροισμα θετικων = θετικο που ειναι
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 12 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 31 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

