tebelis13
Πολύ δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


edit: σωστός τώρα
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


Βάζω μια μικρή μην παραπονιέστεαφού την έγραψα που την έγραψα
Δίνονται οι συνεχείς συναρτήσειςμε f(x)>0, g(x)>0 για κάθε
τέτοιες ώστε να ισχύουν:
dt=\frac{1}{g(x)})
και
dt=\frac{2}{f(x)})
για κάθε
α) Να αποδείξετε ότι f(x)=2g(x) για κάθε
β) Να βρείτε τις συναρτήσεις f,g.
(Επειδή τις ασκήσεις μου τις δίνουν από φροντιστήριο και παίζει να ναι κι από κάνα βοήθημα αν σας θυμίζει τίποτα μη με πάρετε με τις ντομάτες)
λοιπόν βάζω και τη λύση να υπάρχει μιας και λύθηκε.
παραγωγίζω την (1)
τώρα τη (2)
αφού τα πρώτα είναι ίσα τότε και τα δεύτερα
για x=0 στις (1),(2) παίρνω ότι f(0)=2 και g(0)=1, άρα από την αντικατάσταση παίρνω
β) ξέρω ότι f(x)=2g(x)
από (1) παίρνω
(στο τελευταίο αντιπαραγώγησα και το c κάνει 0 )
αντίστοιχα η g(x)=f(x)/2
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
babisgr
Πολύ δραστήριο μέλος


Α) Να αποδειχθεί ότι
Β) f:R->R με
i) Η f παραγωγίσιμη στο R και να βρεθεί ο τύπος της
ii) Υπάρχει τουλάχιστον ένα
iii) Ισχύει
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dmitsos
Πολύ δραστήριο μέλος


Δίνεται συνεχής και "1-1" συνάρτηση g στοκαι μη μηδενικοί μιγαδικοί αριθμοί
για τους οποίους ισχύει:
Α) Να αποδειχθεί ότι
Β) f:R->R μενα δείξετε ότι:
i) Η f παραγωγίσιμη στο R και να βρεθεί ο τύπος της
ii) Υπάρχει τουλάχιστον ένατέτοιο, ώστε:
όπου h,p συνεχείς συναρτήσεις στο [-1,1].
iii) Ισχύειγια κάθε x στο R, να δείξετε ότι
για κάθε x στο R
Ωραία ασκησούλα!!! Πάμε!!
A)
B)
Παρατηρώ ότι το f^2(x) δε μηδενίζεται (μη μηδενικοί μιγαδικοί), άρα ούτε το f(x) και συνεπώς η f(x) διατηρεί σταθερό πρόσημο, το οποίο είναι θετικό ( μην ξεχνάμε ότι η f είναι μέτρο μιγαδικού!!). Άρα
i)
H f είναι παραγωγίσιμη ως πράξη παραγωγίσιμων.
ii) Θεωρώ τη συνάρτηση
Παρατηρώ ότι
Ακόμη f(1)=f(-1) [ Η f είναι άρτια)
Άρα από Θ.R υπάρχει k στο (-1,1) τέτοιο ώστε
iii) Βαριέμαι να γράψω λατεξ τώρα. Από την ανισότητα με Fermat παίρνουμε ότι f(0)=1. Παραγωγίζοντας την f(x) βρίσκουμε ότι για χ>0 η f είναι αύξουσα και χ<0 φθίνουσα.
Αρα χ>0 f(x)>=1
x<0 f(x) >=1.
Αυτά :p
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Άσκηση 17
Έστω
Θεωρούμε επίσης συνεχή και γνησίως αύξουσα συνάρτηση με πεδίο ορισμού και σύνολο τιμών το
α) Να δείξετε ότι
β) Η εξίσωση
γ) Να υπολογίσετε το
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Υψώνοντας τετράγωνο
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
tebelis13
Πολύ δραστήριο μέλος


Συνεχίζω την αρίθμηση από την τελευταία που ανέβασα
Άσκηση 17
Έστωμε
Θεωρούμε επίσης συνεχή και γνησίως αύξουσα συνάρτηση με πεδίο ορισμού και σύνολο τιμών το
α) Να δείξετε ότι
β) Η εξίσωσηέχει ακριβώς δύο λύσεις στο (b,c)
γ) Να υπολογίσετε το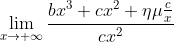
To δύσκολο ερώτημα έκανες εσύ

εφόσον
" />
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Επίσης, ξανακοίτα τις πράξεις σου στο όριο (το αποτέλεσμα είναι σωστό)
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Rempeskes
Επιφανές μέλος


γενικά το θέμα με τη μοναδικότητα είναι λίγο wtf μήπως ξέχασες να μας τη δώσεις παραγωγίσιμη την f?
γνησίως αύξουσα -> παραγωγίσιμη σε όλα τα χ, εκτός πιθανώς
επί ενος συνόλου με μηδενικό μήκος.
( lol )
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


γνησίως αύξουσα -> παραγωγίσιμη σε όλα τα χ, εκτός πιθανώς
επί ενος συνόλου με μηδενικό μήκος.
( lol )
ναι αλλά το βιβλίο δεν αναφέρει τίποτα τέτοιο πώς θα το αποδείξεις;
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Rempeskes
Επιφανές μέλος


ναι αλλά το βιβλίο δεν αναφέρει τίποτα τέτοιο πώς θα το αποδείξεις;
Eχμ...
Λέω πως θα αποδείξω
ότι το σύνολο των a οπου
lim_{a+}f - lim_{a-}f#0
μπορεί να απεικονισθεί 1-1
στο σύνολο των φυσικών.
(λολ2... προφανώς η εκφώνηση χωλαίνει)
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Και για το (γ)
γιατί το b/c είναι αρνητικό και το τελευταίο όριο δίνει μηδέν, γιατί είναι μηδενική επί φραγμένη (με απόδειξη βέβαια)
Νομίζω δεν πρέπει να ανεβάσω άλλη άσκηση, γι'αυτό θα τη δώσω να τη διαβάσετε. https://mathematica.gr/forum/viewtopic.php?f=55&t=15242
Οπότε εδώ κλείνει ο κύκλος των ασκήσεων... Έλα μη σας πιάνουν τα ζουμιά.

Ευχαριστώ όσους συμμετείχαν που βοήθησαν να μένει ενεργό το θέμα. Ελπίζω να σας άρεσαν οι ασκήσεις.
Άντε και καλή επιτυχία στις πανελλήνιες !

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Rempeskes
Επιφανές μέλος


H λύση μου για την μοναδικότητα είναι:
Εφόσον η f είναι 2ου βαθμού θα έχει το πολύ δύο λύσεις. Δείξαμε ότι η f έχει τουλάχιστον δύο λύσεις, άρα αυτές θα είναι μοναδικές
Η f είναι γνησίως αύξουσα και έχει δύο λύσεις;

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


H λύση μου για την μοναδικότητα είναι:
Εφόσον η g είναι 2ου βαθμού θα έχει το πολύ δύο λύσεις. Δείξαμε ότι η g έχει τουλάχιστον δύο λύσεις, άρα αυτές θα είναι μοναδικές
Διορθωμένο
Άσκηση 17
β) Η εξίσωσηέχει ακριβώς δύο λύσεις στο (b,c)
Επίσης στον δεύτερο όρο στον αριθμητή είναι x+f(c)
Σόρρυ ρε παίδες

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
red span
Δραστήριο μέλος


Τα μαθηματικά δεν έχουν τέλος, ούτε οι ασκήσεις
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
- Status
- Το θέμα δεν είναι ανοιχτό για νέες απαντήσεις.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 3 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

