Leo 93
Εκκολαπτόμενο μέλος


Δ) (απ΄τις αγαπημένες μου ασκήσεις)
Η συνάρτηση f είναι συνεχής στο [α,β] μεκαι
.
Να αποδείξετε ότι υπάρχει:f\left(\xi \right)=\sigma \upsilon \nu \xi )
Έστω
γιατί για x=α είναι
Άρα υπάρχει
Θεωρούμε τη συνάρτηση
Άρα (θ.Bolzano) υπάρχει
Θα δείξω ότι το c βρίσκεται στο (α,β)
f(a)>cosa, άρα c δεν είναι ίσο με το a.
(*) O παραπάνω τρόπος δεν εγγυάται ότι το c βρίσκεται στο ανοιχτό διάστημα. Μπορούμε να δουλέψουμε και ως εξής.
Ακόμη, f(a)>1>cosa.
Eφαρμόζουμε Bolzano στην
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Ας γράψω αναλυτικά τη 2η λύση σου (αν την κατάλαβα καλά)
Έστω
Έστω
Bolzano στο [α,c]
Η λύση που είχα εγώ υπόψιν
Έστω ότι
Τότε
Άρα υπάρχει ένα τουλάχιστον
Bolzano για την
Να βάλω τη λύση της Β?
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Leo 93
Εκκολαπτόμενο μέλος


Ναι, αυτό εννοούσα.Ας γράψω αναλυτικά τη 2η λύση σου (αν την κατάλαβα καλά)
Βαλ' την.Να βάλω τη λύση της Β?
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Β) Έστω συνάρτησηπαραγωγίσιμη στο [a,b] για την οποία ισχύει
Να δείξετε ότι υπάρχει=\frac{2\xi }{{b}^{2}-{a}^{2}}\int_{a}^{b}f\left(x \right)dx )
Α τρόπος
Έστω
Από το θεώρημα ενδιάμεσων τιμών για την g υπάρχει
Β τρόπος
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Αν για τους μιγαδικούς
Να δείξετε ότι

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Άσκηση 5
Αν για τους μιγαδικούςισχύουν
(1)
(2)
(3)
Να δείξετε ότι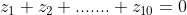
και στη 2η το ίδιο:
Αν
(4) / (5) =>

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Άσκηση 6
Έστω συνεχής συνάρτηση f:R->R για την οποία ισχύει
α) Να αποδείξετε ότι η f είναι 1-1 και να βρείτε την αντίστροφη.
β) Να αποδείξετε ότι η γραφική παράσταση της f έχει ακριβώς ένα σημείο καμπής το οποίο να βρείτε
γ) Να υπολογίσετε το
χωρίς να κάνετε αντικατάσταση (δεν με ενδιαφέρει το τελικό αποτέλεσμα, οπότε φτάστε το μέχρι ένα σημείο)
δ) Να βρείτε το πλήθος των ριζών της εξίσωσης
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


χωρίς να κάνετε αντικατάσταση
δηλαδή πώς το εννοείς, να μην αντικαταστήσουμε τίποτα μέσα στο ολοκλήρωμα με κάποια σχέση που θα έχουμε, να μην εφαρμόσουμε μέθοδο αντικατάστασης, ή απλά να μην κάνουμε τις πράξεις ( αυτό που λες στην παρένθεση) ;
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


δηλαδή πώς το εννοείς, να μην αντικαταστήσουμε τίποτα μέσα στο ολοκλήρωμα με κάποια σχέση που θα έχουμε, να μην εφαρμόσουμε μέθοδο αντικατάστασης, ή απλά να μην κάνουμε τις πράξεις ( αυτό που λες στην παρένθεση) ;
Να μην το λύσης με τη μέθοδο της αντικατάστασης.. Προσπάθησε να εκμεταλλευτείς κάποια συναρτησιακή σχέση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
tebelis13
Πολύ δραστήριο μέλος


Σωστός και γρήγορος ο Δίας !
Άσκηση 6
Έστω συνεχής συνάρτηση f:R->R για την οποία ισχύει
α) Να αποδείξετε ότι η f είναι 1-1 και να βρείτε την αντίστροφη.
β) Να αποδείξετε ότι η γραφική παράσταση της f έχει ακριβώς ένα σημείο καμπής το οποίο να βρείτε
γ) Να υπολογίσετε το
dx )
χωρίς να κάνετε αντικατάσταση (δεν με ενδιαφέρει το τελικό αποτέλεσμα, οπότε φτάστε το μέχρι ένα σημείο)
δ) Να βρείτε το πλήθος των ριζών της εξίσωσης=x )
α)
β)
γ)
δ)
που αν θεωρήσουμε συναρτηση και την μελετήσουμε θα δούμε ότι έχει μια ρίζα
p.s.:Σόρρυ παίδες δέν τα πάω πολύ καλά με το λάτεχ

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Δυσκολεύομαι να διαβάσω τη λύση σου (είναι και αργά). Θα την κοιτάξω αύριο. Πάντως ζήτησα και υπογράμμισα το ολοκλήρωμα να μη λυθεί με αντικατάσταση. Θα μου πεις ότι στις πανελλήνιες θα το λύσεις όπως θες. Απλά εδώ θέλω να δούμε μια πιο έξυπνη και ωραία λύση (που αν την σκεφτείτε εσείς ακόμα καλύτερα)
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


Άσκηση 6
Έστω συνεχής συνάρτηση f:R->R για την οποία ισχύει
γ) Να υπολογίσετε το
dx )
χωρίς να κάνετε αντικατάσταση (δεν με ενδιαφέρει το τελικό αποτέλεσμα, οπότε φτάστε το μέχρι ένα σημείο)
το f(0) κάνει 0 από την αρχική σχέση
τώρα για το f(6/5)
εδώ αν αντικαταστήσω x=6/5 και τα πάω στο πρώτο μέλος, με horner κλπ καταλήγω:
άρα f(6/5)=1 ( το άλλο δεν παίζει να χει ρίζα γιατί αφού f γν αύξουσα πρεπει να είναι μεγαλύτερο του f(0) δηλαδή θετικό)
edit: μια διόρθωση στα άκρα 6/5 αντί για 5/6
αυτό μας κάνει;
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


β)
Δείξαμε ότι f'(x)>0 άρα το πρόσημο της f'' εξαρτάται από την f.
Άρα η f έχει μοναδικό σημείο καμπής στο Α(0,f(0))
γ) Στο ολοκλήρωμα είστε σωστοί και οι δύο, χωρίς να κοίταξα πράξεις βέβαια. Βασίλη, πολύ ωραία λύση, δεν την είχα σκεφτεί.
Μπορούσες να βρεις το f(6/5) πιο εύκολα απ'την αντίστροφη. Δηλαδή: Για x=1 στον τύπο της αντίστροφης έχουμε
Η λύση που είχα εγώ στο μυαλό μου είναι:
στο οποίο έχουμε μόνο άγνωστο το ζητούμενο ολοκλήρωμα
δ)
Θέλουμε το πλήθος των ριζών της συνάρτησης
Κάνοντας πίνακα μονοτονίας έχουμε ότι η g είναι γνησίως αύξουσα στα Α1=(-οο,-1] και Α2=[1,+οο) και γνησίως φθίνουσα στο Α3=[-1,1]
Άρα η g δεν έχει ρίζα στο Α1
Άρα η g έχει μοναδική ρίζα στο Α2
Άρα η g δεν έχει ρίζα στο Α3
'Ασκηση 7
Δίνεται η f συνεχής συνάρτηση στο R, με
α) Να βρείτε το γεωμετρικό τόπο του z.
β) Να βρεθεί το όριο
γ) Αν το εμβαδόν της f με τον x'x από τη x=0 μέχρι τη x=1 είναι μικρότερο του
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
13diagoras
Δραστήριο μέλος
lowbaper92
Πολύ δραστήριο μέλος


α)
Αν |z|>1 τότε
Αν |z|<1 τότε
Άρα |z|=1
β)
κτλ
γ)
Όμως
Bolzano στο [0,1] για την h.
Άσκηση 8 (Ωραία αλλά δύσκολη άσκηση. Για να δούμε)
Έστω οι συνεχείς συναρτήσεις f,g με Df=Dg=R και ο μιγαδικός z ώστε να ισχύουν οι σχέσεις
Επίσης θεωρήστε γνωστό (πρέπει βέβαια να ξέρετε την απόδειξη) ότι
α) Να δείξετε ότι η g είναι κυρτή και να βρείτε το γεωμετρικό τόπο των εικόνων του z.
β) Να δείξετε ότι
γ) Να δείξετε ότι
δ) Να δείξετε ότι υπάρχει ένα τουλάχιστον
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Exomag
Νεοφερμένο μέλος
13diagoras
Δραστήριο μέλος



Μια διαφορετικη ,λιγο,προσεγγιση σε ορισμενα ερωτηματα:
(a)ακριβως ετσι την ελυσα.
(b)εφαρμοσα ΘΜΤ στο[0,χ].
(c)ακριβως ετσι την ελυσα,επισης.
(d)πηρα bolzano στο 0 και ενα α στο οποιο σιγουρα η διαφορα f-g ειναι αρνητικη ,αλλιως,...ατοπο. Πρακτικα η ιδια λυση.
Φιλε lowbaper92 πολυ ωραιες οι ασκησεις σου!!
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Ωραία η λύση σου ! Η άσκηση θα ήταν σίγουρα πιο δύσκολη αν δεν είχα σπάσει το τελευταίο ερώτημα σε 2 υποερωτήματα, αλλά νομίζω τότε θα ήταν λίγο τσιμπημένη.Νέο μέλος στο forum και αυτό είναι το πρώτο μου post...
Ορίστε και η λύση μου... Η άσκηση δεν ήταν τόσο δύσκολη τελικά... Εκτός βέβαια αν έχω κάνει κάποιο λάθος...
View attachment 37578
Μια παρατήρηση στη λύση σου (λεπτομέρεια βέβαια) στο (γ) ερώτημα. Το "=" στην ανισότητα ισχύει μόνο για το σημείο επαφής, άρα η συνάρτηση
Εναλλακτική λύση για το (δ)
Έστω ότι
Επειδή
Άρα θα υπάρχει
Θεωρούμε
Bolzano
Άσκηση 9
Έστω η παραγωγίσιμη συνάρτηση f:[α,β]->R με f(α)=α και f(β)=β. Αν 0<α<β να αποδείξετε ότι:
α)Υπάρχει εφαπτομένη ευθεία της γραφικής παράστασης της f, η οποία είναι παράλληλη στην ευθεία y=x.
β)Υπάρχει
γ) Υπάρχουν
δ) Αν υπάρχει η f'' και είναι συνεχής στο [α,β] και ισχύει
Και δώρο αυτή
Δίνεται συνάρτηση f παραγωγίσιμη στο R, με
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
- Status
- Το θέμα δεν είναι ανοιχτό για νέες απαντήσεις.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 3 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki





 Ορίστε και οι λύσεις μου...
Ορίστε και οι λύσεις μου...


