Βοήθεια/Απορίες στη Γεωμετρία

[Don]

παιδιά δεν καταλαβαίνς τίποτα απο την γεωμετρία....
υπάρχει κανείς που μπόρει να μοθ μά8ει τα βασικά???????

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Valandil]

Ο μόνος τρόπος για να εξοικειωθείς με την γεωμετρία είναι να λύσεις αμέτρητες ασκήσεις
Το Πάσχα πλησιάζει και έτσι θα χεις ακόμη περισσότερο χρόνο να λύσεις τόσο ασκήσεις από το βιβλίο όσο και από βοηθήματα.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Don]

ας πούμε πως τα πάω σκ*** και οτι δέν γουστάρω κα8όλου την γεωμετρία?????????
πάντωσ το πάσχα θα προσπαθήσω

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Valandil]

Αν τα πας καλά στην Άλγεβρα μικρό το κακό,αφού εκτός από την Β,δεν θα ξανακάνεις γεωμετρία στη ζωή σου :p
Αν δεν τα πας καλά κι εκεί όμως,κάτσε ψάξτο τώρα που είναι νωρίς

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Don]

άλγεβρα μια χαρα τα πάω.... σχέτικα καλα :no1:
πάντως 8α δω τι 8α κάνω.......φχάριστω μάγκα μου

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 17 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[tzoker]

Να εξετάσετε αν υπάρχει τρίγωνο με εμβαδόν ίσο με και περίμετρο ίση με .

:s

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[djimmakos]

Με δουλεύεις;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[tzoker]

Εγώ???????

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[X-FILER]

ο Μακης θα ξερει

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Boom]

Α+β+γ=12
Α=12-β-γ(1)

Α*υ=24
(12-β-γ)24/α=24
12-β-γ=α (2)



(1)=(2) αρα υπαρχει

ξερω ειναι λαθος....αλλα δν μ ερχετε κατι αλλο

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Crookshanks]

Δε γίνεται να υπάρχει τέτοιο τρίγωνο γιατί:

Εφ' όσον κάθε πλευρά του τριγώνου πρέπει να είναι μικρότερη από τις δύο άλλες, για οποιαδήποτε πλευρά χ ισχύει: χ<6

Έχουμε: Ε=β*υ/2
12=β*υ/2
24=β*υ
β=24/υ

Αλλά είπαμε πως κάθε πλευρά πρέπει να είναι μικρότερη από 6 cm, οπότε β<6 και άρα 24/υ<6. Επομένως:
24<6υ
υ<24/6
υ<4

Άρα για να ισχύει 12=β*υ/2 θα πρέπει η βάση β του τριγώνου να είναι τέτοια ώστε αν πολλαπλασιαστεί με αριθμό μικρότερο του 4 και διαιρεθεί με το 2 να μας δίνει 12. Αλλά για να ισχύει αυτό θα πρέπει β>6, πράγμα που είναι αδύνατο από την ανισοτική σχέση των πλευρών και επομένως ένα τέτοιο τρίγωνο είναι αδύνατο να υπάρξει.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[djimmakos]

Δε γίνεται να υπάρχει τέτοιο τρίγωνο γιατί:

Spoiler

Εφ' όσον κάθε πλευρά του τριγώνου πρέπει να είναι μικρότερη από τις δύο άλλες, για οποιαδήποτε πλευρά χ ισχύει: χ<6

Έχουμε: Ε=β*υ/2
12=β*υ/2
24=β*υ
β=24/υ

Αλλά είπαμε πως κάθε πλευρά πρέπει να είναι μικρότερη από 6 cm, οπότε β<6 και άρα 24/υ<6. Επομένως:
24<6υ
υ<24/6
υ<4

Άρα για να ισχύει 12=β*υ/2 θα πρέπει η βάση β του τριγώνου να είναι τέτοια ώστε αν πολλαπλασιαστεί με αριθμό μικρότερο του 4 και διαιρεθεί με το 2 να μας δίνει 12. Αλλά για να ισχύει αυτό θα πρέπει β>6, πράγμα που είναι αδύνατο από την ανισοτική σχέση των πλευρών και επομένως ένα τέτοιο τρίγωνο είναι αδύνατο να υπάρξει.

Μπορεί να είναι και ισόπλευρο το τρίγωνο

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[tzoker]

Δείτε μία κομψή λύση.

Το εμβαδόν τριγώνου δίνεται από τον τύπο όπου είναι η ημιπερίμετρος του τριγώνου και η ακτίνα του εγγεγραμμένου κύκλου στο τρίγωνο. Έτσι .

Τότε το εμβαδόν του εγγεγραμμένου στο τρίγωνο κύκλου θα είναι: .

Όμως . Δηλαδή το εμβαδόν του εγγεγραμμένου στο τρίγωνο κύκλου θα είναι μεγαλύτερο από το εμβαδόν του τριγώνου.

ΑΤΟΠΟ!!!

Άρα δεν υπάρχει τέτοιο τρίγωνο .

Σημείωση : p = π .

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Boom]

Δείτε μία κομψή λύση.

Το εμβαδόν τριγώνου δίνεται από τον τύπο όπου είναι η ημιπερίμετρος του τριγώνου και η ακτίνα του εγγεγραμένου κύκλου στο τρίγωνο. Έτσι .

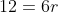
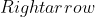
Τότε το εμβαδόν του εγγεγραμμένου στο τρίγωνο κύκλου θα είναι: .

Όμως . Δηλαδή το εμβαδόν του εγγεγραμμένου στο τρίγωνο κύκλου θα είναι μεγαλύτερο από το εμβαδόν του τριγώνου.

ΑΤΟΠΟ!!!

Άρα δεν υπάρχει τέτοιο τρίγωνο .

Σημείωση : p = π .

ναι ομως αυτον τον τυπο τν μαθαμε στ β λυκειου πως θα την λυσουν τα παιδια???χρειαζεται παραπανω γνωσεις

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[maraki]

ΠΑΡΑΚΑΛΩ??????????????????
Να ρωτήσω κτ?Αυτά τα έχουμε μάθει μέχρι τη γ γυμνασίου?????????????Γτ αν ναι ...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[tzoker]

Μα το είπα είναι κάπως πιο advanced η άσκηση. . . ο djimmakos ήθελε να υποστεί βασανισμό. . . δε φταίω εγώ!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Valandil]

Μα το είπα είναι κάπως πιο advanced η άσκηση. . . ο djimmakos ήθελε να υποστεί βασανισμό. . . δε φταίω εγώ!

Θα ήταν πολύ πιο σοφό να του έβαζες μια πιο advanced άσκηση σύμφωνα με αυτά που έχει διδαχτεί μέχρι στιγμής.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Boom]

Μα το είπα είναι κάπως πιο advanced η άσκηση. . . ο djimmakos ήθελε να υποστεί βασανισμό. . . δε φταίω εγώ!

ειπαμε να βαλεις κατι του επιπεδου τους οχι να τα πετσοκοψεις τα καημενα...ακομα δν πηγαν α' λυκειου, μν τα απογοητευεις....

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[tzoker]

Παιχνίδι κάνουμε!!!!!!!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Crookshanks]

Δε γίνεται να υπάρχει τέτοιο τρίγωνο γιατί:

Spoiler

Εφ' όσον κάθε πλευρά του τριγώνου πρέπει να είναι μικρότερη από τις δύο άλλες, για οποιαδήποτε πλευρά χ ισχύει: χ<6

Έχουμε: Ε=β*υ/2
12=β*υ/2
24=β*υ
β=24/υ

Αλλά είπαμε πως κάθε πλευρά πρέπει να είναι μικρότερη από 6 cm, οπότε β<6 και άρα 24/υ<6. Επομένως:
24<6υ
υ<24/6
υ<4

Άρα για να ισχύει 12=β*υ/2 θα πρέπει η βάση β του τριγώνου να είναι τέτοια ώστε αν πολλαπλασιαστεί με αριθμό μικρότερο του 4 και διαιρεθεί με το 2 να μας δίνει 12. Αλλά για να ισχύει αυτό θα πρέπει β>6, πράγμα που είναι αδύνατο από την ανισοτική σχέση των πλευρών και επομένως ένα τέτοιο τρίγωνο είναι αδύνατο να υπάρξει.

Βρε παιδιά, ας πει και ο τόπικ στάρτερ αν είναι η δική μου λύση σωστή...

djimmakos, ακόμα και ισόπλευρο να 'ναι το τρίγωνο ισχύουν όσα είπα.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.