Lida Ι.
Νεοφερμένο μέλος


Και εγώ κάπως έτσι το πήγα άλλα μου φαίνεται πολύ παράξενο να σου έχει συγκεκρίμενα νούμερα και να σου λέει ''αιτιολόγησε'' και να βγαίνει το αποτέλεσμα εμπειρικά μόνο!

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
natasoula...
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dark_knight
Νεοφερμένο μέλος


Μπορείς να το αιτιολογήσεις και πιο αυστηρά λύνοντας τις εξισώσεις
και βρίσκοντας τ'=2.
Όσο για την πρώτη, η μέση ταχύτητα είναι ίση με την απόσταση που διανήθηκε προς το χρόνο, δηλαδή
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Για τη δεύτερη υπάρχει μια απλή εξήγηση: Η ταχύτητα του σώματος στο διάστημαείναι μεγαλύτερη από ότι στο
. Άρα το πρώτο μισό θα το κάνει σε λιγότερο χρόνο από 6/2 και από τα πιθανά αποτελέσματα μόνο το 2 έχει αυτή την ιδιότητα.
Μπορείς να το αιτιολογήσεις και πιο αυστηρά λύνοντας τις εξισώσεις
και
και βρίσκοντας τ'=2.
Όσο για την πρώτη, η μέση ταχύτητα είναι ίση με την απόσταση που διανήθηκε προς το χρόνο, δηλαδήμε μια διαφορετική αιτιολόγηση να είναι:
.
Ετσι εξηγουνται ολα ! Μπραβο
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Lida Ι.
Νεοφερμένο μέλος


Για τη δεύτερη υπάρχει μια απλή εξήγηση: Η ταχύτητα του σώματος στο διάστημαείναι μεγαλύτερη από ότι στο
. Άρα το πρώτο μισό θα το κάνει σε λιγότερο χρόνο από 6/2 και από τα πιθανά αποτελέσματα μόνο το 2 έχει αυτή την ιδιότητα.
Μπορείς να το αιτιολογήσεις και πιο αυστηρά λύνοντας τις εξισώσεις
και
και βρίσκοντας τ'=2.
Όσο για την πρώτη, η μέση ταχύτητα είναι ίση με την απόσταση που διανήθηκε προς το χρόνο, δηλαδήμε μια διαφορετική αιτιολόγηση να είναι:
.
Ευχαριστώ πολύυυ!!!!

Πολύ ωραιες λύσεις!
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
red span
Δραστήριο μέλος


Μπορουμε να εφαρμοσουμε το Θ.Μ.Τ?(λεω εγω τωρα)Για τη δεύτερη υπάρχει μια απλή εξήγηση: Η ταχύτητα του σώματος στο διάστημαείναι μεγαλύτερη από ότι στο
. Άρα το πρώτο μισό θα το κάνει σε λιγότερο χρόνο από 6/2 και από τα πιθανά αποτελέσματα μόνο το 2 έχει αυτή την ιδιότητα.
Μπορείς να το αιτιολογήσεις και πιο αυστηρά λύνοντας τις εξισώσεις
και
και βρίσκοντας τ'=2.
Όσο για την πρώτη, η μέση ταχύτητα είναι ίση με την απόσταση που διανήθηκε προς το χρόνο, δηλαδήμε μια διαφορετική αιτιολόγηση να είναι:
.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dark_knight
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Θα προσπαθήσω να σε βοηθήσω αλλά τεχνικά μου είναι δύσκολο λόγω του μέρους που βρίσκομαι. Ετσι με λόγια έχουμε.Θα ήθελα μεγάλη βοήθεια σε δύο θεωρητικές ασκήσεις πάνω στις ταλαντώσεις.
Είναι από το βοήθημα του Άγγελου Κατσικά (Εκδόσεις Ελληνοεκδοτική)
Η πρωτη λέει:
Η μέση ταχύτητα ενός σώματος που εκτελεί αρμονική ταλάντωση κατά την απευθείας μετάβαση από τη θέση ισορροπίας στην ακραία θέση της ταλάντωσης είναι:
α) umax/2 β) umax/4 γ) umax/ρίζα 2 γ)2umax/π δ)2umax/π ε)umax/2π
Σωστή είναι το δ άλλα το θέμα είναι ότι δεν μου έρχεται καμία ιδέα για αιτιολόγηση!
Και η δεύτερη:
Αν σε χρόνο 6' ένα σώμα που εκτελεί απλή αρμονική ταλάντωση μεταβαίνει από τη θέση ισορροπίας του στην ακραία θέση, τότε σε πόσο χρόνο μεταβαίνει από τη θέση ισορροπίας του στο μισό της ακραίας θέσης;
α) 2' β)3' γ)4' δ)5'
Σωστή απάντηση είναι το α αλλά και πάλι έχω πρόβλημα με την δικαιολόγηση!
Θα παρακαλούσα αν μπορείτε να μου δώσετε τα φώτα σας!!!!
Στο πρώτο. Κρίση μου. Απαράδεκτο ως θέμα. Τώρα
Οπως ξέρεις το γινόμενο ταχύτητας - χρόνου δίνει διάστημα. Αν κάνω τη γραφική παράσταση της ταχύτητας σε άξονες υ-t (Είναι αυτό το κυπελάκι) θα υπολογίσω το εμβαδόν από 0 έως Τ/4. Πως? Μα ασφαλώς με ολοκλήρωμα 0-Τ/4 υο.συνωt.dt που βγαίνει υο.Τ/2π
και εκφράζει τη μετατόπιση. Αν το διαιρέσεις με το χρόνο που είναι ίσος με Τ/4 , έχεις τη μέση ταχύτητα=2υο/π Πως σου φάνηκε? Είναι για σας?
Το δεύτερο τώρα είναι πολύ εύκολο, αρκεί να διδάχτηκες την αρμονική κίνηση με τη βοήθεια του τριγωνομετρικού κύκλου.
Φτιάχνεις έναν τριγωνομετρικό κύκλο και σημειώνεις τη θέση του κινητού στο μέσον του άξονα των ημιτόνων. Φέρεις παράλληλο από εκεί προς τον άξονα των συνημιτόνων που τέμνει τον κύκλο δεξιά σε ένα σημείο . Ενώνεις το κέντρο με το σημείο και σχηματίζεται ορθογώνιο τρίγωνο. Βρίσκεις την μία οξεία γωνία ημφ=xo/x=1/2 ==> φ=π/6 και από τη σχέση ωt=φ βρίσκεις τον χρόνο t=2s αφού Τ/4=6s
Ελπίζω να σε βοήθησα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dark_knight
Νεοφερμένο μέλος


Φυσιολογικό και αρκετά απλό θέμα για τρίτη λυκείου. Βγαίνει και χωρίς ολοκλήρωμα.Απαράδεκτο ως θέμα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
red span
Δραστήριο μέλος


Με το Θ.Μ.Τ θα δειξουμε οτι ο μεσος ρυθμος μεταβολης ειναι ισος με τον στιγμιαιο.Αυτο που λες θα προεκυπτε με το θ.BolzanoΤο θεώρημα μέσης τιμής απλά θα μας διαβεβαιώσει ότι ηλαμβάνει κάθε τιμή του διαστήματος
, συμπεριλαμβανομένης και της
. Από αυτό πώς θα βρούμε με πόσο ισούται η
;
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mariophys
Εκκολαπτόμενο μέλος


τώρα όσο για τη δυσκολία της άσκησης, αναρωτιέμαι γιατί ένα απλό ολοκήρωμα έχει καταντήσει να θεωρείται εξεζητημένο θέμα; Δηλαδή τι, πρέπει να μείνουμε στους τύπους της ομαλής κίνησης; Αυτό δεν εαποτελεί εξάσκηση του μαθητή, είναι για να δουλεύουν οι φροντηστηριάδες και να σας παπαγαλίζουν ασκήσεις. Προσωπική άποψη, εξαιρετικό θέμα μέτριας δυσκολίας.
Με το Θ.Μ.Τ θα δειξουμε οτι ο μεσος ρυθμος μεταβολης ειναι ισος με τον στιγμιαιο.Αυτο που λες θα προεκυπτε με το θ.Bolzano
Σε καμία περίπτωση, η ταχύτητα μεταβάλλεται σε κάθε χρονική στιγμή, η δε μέση τιμή της είναι άλλο θέμα. Ξαναδιάβασε τη θεωρία της απλής αρμονικής ταλάντωσης.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
red span
Δραστήριο μέλος


Εγω μια χαρα την ξερω την θεωρια της απλης αρμονικης ταλαντωσης.Το Θ.Βολζανο δινει σημαντικες πληροφοριες στην α.α.τ,(στο οτι η κινητικη γινεται ιση με την κινητικη 4 φορες σε μια περιοδο).Τα παιδια που τωρα αρχιζουν την Γ λυκειου που στο διαολο να ξερουν τα ολοκληρωματα ρε μαγκα.Η απλή και πολύ εύληπτυ λύση είναι σαφώς ο ευθύς προσδιορισμός το χρονικού διαστήματος μέσω της ολοκλήρωσης. Όλες οι άλλες μέθοδοι δεν αποτελούν παρά προσεγγιστικές λύσεις ή εν πάσει περιπτώσει ξεφεύγουν απο τη φυσική σκέψη. Όταν κάνετε φυσική ξεχάστε τα θεωρήματα Bolzano μέσης τιμής και τις λοιπές βλακείες, σας είναι παντελώς άχρηστα.
τώρα όσο για τη δυσκολία της άσκησης, αναρωτιέμαι γιατί ένα απλό ολοκήρωμα έχει καταντήσει να θεωρείται εξεζητημένο θέμα; Δηλαδή τι, πρέπει να μείνουμε στους τύπους της ομαλής κίνησης; Αυτό δεν εαποτελεί εξάσκηση του μαθητή, είναι για να δουλεύουν οι φροντηστηριάδες και να σας παπαγαλίζουν ασκήσεις. Προσωπική άποψη, εξαιρετικό θέμα μέτριας δυσκολίας.
Σε καμία περίπτωση, η ταχύτητα μεταβάλλεται σε κάθε χρονική στιγμή, η δε μέση τιμή της είναι άλλο θέμα. Ξαναδιάβασε τη θεωρία της απλής αρμονικής ταλάντωσης.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dark_knight
Νεοφερμένο μέλος


Το οποίο θα σου δώσειΜε το Θ.Μ.Τ θα δειξουμε οτι ο μεσος ρυθμος μεταβολης ειναι ισος με τον στιγμιαιο
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Lida Ι.
Νεοφερμένο μέλος


Ευχαριστώ πολύ για τις λύσεις σου!!!Το δεύτερο τώρα είναι πολύ εύκολο, αρκεί να διδάχτηκες την αρμονική κίνηση με τη βοήθεια του τριγωνομετρικού κύκλου.
Φτιάχνεις έναν τριγωνομετρικό κύκλο και σημειώνεις τη θέση του κινητού στο μέσον του άξονα των ημιτόνων. Φέρεις παράλληλο από εκεί προς τον άξονα των συνημιτόνων που τέμνει τον κύκλο δεξιά σε ένα σημείο . Ενώνεις το κέντρο με το σημείο και σχηματίζεται ορθογώνιο τρίγωνο. Βρίσκεις την μία οξεία γωνία ημφ=xo/x=1/2 ==> φ=π/6 και από τη σχέση ωt=φ βρίσκεις τον χρόνο t=2s αφού Τ/4=6s
Ελπίζω να σε βοήθησα.
Mε βοήθησες πολύ με τη δέυτερη! Δεν το σκέφτηκα καν το περιστρεφόμενο διάνυσμα!
Δυστυχώς παιδία ακόμα ολοκληρώματα και θεωρήματα Βolzano δεν έχουμε κάνει!!
Δεν μπορώ να τα χρησιμοποιήσω λοιπόν!
H λύση του dark night με την απόσταση που διανύθηκε προς το χρόνο που φαίνεται η πιο προσιτη για το επίπεδο των μαθηματικών μέχρι τώρα!
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mariophys
Εκκολαπτόμενο μέλος


Με το Θ.Μ.Τ θα δειξουμε οτι ο μεσος ρυθμος μεταβολης ειναι ισος με τον στιγμιαιο.Αυτο που λες θα προεκυπτε με το θ.Bolzano
Εγω μια χαρα την ξερω την θεωρια της απλης αρμονικης ταλαντωσης.Το Θ.Βολζανο δινει σημαντικες πληροφοριες στην α.α.τ,(στο οτι η κινητικη γινεται ιση με την κινητικη 4 φορες σε μια περιοδο).Τα παιδια που τωρα αρχιζουν την Γ λυκειου που στο διαολο να ξερουν τα ολοκληρωματα ρε μαγκα.
Μα προφανως η άσκηση δεν απευθύνεται σε κάποιον που ξεκινά τώρα αλλά για κάποιον που πάει για εξετάσεις. Μιλάμε για θέμα μέτριας δυσκολίας. Εαν όπως λες γνώριζες α.α.τ δεν θα έλεγες οτι ο μέσος ρυθμος μεταβολής ισούται με το στιγμιαίο. Πρώτα πρώτα ποιος ρυθμός μεταβολής. Της θέσης; της ταχύτητας; Εν πάσει περιπτώσει για να μη λέμε λάθος πράγματα. Η στιγμιαίτα ταχύτητα είναι κάθε στιγμή διαφορετική, και αυτό γιατί κάθε στιγμή ασκείται δύναμη επαναφοράς στην ταλάντωση, εκτός απο τις θέσεις ισορροπίας. Η επιτάχυνση είναι επίσης μεταβλητή καθώς στις περιπτώσεις α.α.τ η δύναμη πάντα παρουσιάζει εξάρτηση απο τη μετατόπιση, και αυτό αποτελεί γενικό νόμο όχι μόνο για την περιπτωση ταλάντωσης με ελατήρια αλλά για κάθε φαινόμενο αμείωτης ταλάντωσης. "Ρε μάγκα"
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Αναθεωρώ τις πρώτες κρίσεις μου.
Στο πρώτο θέμα: Από τον ορισμό της μέσης ταχύτητας υ=x/(T/4)=xo.4/(2π/ω)=2ω.xo/π=2υο/π
Το δεύτερο τώρα είναι πολύ εύκολο, αρκεί να διδάχτηκες την αρμονική κίνηση με τη βοήθεια του τριγωνομετρικού κύκλου.
Φτιάχνεις έναν τριγωνομετρικό κύκλο και σημειώνεις τη θέση του κινητού στο μέσον του άξονα των ημιτόνων. Φέρεις παράλληλο από εκεί προς τον άξονα των συνημιτόνων που τέμνει τον κύκλο δεξιά σε ένα σημείο . Ενώνεις το κέντρο με το σημείο και σχηματίζεται ορθογώνιο τρίγωνο. Βρίσκεις την μία οξεία γωνία ημφ=xo/x=1/2 ==> φ=π/6 και από τη σχέση ωt=φ βρίσκεις τον χρόνο t=2s αφού Τ/4=6s
Αν πάλι θέλεις να το λύσεις με τριγωνομετρικές εξισώσεις καμία αντίρρηση. Μία φορά με x=xo στην x=xoημωt για t=6s και βρίσκεις την περίοδο ότι Τ=24s και για x=xo/2 στην ίδια και βρίσκεις το ζητούμενο. Εδώ θα βρεις δύο τιμές χρόνου που αντιστοιχούν στη θέση αυτή , όταν απομακρύνεται από τη ΘΙ και όταν πλησιάζει. Στην πρώτη αντιστοιχεί ο μικρότερος χρόνος και στη δεύτερη ο μεγαλύτερος.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


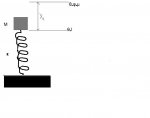
Στο ελεύθερο άκρο κατακόρυφου ελατηρίου σταθεράς k είναι δεμένο ένα σώμα μάζας m, το οποίο ισορροπεί ακίνητο και το ελατήριο έχει συσπειρωθεί κατά χ1 , όπως φαίνεται στο σχήμα. Με τη βοήθεια κατακόρυφης μεταβλητής δύναμης F μετακινούμε το σώμα προς τα κάτω, ώστε το ελατήριο να συσπειρωθεί επιπλέον κατά χ2 , και τη στιγμή εκείνη καταργούμε τη δύναμη F, οπότε το σώμα αρχίζει να εκτελεί απλή αρμονική ταλάντωση ενέργειας ΕΤ. Το έργο της μεταβλητής δύναμης υπολογίζεται από τη σχέση:
α) WF= ET-mgx1
β)WF= ET+mgx2
γ) WF= ET
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
qwerty111
Πολύ δραστήριο μέλος


Χρησιμοποίησε και τη σχέση mg=kx1
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


Ευχαριστώ πολύ!Εφάρμοσε ΘΕΕ: Κμετά - Κπριν=Ww+WFel+WF ή 0-0=...
Χρησιμοποίησε και τη σχέση mg=kx1
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 5 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 313 μέλη διάβασαν αυτό το θέμα:
- ck_chrysiis
- trifasikodiavasma
- lyfestyle.123
- GV221
- myrtle09
- Reader
- Unboxholics
- BillyTheKid
- Μήτσος10
- jellojina
- Hased Babis
- Joji
- Corfu kitty
- Maynard
- BatGuin
- KonstantinosP
- jYanniss
- exotic xo
- Qwerty 0
- userguest
- ioanna2007
- suaimhneas
- Debugging_Demon
- panosT436
- bibliofagos
- Scandal
- bboys
- georgetherrr
- Ness
- sophiaa
- mir
- Than003
- Vasilis125
- pnf292
- synthnightingale
- sakplat
- iiTzArismaltor_
- Chrisphys
- thepigod762
- Nala
- Γατέχων
- vasilis2000
- peter347
- Sofos Gerontas
- chester20080
- Greg25
- woasibe
- Magigi
- angela_k
- BiteTheDust
- Startx0
- MR WHITE
- Panatha mono
- bill09876
- Wonderkid
- Marel
- Chris180
- Claire05
- TheNorth
- estrela
- Marianna.diamanti
- love_to_learn
- carnage
- sotirislk
- ένας τυχαίος
- Lifelong Learner
- Jimpower
- Kate1914
- phleidhs
- Chemwizard
- Mara2004
- GeorgeKarag
- phoni
- Mary06
- Lia 2006
- Νομάρχης
- Γιώτα Γιαννακού
- PanosApo
- Ilovemycats27
- Jesse_
- Leo komm
- Anonymous1
- giannis256
- spring day
- Mewmaw
- Mariamar
- Pharmacist01
- Kitana
- Vicky13
- mitskification
- ΜΑΡΙΠΟΖΑ
- denjerwtithelwhelp
- Abiogenesis
- arko
- arapakos
- Marcos.Kis
- Nick_nt
- Alexecon1991
- Physicsstudent
- anna05
- katia.m
- Deneimaikala
- shezza94
- Fanimaid123
- το κοριτσι του μαη
- user-2
- tsiobieman
- Alex53
- Helen06
- T C
- eukleidhs1821
- VFD59
- xrisamikol
- lepipini
- ioanna06
- PanosBat
- rempelos42
- koukdespoina2004
- Antzie
- george777
- User2350
- qwertyuiop
- marioushi
- Nic Papalitsas
- menual
- oups
- Applepie
- eirinipap
- Jojo K
- ggl
- margik
- desp1naa
- walterrwhite
- JoannaVas
- ismember
- P.Dam.
- Χάρις
- penelopenick
- rosemary
- Steliosgkougkou
- the purge
- AnnaRd
- Signor Positivo
- onion
- cinnamongirl
- mister
- thenutritionist
- angies
- sophia<3
- Peter Pan13
- angeloskar
- Georgek7
- tapeinoxamomilaki
- Ιωάννης1234
- Praxis
- Mariahj
- Τρελας123
- Sherlockina
- Παναρας
- DimitrisGk
- Ελεν
- giannhs2001
- Idontknoww
- anakiriak@yahoo
- mpapa
- BlackBetty97
- ager
- kost28
- Eirinakiii8
- Cat lady
- Marple
- χημεια4λαιφ
- Apocalypse
- Valeris
- Vask
- Ioanna98
- ougka pougka
- GeorgePap2003
- Johanna Mark
- bruh_234
- augustine
- alpha.kappa
- Hermione granger
- constansn
- emilyfan85
- 2005
- George.S
- Dion G.
- SlimShady
- Corn90
- Meow
- Phys39
- Nick0007
- Nikoletaant
- Ameliak
- beckyy
- Rina
- Athens2002
- Eleni:
- Specon
- elenaaa
- Αντικειμενικός
- Mariaathens
- panosveki
- Superhuman
- GStef
- Gewrgia!
- papa2g
- Σωτηρία
- antonis97
- Georgekk
- Theodora03
- vetas
- _Aggelos123
- Κώστας 7708
- Alexandros973
- Cortes
- Katerinaki13
- Jimmy20
- igeorgeoikonomo
- KaterinaL
- thecrazycretan
- alexandra_
- StavMed
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki