

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Manthak47
Νεοφερμένο μέλος


Πηρα εκεινη τη σχεση επειδη απτο α ερωτημα απεδειξα οτι κανει αατ! Προσεχε στο σχημα το ΦΜ δεν θα ειναι στην ιδια θεση με την ΘΙ λογω της δυναμης που ασκειται στο σωμα,οποτε πρπ να σχεδιασεις το σωμα 3 φορες στο ΦΜ στη ΘΙ που απεχει χ1 απτο ΦΜ και σε μια τυχαι που απεχει χ,μετα πηρα για την ΘΙ ΣF=Ο,F-Fελ=ο ή F=Fel=K.x1
στην ΤΘ F-Fελ'=F-K.(x1+x) ή ΣF=F -kx1-kx αλλα η F=k.x1 οποτε K.x1-kx1-kx αρα ΣF=-kx
Noμιζω ετσι πρπ να ειναι
Ευχαριστώ πολύ
 Τη θέση ισορροπίας την είχα βάλει σε άλλη θέση από τη ΘΦΜ, αλλά δεν πήρα ΣF για ΘΙ!
Τη θέση ισορροπίας την είχα βάλει σε άλλη θέση από τη ΘΦΜ, αλλά δεν πήρα ΣF για ΘΙ!Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Μπορείς (και όλοι μπορείτε δηλαδή) να παρακολουθήσεις τη συζήτηση που είχαμε στο forum του Φυσικού ΕΚΠΑ σχετικά με την άσκηση με τη μετάβαση από το οριζόντιο στο κεκλιμένο επίπεδο (τα νεότερα μηνύματα εμφανίζονται πρώτα): https://web.cc.uoa.gr/~ctrikali/discus/messages/5065/12569.html?1270500569
Σημ.: Ο Χ. Τρικαλινός είναι πρώην αναπληρωτής καθηγητής του Φυσικού ΕΚΠΑ και νυν αναπληρωτής καθηγητής στο ΜΙΘΕ ΕΚΠΑ.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Σ΄ευχαριστώ πολύ για το ενδιαφέρον σου....συζήτηση που είχαμε στο forum του Φυσικού ΕΚΠΑ σχετικά με την άσκηση με τη μετάβαση από το οριζόντιο στο κεκλιμένο επίπεδο.......
 .
.Διάβασα με προσοχή όλη τη συζήτηση. (Ενδιαφέρον και το φόρουμ σας αλλά πολύ λίγα μπορώ να καταλάβω από όλα τα θέματα
 ). Πολύ ενδιαφέρουσα είναι η σελίδα αυτού του Κασέτα. Έχει πολύ πράμα για διάβασμα (την έβαλα στα αγαπημένα μου). Φεύγω όμως από το θέμα.
). Πολύ ενδιαφέρουσα είναι η σελίδα αυτού του Κασέτα. Έχει πολύ πράμα για διάβασμα (την έβαλα στα αγαπημένα μου). Φεύγω όμως από το θέμα.Τελικά σίγουρα από τον Κασέτα την είχε πάρει την άσκηση ο φυσικός του φίλου μου (ίδια ακριβώς εμφάνιση). Αλλά και η λύση που τους έδωσε ήταν ίδια με του Κασέτα. Για τη λύση του Κασέτα: αυτός κάνει το πρώτο λάθος που βρήκες εσύ δλδ παίρνει λέει διατήρηση στροφορμής ως πρός το σημείο σύγκρουσης αλλά τη στροφορμή λόγω περιστροφής ως προς το κέντρο. Λέει βέβαια με πιο μικρά ότι η στροφορμή είναι ίδια ως προς κάθε σημείο αλλά δεν το δικαιολογεί. (Αν θυμάσαι βέβαια εγώ στη δική μου διορθωμένη λύση έβγαλα ότι η στροφορμή είναι η ίδια και ως προς τα 2 σημεία αλλά αυτό βγαίνει μόνο αν είναι στεφάνι και όχι κάτι άλλο). Τελικά το βασικό πρόβλημα είναι η ροπή του βάρους. (Τη δική μου σκέψη, δλδ ότι το στεφάνι ακουμπά και στα 2 σημαία δεν την είπε κανένας, άρα βλακεία θα είναι
 ). Ο καθηγητής σου λέει ότι η λύση στέκει μόνον αν το βάρος θεωρηθεί αμελητέο σε σχέση με τη δύναμη της σύγκρουσης (κάπου αυτό αν δεις το έγραψα λίγο αλλά όχι σοβαρά
). Ο καθηγητής σου λέει ότι η λύση στέκει μόνον αν το βάρος θεωρηθεί αμελητέο σε σχέση με τη δύναμη της σύγκρουσης (κάπου αυτό αν δεις το έγραψα λίγο αλλά όχι σοβαρά  ). Λογικό μου ακούγεται (αυτό δεν κάνουμε και στις κανονικές κρούσεις?). Πάντως όλοι οι δικοί σου συμφώνησαν ότι η ταχύτητα δεν μπορεί να μένει ίδια (άρα οι ασκήσεις που τη θεωρούν ίδια τι λένε?
). Λογικό μου ακούγεται (αυτό δεν κάνουμε και στις κανονικές κρούσεις?). Πάντως όλοι οι δικοί σου συμφώνησαν ότι η ταχύτητα δεν μπορεί να μένει ίδια (άρα οι ασκήσεις που τη θεωρούν ίδια τι λένε? ).
).Ο φίλος μου έδωσε στον φυσικό του τη δική μου τελευταία λύση και αυτός την πήρε να την μελετήσει λέει. (Εγώ θα δώσω από Δευτέρα την άσκηση στους δικούς μου σχολείο και ιδιαίτερο). Πάντως τέτοια άσκηση που μπερδέυει και φυσικούς και προβληματίζει και καθηγητές πανεπιστημίων δεν νομίζω να είναι για πανελλήνιες. Τελικά νομίζω ήταν ωραίο που ασχοληθήκαμε και νομίζω ότι κάτι ωφελήθηκα
 .
.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
xara ths zwhsss
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Alloc
Νεοφερμένο μέλος


K=U ισχύει όταν χ= + Α/(2^1/2) ή χ=- Α/(2^(1/2)) οπου 2^(1/2) σημαινει απλά "ριζα του 2"
η αποδειξη βγαινει αν πεις οτι Ε=Κ+U αρα Κ=Ε-U
αρα πας στο Κ=U και βαζεις όπου Κ το Ε-U kai βγαίνει Ε-U=U --> E=2U---> (K*A^2)/2= K*x^2 και λύνεις ως προς χ
[FONT="]
[/FONT]
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
soares
Νεοφερμένο μέλος


α)ενας ταλαντωτης εκτελει γραμμικη αρμονικη ταλαντωση με ολικη ενεργεια 4j.Τη χρονικη στιγμη t=0 η κινητικη ενεργεια ειναι 3 j και εχει αρνητικο ρυθμο μεταβολης.Ποια η αρχικη φαση?
β)Κατακορυφο ελατηριο εχει το ενα ακρο στερεωμενο στο δαπεδο και ειναι συσπειρωμενο κατα 0,1m οταν πανω σε αυτο τοποθετηθει σωμα μαζας m και το συστημα ισοροπει.Αν g=10 m/s^2 ποση η περιοδος ταλαντωσης οταν το συστημα διαγειρεται σε ταλαντωση?
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


(Τώρα άρχισα ταλαντώσεις και δεν ξέρω ακόμα ενέργεια ταλάντωσης. Γιαυτό θα απαντήσω μόνο στο β)β)Κατακορυφο ελατηριο εχει το ενα ακρο στερεωμενο στο δαπεδο και ειναι συσπειρωμενο κατα d = 0,1m οταν πανω σε αυτο τοποθετηθει σωμα μαζας m και το συστημα ισοροπει.Αν g=10 m/s² ποση η περιοδος ταλαντωσης οταν το συστημα διαγειρεται σε ταλαντωση?
Από ισορροπία: ΣF = 0 ==> Fελ = Β ==> k·d = m·g ==> m/k = d/g ①
Περίοδος ταλάντωσης: Τ = 2π√m̅∕̅k̅ και από ① έχω Τ = 2π√d̅/̅g̅ = 2·3,14·0,1 = 0,628s

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
μακροΠΟΥΛΟΣ
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Pandemonium
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
svourikos
Νεοφερμένο μέλος




Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Παιδια οποιος μπορει ας λυσει αυτην την ασκηση .. την χρειαζομαι επιγοντως. Ευχαριστω προκαταβολικα

①+② ==> F = 3/2 m.αcm = 30N
β) Ν = Β = mg = 10Ν , ② => Τ = 10Ν
κύλιση χωρίς ολίσθηση => Τ = στατική => Τ ≤ μ.Ν => μ ≥ Τ/Ν => μ ≥ 1
γ) l = ½ αcm.t² ==> t = 2s , υcm = αcm.t = 4m/s , ω = υcm/R = 20r/s , Ι = ½ mR² = 0,2kg.m²
K = Kμετ + Κπερ = ½ m υcm² + ½ Ιω² = 120J
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Θέλω να αποδείξω ότι το σώμα θα κάνει ΑΑΤ. Όμως δεν θέλω να το κάνω με το ισοδύναμο k (αυτό ξέρω να το κάνω). Θέλω να το αποδείξω με δυνάμεις στο σώμα και τελικά να βγεί το ΣF = -D.χ και από εδώ να βρω το D = k1k2/(k1+k2). Μπερδεύομαι με τις δυνάμεις και τις επιμηκύνσεις. Μπορεί κάποιος να με βοηθήσει?
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Αν απομακρύνουμε από τη θέση ισορροπίας το σώμα και το κρατάμε σταθερό σε εκείνη τη θέση, ασκούμε πάνω του μία δύναμη F. Εμείς θέλουμε να βρούμε πόση είναι η νέα σταθερά του ελατηρίου που πρέπει να βάλουμε για να αντικαταστήσουμε τα δύο ελατήρια από ένα σταθεράς k. Άρα η δύναμη F ισούται με kx, όπου x η απομάκρυνση από τη θέση ισορροπίας / φυσικού μήκους.
Θέλω να αποδείξω ότι το σώμα θα κάνει ΑΑΤ. Όμως δεν θέλω να το κάνω με το ισοδύναμο k (αυτό ξέρω να το κάνω). Θέλω να το αποδείξω με δυνάμεις στο σώμα και τελικά να βγεί το ΣF = -D.χ και από εδώ να βρω το D = k1k2/(k1+k2). Μπερδεύομαι με τις δυνάμεις και τις επιμηκύνσεις. Μπορεί κάποιος να με βοηθήσει?
Δεδομένου ότι τα δύο ελατήρια από τη στιγμή που απλώς θα συντηρούμε την απομάκρυνση ασκώντας δύναμη F, ούτε επιμηκύνονται/μικραίνουν ούτε κινούνται στο χώρο (και υποθέτωντας ότι έχουν αμελητέα μάζα) προφανώς οι δυνάμεις στα άκρα των ελατηρίων θα είναι όλες ίσες μεταξύ τους.
Αν ονομάσουμε χ1 την επιμήκυνση του k1 και χ2 του k2, έχουμε:
k1x1=k2x2
και αν έχουμε: x1=ax2 τότε: k1a=k2
F=1/2(F1+F2)=>
2k(x1+x2)=k1x1+k2x2=>
2kax2+2kx2=k1ax2+k2x2=>
k=k2/(a+1)=>
k=k1k2/(k1+k2), αφού a=k2/k1.
Εννοείται ότι επειδή τα ανύσματα χ και F είναι αντίρροπα, έχουμε: F=-kx.
ΥΓ: Πώς εννοείς ότι ξέρεις να βρεις το ισοδύναμο k χωρίς την εξίσωση δυνάμεων κλπ;
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Αν απομακρύνουμε από τη θέση ισορροπίας το σώμα και το κρατάμε σταθερό σε εκείνη τη θέση, ασκούμε πάνω του μία δύναμη F. Εμείς θέλουμε να βρούμε πόση είναι η νέα σταθερά του ελατηρίου που πρέπει να βάλουμε για να αντικαταστήσουμε τα δύο ελατήρια από ένα σταθεράς k. ..................... ΥΓ: Πώς εννοείς ότι ξέρεις να βρεις το ισοδύναμο k χωρίς την εξίσωση δυνάμεων κλπ;
 Σε ευχαριστώ αλλά δεν ήθελα τέτοια λύση. Τέτοια περίπου έκανα κι εγώ:
Σε ευχαριστώ αλλά δεν ήθελα τέτοια λύση. Τέτοια περίπου έκανα κι εγώ:Σε ισορροπία: χ = χ1 + χ2 = F/k1 + F/k2 = F.(1/k1 + 1/k2) = F.(k1+k2)/(k1.k2) ==>
F = [(k1.k2)/(k1+k2)].x , άρα kολ = (k1.k2)/(k1+k2) κλπ.
 Αυτό εννοώ ότι ξέρω να τι κάνω. Θέλω όμως να λύσω την άσκηση ταλαντωτικά: δλδ όχι αντικαταστώντας τα ελατήρια από ένα με kολ όπως κάναμε και οι δύο. Αλλά θέλω για την τυχαία θέση χ κατά τη διάρκεια της ταλάντωσης (και όχι σε ισορροπία) να αποδείξω ότι F = -D.x από όπου να βγει ότι το D = (k1.k2)/(k1+k2). Ελπίζω να έγινα κατανοητός. Ζητάω (πάλι) πολλά?
Αυτό εννοώ ότι ξέρω να τι κάνω. Θέλω όμως να λύσω την άσκηση ταλαντωτικά: δλδ όχι αντικαταστώντας τα ελατήρια από ένα με kολ όπως κάναμε και οι δύο. Αλλά θέλω για την τυχαία θέση χ κατά τη διάρκεια της ταλάντωσης (και όχι σε ισορροπία) να αποδείξω ότι F = -D.x από όπου να βγει ότι το D = (k1.k2)/(k1+k2). Ελπίζω να έγινα κατανοητός. Ζητάω (πάλι) πολλά? 

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Τεχνικά λοιπόν, μπορείς να έχεις ισορροπία όπου θέλεις και να καταλήγεις για κάθε σημείο τη σχέση που σου είπα.
Το να καταλήξεις στην τελική σχέση F=-kx όπου k=... είναι μία απόλυτα -όπως θες να την ονομάζεις- "ταλαντωτική" λύση.
Έχεις μία σχέση που επιδέχεται ως φυσική λύση της μόνο την ταλάντωση:
ΥΓ: Τι ορίζεις εσύ ως "ταλαντωτική λύση";
---
Καθόλου κατανοητός!Αρχική Δημοσίευση από Dias:Ελπίζω να έγινα κατανοητός.

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Τι ορίζεις εσύ ως "ταλαντωτική λύση"; Καθόλου κατανοητός!
*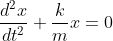
 Νομίζω βρήκα η λύση που ήθελα. Θέλω τη γνώμη και τη δική σου και όποιου άλλου θέλει.
Νομίζω βρήκα η λύση που ήθελα. Θέλω τη γνώμη και τη δική σου και όποιου άλλου θέλει.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
soares
Νεοφερμένο μέλος


Σε μια φθινουσα ηλεκτρικη ταλαντωση τη χρονικη στιγμη t=0 το πλατος ειναι Ao .Aν το πλατος μεταβαλλεται εκθετικα με το χρονο (Α=Αοe^lt) και σε χρονο τ το πλατος της ταλαντωςης γινεται Ao/2 ,ποιο ειναι το πλατος της ταλαντωσης τη χρονικη στιγμη t=4τ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Rania.
Πολύ δραστήριο μέλος


εχω μια απορια ελπιζω να βοηθησετε....
Σε μια φθινουσα ηλεκτρικη ταλαντωση τη χρονικη στιγμη t=0 το πλατος ειναι Ao .Aν το πλατος μεταβαλλεται εκθετικα με το χρονο (Α=Αοe^lt) και σε χρονο τ το πλατος της ταλαντωςης γινεται Ao/2 ,ποιο ειναι το πλατος της ταλαντωσης τη χρονικη στιγμη t=4τ?
Βαζεις οπου t το τ και οπου A το Αο\2 οποτε βρισκεις το τ, ξαναπαιρνεις τη σχεση και βαζεις οπου t το 4τ (θα γινει και απλοποιηση με τα Λ αν αυτο σε αγχωνει
 ), αρα βρισκεις το A.
), αρα βρισκεις το A.Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Alloc
Νεοφερμένο μέλος


A=Ao*e^(-Λt)
t=Τ, A= Ao/2: Ao/2=Ao*e^(-ΛΤ), e^(-ΛΤ)= 1/2 , lne^(-ΛΤ)= ln1-ln2, -ΛΤ= -ln2, T= ln2/Λ
t=4T : Α=Αο*e^(-4Λ*ln2/Λ)= Αο*e^(-4ln2)= Ao/e^(4ln2).
Εάν είναι λάθος, διορθώστε με.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 12 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 313 μέλη διάβασαν αυτό το θέμα:
- ck_chrysiis
- trifasikodiavasma
- lyfestyle.123
- GV221
- myrtle09
- Reader
- Unboxholics
- BillyTheKid
- Μήτσος10
- jellojina
- Hased Babis
- Joji
- Corfu kitty
- Maynard
- BatGuin
- KonstantinosP
- jYanniss
- exotic xo
- Qwerty 0
- userguest
- ioanna2007
- suaimhneas
- Debugging_Demon
- panosT436
- bibliofagos
- Scandal
- bboys
- georgetherrr
- Ness
- sophiaa
- mir
- Than003
- Vasilis125
- pnf292
- synthnightingale
- sakplat
- iiTzArismaltor_
- Chrisphys
- thepigod762
- Nala
- Γατέχων
- vasilis2000
- peter347
- Sofos Gerontas
- chester20080
- Greg25
- woasibe
- Magigi
- angela_k
- BiteTheDust
- Startx0
- MR WHITE
- Panatha mono
- bill09876
- Wonderkid
- Marel
- Chris180
- Claire05
- TheNorth
- estrela
- Marianna.diamanti
- love_to_learn
- carnage
- sotirislk
- ένας τυχαίος
- Lifelong Learner
- Jimpower
- Kate1914
- phleidhs
- Chemwizard
- Mara2004
- GeorgeKarag
- phoni
- Mary06
- Lia 2006
- Νομάρχης
- Γιώτα Γιαννακού
- PanosApo
- Ilovemycats27
- Jesse_
- Leo komm
- Anonymous1
- giannis256
- spring day
- Mewmaw
- Mariamar
- Pharmacist01
- Kitana
- Vicky13
- mitskification
- ΜΑΡΙΠΟΖΑ
- denjerwtithelwhelp
- Abiogenesis
- arko
- arapakos
- Marcos.Kis
- Nick_nt
- Alexecon1991
- Physicsstudent
- anna05
- katia.m
- Deneimaikala
- shezza94
- Fanimaid123
- το κοριτσι του μαη
- user-2
- tsiobieman
- Alex53
- Helen06
- T C
- eukleidhs1821
- VFD59
- xrisamikol
- lepipini
- ioanna06
- PanosBat
- rempelos42
- koukdespoina2004
- Antzie
- george777
- User2350
- qwertyuiop
- marioushi
- Nic Papalitsas
- menual
- oups
- Applepie
- eirinipap
- Jojo K
- ggl
- margik
- desp1naa
- walterrwhite
- JoannaVas
- ismember
- P.Dam.
- Χάρις
- penelopenick
- rosemary
- Steliosgkougkou
- the purge
- AnnaRd
- Signor Positivo
- onion
- cinnamongirl
- mister
- thenutritionist
- angies
- sophia<3
- Peter Pan13
- angeloskar
- Georgek7
- tapeinoxamomilaki
- Ιωάννης1234
- Praxis
- Mariahj
- Τρελας123
- Sherlockina
- Παναρας
- DimitrisGk
- Ελεν
- giannhs2001
- Idontknoww
- anakiriak@yahoo
- mpapa
- BlackBetty97
- ager
- kost28
- Eirinakiii8
- Cat lady
- Marple
- χημεια4λαιφ
- Apocalypse
- Valeris
- Vask
- Ioanna98
- ougka pougka
- GeorgePap2003
- Johanna Mark
- bruh_234
- augustine
- alpha.kappa
- Hermione granger
- constansn
- emilyfan85
- 2005
- George.S
- Dion G.
- SlimShady
- Corn90
- Meow
- Phys39
- Nick0007
- Nikoletaant
- Ameliak
- beckyy
- Rina
- Athens2002
- Eleni:
- Specon
- elenaaa
- Αντικειμενικός
- Mariaathens
- panosveki
- Superhuman
- GStef
- Gewrgia!
- papa2g
- Σωτηρία
- antonis97
- Georgekk
- Theodora03
- vetas
- _Aggelos123
- Κώστας 7708
- Alexandros973
- Cortes
- Katerinaki13
- Jimmy20
- igeorgeoikonomo
- KaterinaL
- thecrazycretan
- alexandra_
- StavMed
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

