Civilara
Περιβόητο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Α Θεωρώ
Η f είναι συνεχής στο
Ομοίως αν
Αν
Άρα για κάθε
B. Μία συνάρτηση f λέγεται παραγωγίσιμη σε ένα σημείο
και είναι πραγματικός αριθμός. Τότε η τιμή αυτού του ορίου λέγεται παράγωγος της f στο
Γ. α) Σωστό, β) Σωστό, γ) Λάθος, δ) Λάθος, ε) Λάθος
ΘΕΜΑ 2ο
Α. α) z=x+iy όπου
Έχουμε
β)
Όταν το μέτρο του z γίνεται ελάχιστο, ελαχιστοποιείται και το τετράγωνό του.
Θέτω
f συνεχής στο
f συνεχής στο
Άρα η f παρουσιάζει ολικό ελάχιστο στο
Άρα ο μιγαδικός
Ο
Β.
Πρέπει
Άρα
-----------------------------------------
ΘΕΜΑ 1ο
Α Θεωρώμε
Η f είναι συνεχής στοκαι παραγωγίσιμη στο
. Οπότε σύμφωνα με το θεώρημα μέσης τιμής διαφορικού λογισμού, υπάρχει
, τέτοιο ώστε
Ομοίως αν. Άρα για κάθε {x}_{1}, {x}_{2}in Delta ισχύει
που σημαίνει ότι η f είναι σταθερή σε όλο το Δ.
B. Μία συνάρτηση f λέγεται παραγωγίσιμη σε ένα σημείοτου πεδίου ορισμού της, εφόσον υπάρχει το όριο
και είναι πραγματικός αριθμός. Τότε η τιμή αυτού του ορίου λέγεται παράγωγος της f στοκαι συμβολίζεται με:
Γ. α) Σωστό, β) Σωστό, γ) Λάθος, δ) Λάθος, ε) Λάθος
ΘΕΜΑ 2ο
Α. α) z=x+iy όπουκαι
Έχουμε
β)
Όταν το μέτρο του z γίνεται ελάχιστο, ελαχιστοποιείται και το τετράγωνό του.
Θέτω. Η f είναι συνεχής και παραγωγίσιμη στο R ως πολυωνυμική με παράγωγο
f συνεχής στο, f παραγωγίσιμη στο
και
για κάθε x στο
. Άρα η f είναι γνησίως φθίνουσα στο
.
f συνεχής στο, f παραγωγίσιμη στο
και
για κάθε x στο
. Άρα η f είναι γνησίως αύξουσα στο
.
Άρα η f παρουσιάζει ολικό ελάχιστο στοτο οποίο έχει τιμή
Άρα ο μιγαδικόςέχει το μικρότερο δυνατό μέτρο από τους μιγαδικούς του προηγούμενου ερωτήματος και έχει μέτρο
Οαντιστοιχεί σε τιμή του λ,
Β.
Πρέπεικαι
Άρα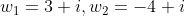
ΘΕΜΑ 3ο
A.
Άρα
Το πεδίο ορισμού της f είναι το
Η f είναι ορισμένη στο Α, παραγωγίσιμη στο
Άρα
B. α)
f συνεχής και παραγωγίσιμη στο Α με
Η f΄ είναι παραγωγίσιμη στο Α. Άρα η f είναι 2 φορές παραγωγίσιμη στο Α με δεύτερη παράγωγο:
Το εσωετρικό του Α ταυτίζεται με το Α καθώς το Α είναι ανοικτό διάστημα.
Η f είναι συνεχής στο Α και 2 φορές παραγωγίσιμη στο εσωτερικό του Α και ισχύει
β) f κυρτή στο Α => f΄ γνησίως αύξουσα στο Α
f΄(0)=0
Η f είναι συνεχής στο (-1,0], παραγωγίσιμη στο (-1,0) και ισχύει f΄(x)<0 για κάθε x στο (-1,0). Άρα η f είναι γνησίως φθίνουσα στο (-1,0]
H f είναι συνεχής στο
γ) f(0)=1
Η f είναι γνησίως φθίνουσα στο (-1,0], οπότε
Η f είναι γνησίως αύξουσα στο
Επομένως για κάθε
Θεωρώ την συνάρτηση
Η g είναι συνεχής στο R ως πολυωνυμική.
Η g είναι συνεχής στο [1, 2] και ισχύει g(1)g(2)<0. Επομένως σύμφωνα με το θεώρημα Bolzano, υπάρχει τουλάχιστον ένα ξ στο (1,2) τέτοιο ώστε g(ξ)=0
Άρα η εξίσωση
έχει τουλάχιστον μία ρίζα στο (1,2).
ΘΕΜΑ 4ο
α. Επειδή η f είναι συνεχής στο [0,2], τότε η συνάρτηση
Επειδή η f είναι συνεχής στο [0,2], τότε η συνάρτηση h(x)=xf(x) είναι συνεχής στο [0,2]. Επειδή η h είναι συνεχής στο [0,2] τότε η συνάρτηση
είναι παραγωγίσιμη στο [0,2] και ισχύει
για κάθε x στο [0,2].
Ως συνεχείς συναρτήσεις στο [0,2], οι f,F,h,H είναι συνεχείς στο (0,2].
Συνεπώς η G στο (0,2] γράφεται
Άρα η G είναι συνεχής στο (0,2], αφού προκύπτει από πράξεις μεταξύ συνεχών συνατήσεων στο (0,2]
Θα υπολογιστεί το όριο
Επειδή
το όριο οδηγεί σε απροσδιόριστη μορφή 0/0. Έχουμε
Επομένως
Η συνάρτηση H είναι παραγωγίσιμη στο [0,2], οπότε είναι παραγωγίσιμη (από δεξιά-από μεγαλύτερες τιμές) στο 0.
Άρα από τον ορισμό της παραγώγου έχουμε:
F συνεχής στο [0,2] => F συνεχής (από δεξιά) στο 0 =>
Έχουμε
Άρα
που σημαίνει ότι η G είναι συνεχής (από δεξιά) στο 0.
Η G είναι συνεχής στο (0,2] και ισχύει
Επομένως η G είναι συνεχής στο [0,2].
β. Για x στο (0,2) είναι
Οι H και F είναι παραγωγίσιμες στο [0,2], οπότε και στο (0,2).
Η συνάρτηση
Επομένως η
είναι παραγωγίσιμη στο (0,2) και έχει παράγωγο:
Άρα
για κάθε x στο (0,2)
γ.
G συνεχής στο [0,2], G παραγωγίσιμη στο (0,2) και G(0)=G(2). Επομένως σύμφωνα με το θεώρημα Rolle, υπάρχει τουλάχιστον ένα α στο (0,2) τέτοιο ώστε
δ.
G συνεχής στο [0,α] και G παραγωγίσιμη στο (0,α). Επομένως σύμφωνα με το θεώρημα μέσης τιμής του διαφορικού λογισμού υπάρχει τουλάχιστον ένα ξ στο (0,α) τέτοιο ώστε
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
m3Lt3D
Πολύ δραστήριο μέλος


Ουτε εγω την εγραψα γιατι ειναι πληρως τεκμηριωμενη χωρις να γραψεις αυτο το χαζο σχολιο που γραφει το σχολικο που πιστευω πως ειναι περισσοτερο για διδακτικο σκοπο.
Πιστευω ομως πως θα χασω για αυτο λιγα μορια.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Παρεπιπτόντως, εκείνη η ασκησούλα στο topic "καλή άσκηση" ήταν super.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Stefi17
Νεοφερμένο μέλος


Έλα τώρα ρε Γιάννη. Είπαμε να είμαστε αναλυτικοί, όχι κι έτσι. Γι αυτήν την χαζομάρα δεν θα χάσεις ούτε μισό μόριο. Αυτό είναι ταυτότητα και ισχύειο για ΟΛΕΣ τις συναρτήσεις, όχι μόνο για την σταθερή. Αφού ισχύει για όλες θα ισχύει και για την σταθερή. Μην ασχολούμαστε με μ******ς τώρα.
Παρεπιπτόντως, εκείνη η ασκησούλα στο topic "καλή άσκηση" ήταν super.
Αχχ,χάλιααααααααα τα πήγα..10 με το ζόρι,είχα πολύ άγχος και δεν μπορούσα να συγκεντρωθώ,βέβαια γενικά δυσκολεύομαι στα μαθηματικά,τώρα ό,τι έγινε,εγινε..

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
m3Lt3D
Πολύ δραστήριο μέλος


 .
.Ευχαριστω εννοειται πως δεν ειναι δικια μου.

Τα Σ/Λ απο που τα αντλουσες; Ηταν παρα πολυ καλα, αν και πολλα απο αυτα ξεφευγαν απο τα πλαισια του μαθηματος. (πχ αυτο που για να το καταριψεις επρεπε να ξερεις την συναρτηση weierstrass.)
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Όχι, ε; Κι όμως, είναι αλήθεια. Είναι δικιάς μου έμπνευσης.
Είμαι ένας πολιτικός μηχανικός κολλημένος με τα μαθηματικά και κάθε χρονιά λύνω τα θέματα των πανελληνίων(εγώ έδωσα πανελλήνιες στην Γ Λυκείου το 2002-άσχετο αλλά το πετάω). Μέχρι στιγμής δεν έχει περάσει χρονιά που να μην τα λύσω.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
m3Lt3D
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
billdef
Νεοφερμένο μέλος


κ.ο.κ.
ειναι σωστη αυτη η λογικη???
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


καλησπερα,τα εγραψα ολα τελεια....αλλα στο θεμα 3,β ερωτημα μαλλον εκανα πατατα....ειπα το εξης...f'(x)>o<=>e^x(x+1)>1 και επειδη e^x<=>0 τοτε χ>0
κ.ο.κ.
ειναι σωστη αυτη η λογικη???
Από ότι κατάλαβα έκανες το εξής. Λες πολύ σωστά ότι (e^x)*(x+1)>1 για x>-1. Μέχρι εδώ καλά. Μετά λες ότι επειδή e^x>0 τότε για να ισχύει η ανισότητα πρέπει x+1>1<=>x>0? Αυτό είναι λάθος γιατί αν πολλαπλασιάσεις με το (e^(-x))>0 για κάθε x τότε προκύπτει x+1>e^(-x) για κάθε x>-1 και όχι x+1>1. Όμως δεν ισχύει e^(-x)>1 για κάθε x>-1, έτσι δεν είναι; e^(-x)>1 για -1<x<0. Άρα η λογική σου είναι λανθασμένη.
-----------------------------------------
Σε γενικές γραμμές τα θέματα ήταν μέτριας δυσκολίας με σταδιακή κλιμάκωση του επιπέδου δυσκολίας όπως έπρεπε να είναι. Απευθύνονται σε καλά προετοιμασμένους υποψηφίους, αλλά δεν ξεχωρίζει ο καλός από τον πολύ καλό και ο πολύ καλός από τον άριστο.
Τα ερωτήματα 3Βγ,4γ και 4δ που ήταν αυξημένης δυσκολίας πιάνουν συνολικά 20/100 μονάδες, δηλαδή 4/20. Κατά συνέπεια ένας καλα διαβασμένος μπορεί να πιάσει το 16/20. Από εκεί και πέρα η δυσκολία αυξανόταν όμως δεν απαιτούσε συνθετική κρίση καθώς ήταν καθαρή εφαρμογή των θεωρημάτων.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
billdef
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
variax
Νεοφερμένο μέλος


Έλα τώρα ρε Γιάννη. Είπαμε να είμαστε αναλυτικοί, όχι κι έτσι. Γι αυτήν την χαζομάρα δεν θα χάσεις ούτε μισό μόριο. Αυτό είναι ταυτότητα και ισχύειο για ΟΛΕΣ τις συναρτήσεις, όχι μόνο για την σταθερή. Αφού ισχύει για όλες θα ισχύει και για την σταθερή. Μην ασχολούμαστε με μ******ς τώρα.
Παρεπιπτόντως, εκείνη η ασκησούλα στο topic "καλή άσκηση" ήταν super.
Δυστυχώς στο βαθμολογικό κέντρο που εξετάζω φυσικώς αδυνάτους η οδηγία σήμερα ήταν να κοπούν 2 μόρια στην περίπτωση που δεν εξεταστεί το x1=x2.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
m3Lt3D
Πολύ δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
smallv17
Νεοφερμένο μέλος


Στην ερωτηση για το ποια ειναι η ευθεια στην οποια ανηκουν οι εικονες των μιγαδικων επειδη ελεγε οτι ισχυει για οποιοδηποτε λεR εβαλα 2 τυχαιες τιμε στο λ εστω 0 και 1 βρηκα 2 σημεια, μετα το συντελεστη διευθυνσης της ευθεια που τα ενωνει και υστερα βρηκα την ευθεια. ειναι λαθος?
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
markou
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DK1991
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
miv
Επιφανές μέλος


Γεια σε ολους, θα ηθελα να κανω μια ερωτηση για το δευτερο θεμα που με απασχολει τωρα που κοιταξα τισ λυσεις στο διαδικτυο.
Στην ερωτηση για το ποια ειναι η ευθεια στην οποια ανηκουν οι εικονες των μιγαδικων επειδη ελεγε οτι ισχυει για οποιοδηποτε λεR εβαλα 2 τυχαιες τιμε στο λ εστω 0 και 1 βρηκα 2 σημεια, μετα το συντελεστη διευθυνσης της ευθεια που τα ενωνει και υστερα βρηκα την ευθεια. ειναι λαθος?
Δεδομένου ότι η εκφώνηση ζητάει ευθεία και όχι γενικά γεωμετρικό τόπο, νομίζω ότι δεν θα θεωρηθεί εντελώς λάθος.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Γεια σε ολους, θα ηθελα να κανω μια ερωτηση για το δευτερο θεμα που με απασχολει τωρα που κοιταξα τισ λυσεις στο διαδικτυο.
Στην ερωτηση για το ποια ειναι η ευθεια στην οποια ανηκουν οι εικονες των μιγαδικων επειδη ελεγε οτι ισχυει για οποιοδηποτε λεR εβαλα 2 τυχαιες τιμε στο λ εστω 0 και 1 βρηκα 2 σημεια, μετα το συντελεστη διευθυνσης της ευθεια που τα ενωνει και υστερα βρηκα την ευθεια. ειναι λαθος?
Αν έκανες μόνο αυτό δεν είναι λάθος άλλα είναι ελλιπές. Βάζεις 2 τυχαίες τιμές στο λ, βρίσκεις 2 σημεία και στη συνέχεια την εξίσωση της ευθείας που διέρχεται από αυτά τα δύο σημεία. Έχεις αποδείξει ότι η ευθεία αυτή διέρχεται για 2 συγκεκριμένες τιμές του λ και όχι για κάθε λ στο R. Μετά αντικαθιστάς στην εξίσωση που βρήκες x=2λ+1 και y=2λ-1 και πρέπει η εξίσωση να επαληθευτεί για οποιοδήποτε λ στο R. Τότε θα ήταν ολόσωστο. Αν μετά στην εξίσωση που βρήκες από τα 2 σημεία δεν την επαλήθευσες για κάθε λ τότε η απάντησή σου είναι ελλιπής.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
smallv17
Νεοφερμένο μέλος


Δεδομένου ότι η εκφώνηση ζητάει ευθεία και όχι γενικά γεωμετρικό τόπο, νομίζω ότι δεν θα θεωρηθεί εντελώς λάθος.
Λες ε?
Aπλα επειδη ζηταει ''να βρειτε την εξισωση της ευθειας'' σκεφτηκα οτι αφου ισχυει για ολα τα λ τοτε οποια τιμη του λ κι αν βαλω θα την επαληθευει. Αλλα διαφερει απο τισ λυσεις που παρουσιαστηκαν στο διαδικτυο δεν σκεφτηκα κι εγω να το παω με τον κλασσικο τροπο.

-----------------------------------------
Αν έκανες μόνο αυτό δεν είναι λάθος άλλα είναι ελλιπές. Βάζεις 2 τυχαίες τιμές στο λ, βρίσκεις 2 σημεία και στη συνέχεια την εξίσωση της ευθείας που διέρχεται από αυτά τα δύο σημεία. Έχεις αποδείξει ότι η ευθεία αυτή διέρχεται για 2 συγκεκριμένες τιμές του λ και όχι για κάθε λ στο R. Μετά αντικαθιστάς στην εξίσωση που βρήκες x=2λ+1 και y=2λ-1 και πρέπει η εξίσωση να επαληθευτεί για οποιοδήποτε λ στο R. Τότε θα ήταν ολόσωστο. Αν μετά στην εξίσωση που βρήκες από τα 2 σημεία δεν την επαλήθευσες για κάθε λ τότε η απάντησή σου είναι ελλιπής.
Thanks ευχαριστω πολυ καταλαβα τι λες. Ποσο να χασω απο αυτο? Τα μισα?κριμα επιανε και 9..
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

