Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

manos66 · 16-03-09

Το Α ερώτημα απαντήθηκε παραπάνω

Β.i.
Έστω συνάρτηση f με
$\\ f (x) = 2x^2-2x+1, x \in R \\ f'(x) = 4x - 2 \\ f''(x) = 4 > 0 \\ f'(1) = f (0) + f (1) = 2$
Η f παρουσιάζει ελάχιστο στο $x_0 = \frac{1}{2}$
Κάτι λείπει από το Βi ερώτημα.

Β.ii)
Θ.Μ.Τ. στο [0, 1] με την f
υπάρχει ξ στο (0 , 1) τέτοιο ώστε f΄(ξ) = f (1) - f (0)
Είναι f΄(ξ) < f΄(1) διότι η f΄ είναι γν. αύξουσα
f (1) - f (0) < f (1) + f (0)
f (0) > 0

B.iii)
Θεωρούμε συνάρτηση g, με g (x) = f΄(x) - f (1)
g συνεχής στο [ξ , 1]
g (ξ) = f΄(ξ) - f (1) = f (1) - f (0) - f (1) = - f (0) < 0
g (1) = f΄(1) - f (1) = f (1) + f (0) - f (1) = f (0) > 0
Θ. Βolzano
g΄(x) = f΄΄(x) > 0 , άρα g γν. αύξουσα
άρα μοναδική ρίζα

bobiras11 · 16-03-09

Παιδιά χίλια σόρρυ αλλά δεν θυμάμαι την ακριβή διατύπωση του Β.ι)
Αύριο θα βρω τη φωτό με τα θέματα και θα το διορθώσω.
-----------------------------------------

Αρχική Δημοσίευση από manos66:
$f (x) = 2x^2-2x+1, x in R$

Να ρωτήσω.. οπού που ακριβώς προέκυψε αυτή η f, ο τύπος της εννοώ, γιατί δεν το πολυκατάλαβα..

mostel · 17-03-09

Δεν έπεσα και απ' το φεγγάρι, αλλά δε μπορώ να πιστέψω ότι υπάρχει μαθητής που δε θα λύσει αυτή την άσκηση και θα περάσει πολυτεχνείο.....

manos66 · 17-03-09

Αρχική Δημοσίευση από bobiras11:
Παιδιά χίλια σόρρυ αλλά δεν θυμάμαι την ακριβή διατύπωση του Β.ι)
Αύριο θα βρω τη φωτό με τα θέματα και θα το διορθώσω.
-----------------------------------------
Να ρωτήσω.. οπού που ακριβώς προέκυψε αυτή η f, ο τύπος της εννοώ, γιατί δεν το πολυκατάλαβα..

Απλά σου έγραψα ένα αντιπαράδειγμα που ικανοποιεί τις υποθέσεις σου και δεν παρουσιάζει ακρότατο στο 0 ή το 1 που ζητάς.

bobiras11 · 17-03-09

Αρχική Δημοσίευση από mostel:
Δεν έπεσα και απ' το φεγγάρι, αλλά δε μπορώ να πιστέψω ότι υπάρχει μαθητής που δε θα λύσει αυτή την άσκηση και θα περάσει πολυτεχνείο.....

Γι' αυτό και γω δεν πάω πολυτεχνείο

αν και το βρίσκω τσιμπημένο το θέμα ακόμα και για το μαθητή του 18,19.

manos66 · 19-03-09

Για τις συναρτήσεις f , g ισχύουν :

f , g παραγωγίσιμες στο R
f΄(x + y) - g΄(x + y) = f΄(y) - g΄(y), για κάθε x , y πραγματικούς
f (0) = g (0)
f (1) = g (1) + 1

Ν' αποδειχθεί ότι :
α. f (x) = g (x) + x, για κάθε x πραγματικό
β. οι εφαπτόμενες των γραφικών παραστάσεων των f και g στα σημεία με κοινή τετμημένη, τέμνονται πάνω στον άξονα y΄y.

galois01 · 19-03-09

Αρχική Δημοσίευση από manos66:
Για τις συναρτήσεις f , g ισχύουν :

f , g παραγωγίσιμες στο R

f΄(x + y) - g΄(x + y) = f΄(y) - g΄(y), για κάθε x , y πραγματικούς

f (0) = g (0)

f (1) = g (1) + 1

Ν' αποδειχθεί ότι :
α. f (x) = g (x) + x, για κάθε x πραγματικό
β. οι εφαπτόμενες των γραφικών παραστάσεων των f και g στα σημεία με κοινή τετμημένη, τέμνονται πάνω στον άξονα y΄y.

(α) Θέτοντας y=0 παίρνουμε

$f'(x)-g'(x)=f'(0)-g'(0)$ επομένως

$f(x)=g(x)+(f'(0)-g'(o))x+c$ για κάθε $x\in{R}$

Θέτοντας στην τελευταία x=0 παίρνουμε c=0, επομένως $f(x)=g(x)+(f'(0)-g'(o))x$ για κάθε $x\in{R}$

Θέτοντας τώρα x=1 παίρνουμε $f'(0)-g'(o)=1$

Τελικά παίρνουμε $f(x)=g(x)+x$ $\forall\in{R}$

(β) Οι εφαπτομένες στα $Α(x_{0},f(x_{0}))$ και $B(x_{0},g(x_{0}))$ είναι

$y_{1}=f'(x_{0})x+f(x_{0})-f'(x_{0}))x_{0}$

$y_{2}=g'(x_{0})x+g(x_{0})-g'(x_{0}))x_{0}$

Λύνοντας την εξίσωση $y_{1}=y_{2}$ σε συνδιασμό με το (α) για x=x0 προκύπτει x=0

οπότε τελειώσαμε.

Κώστας

KONNOS · 19-03-09

Πολυ σωστα!!απλα μια διορθωσουλα στο παραπανω...Στο (α) ερωτημα εχεις καταληξει οτι f(x)=g(x)+1....Mια χαρα ειναι η διαδικασια σου απλα πρεπει να αποδειξεις οτι f(x)=g(x)+x...απλα αλλαξε το 1 και καν το x..

manos66 · 19-03-09

Αρχική Δημοσίευση από galois01:
(α) Θέτοντας y=0 παίρνουμε

$f'(x)-g'(x)=f'(0)-g'(0)$ επομένως

$f(x)=g(x)+(f'(0)-g'(o))x+c$ για κάθε $xin{R}$

Θέτοντας στην τελευταία x=0 παίρνουμε c=0, επομένως $f(x)=g(x)+(f'(0)-g'(o))x$ για κάθε $xin{R}$

Θέτοντας τώρα x=1 παίρνουμε $f'(0)-g'(o)=1$

Τελικά παίρνουμε $f(x)=g(x)+1$ $forallin{R}$

(β) Για να βρούμε που τέμνονται οι γραφ. παραστάσεις λύνουμε την εξίσωση $f(x)=g(x)$ η οποία έχει μοναδική λύση την x=0.

Επομένως οι γραφ. παραστάσεων στα (0,f(0)) και (ο,g(0)) είναι

$y=f'(0)x+f(0)$ και $y=g'(0)x+g(0)$

Λύνουμε την εξίσωση

$f'(0)x+f(0)=g'(0)x+g(0)$ η οποία έχει μοναδική λύση την x=0,αφού από το (α) έχουμε $f'(0)=g'(0)+1$ , οπότε τελειώσαμε.

Κώστας

Όμορφη η λύση σου στο α΄ ερώτημα.
Στο β δεν ζητάμε εφαπτομένη στο κοινό τους σημείο αλλά
οι εφαπτόμενες στα Α(x0 , f (x0)) και B (x0 , g (x0)) να τέμνονται στον y΄y

galois01 · 19-03-09

Αρχική Δημοσίευση από KONNOS:
Πολυ σωστα!!απλα μια διορθωσουλα στο παραπανω...Στο (α) ερωτημα εχεις καταληξει οτι f(x)=g(x)+1....Mια χαρα ειναι η διαδικασια σου απλα πρεπει να αποδειξεις οτι f(x)=g(x)+x...απλα αλλαξε το 1 και καν το x..

Ευχαριστώ για την παρατήρηση μόλις το διόρθώσα

Λάθος λόγω βιασύνης

@manos66:Μάνο τώρα διάβασα το μήνυμά σου αλλά δεν προλαβαίνω να γράψω τώρα τη λύση γιατί έχω έκθεση σε λίγο(μπλιαχ). Μόλις τελειώσω τα φροντιστήρια θα τη γράψω.

Κώστας

kvgreco · 19-03-09

Αρχική Δημοσίευση από manos66:
Για τις συναρτήσεις f , g ισχύουν :

f , g παραγωγίσιμες στο R

f΄(x + y) - g΄(x + y) = f΄(y) - g΄(y), για κάθε x , y πραγματικούς

f (0) = g (0)

f (1) = g (1) + 1

Ν' αποδειχθεί ότι :
α. f (x) = g (x) + x, για κάθε x πραγματικό

Πού είναι το λάθος?
[f(x+y)-g(x+y)]'= [f(y)-g(y)]' η ανεξάρτητη μεταβληθή ας θεωρηθεί η y.

f(x+y)-g(x+y)+ c = f(y)-g(y)

γιά χ=-y προκύπτει f(y)-g(y)=c που γιά y=0 δίνει c=0.

Άρα γιά κάθε x του R ισχύει f(x)=g(x)!!

manos66 · 19-03-09

Αρχική Δημοσίευση από kvgreco:
Πού είναι το λάθος?
[f(x+y)-g(x+y)]'= [f(y)-g(y)]' η ανεξάρτητη μεταβληθή ας θεωρηθεί η y.

f(x+y)-g(x+y)+ c = f(y)-g(y)

γιά χ=-y προκύπτει f(y)-g(y)=c που γιά y=0 δίνει c=0.

Άρα γιά κάθε x του R ισχύει f(x)=g(x)!!

Αν θεωρηθεί η y ανεξάρτητη μεταβληθή τότε προκύπτει

f(x+y)-g(x+y)+ c(x) = f(y)-g(y)

kvgreco · 19-03-09

Αρχική Δημοσίευση από manos66:
Αν θεωρηθεί η y ανεξάρτητη μεταβληθή τότε προκύπτει

f(x+y)-g(x+y)+ c(x) = f(y)-g(y)

Αφού οι συναρτήσεις έχουν ίσες παραγώγους,διαφέρουν κατά σταθερά c.Τί εννοείτε με c(x);
Όμως αν κατάλαβα καλά ενοείτε ότι θέτοντας άλλη τιμη του χ θα παρουμε άλλη σταθερά?

manos66 · 19-03-09

Aφού θεωρείς το y ανεξάρτητη μεταβλητή
η "σταθερά" c μπορεί να είναι μια συνάρτηση του x
Η παράγωγος του c (x) ως προς y είναι 0.

mitsos_312 · 19-03-09

Σωστός ο galois! Όλα τα λεφτά ήταν αυτές οι ασκήσεις!Κρίμα που πλεον δεν θυμάμαι σχεδόν τίποτα!!! Kαλή συνέχεια στην προσπάθεια παίδες!!!

riemann80 · 20-03-09

δηλαδη οταν λεμε σταθερα εννοουμε σταθερα ως προς τη μεταβλητη που ολοκληρωνουμε ή παραγωγιζουμε.και αυτο ακριβως θα πει σταθερα: σταθερα ως προς τη μεταβλητη!

manos66 · 20-03-09

Έστω ότι ισχύουν :

η συνάρτηση f είναι συνεχής στο R
$\\ F (x) = \int_{0}^{x}f (t) dt$
F (1) = 2

α) Να υπολογιστεί το $\int_{0}^{1}[x f (x) + F (x)] dx$

β) Ν' αποδειχθεί ότι για κάθε $x\in R$ , υπάρχει $\xi \in R$ τέτοιο ώστε $\int_{x}^{1}f (t) dx = (1 - x) f(\xi )$

γ) Αν $\int_{x}^{1}f (t) dt \geq 2 - 2x$ , για κάθε $x\in R$ , ν' αποδειχθεί ότι :
. i) f (0) = f (1) = 2
. ii) η f έχει ένα τουλάχιστον κρίσιμο σημείο.

δ) Ν' αποδειχθεί ότι $\int_{0}^{1}f^2(t) dt \geq 4$ .

Συγνώμη dt αντί dx στα γ,δ.
τα διόρθωσα

bobiras11 · 20-03-09

Αρχική Δημοσίευση από galois01:
...

Θέτοντας τώρα x=1 παίρνουμε $f'(0)-g'(o)=1$

Τελικά παίρνουμε $f(x)=g(x)+x$ $forallin{R}$

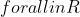
Εξήγησε το μία αυτό γιατί είμαι λίγο χαζός

Πως πήγες απ το πρώτο στο δεύτερο?

----------------------------
Άσε τώρα είδα τη σχέση από πάνω.
Η αϋπνία φταίει

kvgreco · 20-03-09

Αρχική Δημοσίευση από manos66:
Έστω ότι ισχύουν :

η συνάρτηση f είναι συνεχής στο R

$F (x) = int_{0}^{x}f (t) dt$

F (1) = 2

α) Να υπολογιστεί το $int_{0}^{1}[x f (x) + F (x)] dx$
β) Ν' αποδειχθεί ότι για κάθε $xin R$ , υπάρχει $xi in R$ τέτοιο ώστε $int_{x}^{1}f (t) dx = (1 - x) f(xi )$

γ) Αν $int_{x}^{1}f (t) dx geq 2 - 2x$ , για κάθε $xin R$ , ν' αποδειχθεί ότι :
. i) f (0) = f (1) = 2
. ii) η f έχει ένα τουλάχιστον κρίσιμο σημείο.

δ) Ν' αποδειχθεί ότι $int_{0}^{1}f^2(t) dx geq 4$ .

Γιά το α)
Το σπάμε και πολλαπλασιάζουμε το δεύτερο κομάτι με (x)' και μετά παραγοντική και φεύγει το $\int_{0}^{1}x f (x)dx$

Γιά το β) κάτι έχω διαβάσει γιά το θεώρημα μέσης τιμης του ολοκληρωτικου λογισμου αλλα αυτο το dx αν ήταν dt?
Γιά τα υπόλοιπα αφου φάμε πρώτα μεσημεριανο..

galois01 · 20-03-09

Αρχική Δημοσίευση από manos66:
Έστω ότι ισχύουν :

η συνάρτηση f είναι συνεχής στο R

$F (x) =int_{0}^{x}f(t) dt$

F (1) = 2

α) Να υπολογιστεί το $int_{0}^{1}[x f (x) + F (x)] dx$

β) Ν' αποδειχθεί ότι για κάθε $xin R$ , υπάρχει $xi in R$ τέτοιο ώστε $int_{x}^{1}f (t) dx = (1 - x) f(xi )$

γ) Αν $int_{x}^{1}f (t) dx geq 2 - 2x$ , για κάθε $xin R$ , ν' αποδειχθεί ότι :
. i) f (0) = f (1) = 2
. ii) η f έχει ένα τουλάχιστον κρίσιμο σημείο.

δ) Ν' αποδειχθεί ότι $int_{0}^{1}f^2(t) dxgeq 4$ .

(α) $\int_{0}^{1}[x f (x) + F (x)] dx=\int_{0}^{1}[xF'(x)+F(x)]=\int_{0}^{1}(xF(x))^{'}dx=2$

(β) Μήπως το dx που γράφεται είναι dt? Αν είναι έτσι τότε

Αν x=1 προφανώς ισχύει

Αν x>1 τότε από ΘΜΤ για την F στο [1,x] προκύπτει το ζητούμενο

Ομείως αν x<1

(γ)
Θέτουμε $g(x)=\int_{x}^{1}f (t) dx +2x-2$

i) Όμως από την υπόθεση $g(x)\geq0=g(1)=g(0)$ , $\forall x\in{R}$

Επομένως από το Θ. Fermat $g'(1)=g'(0)=0$ οπότε προκύπτει $f(0)=f(1)=2$

ii)Αν η f είναι παραγωγίσιμη στο (0,1) τότε η f ικανοποιεί τις υποθέσεις του θεωρήματος Rolle στο [0,1] επομένως η παραγωγος μηδενίζεται σε ένα τουλ, σημείο του (0,1) επομένως έχουμε ένα κρίσιμο σημείο.
Αν πάλι η f δεν είναι παραγωγίσιμη έστω και σε ένα σημείο στο R τότε έχουμε πάλι ένα κρίσιμο σημείο.
Σε κάθε περίπτωση επομένως η f έχει ένα τουλ. κρίσιμο σημειο.

(δ) Για κάθε $t\in[0,1]$ ισχύει

$(f(t)-2)^{2}\geq0$ επομένως

$\int_{0}^{1}(f(t)-2)^{2}\geq0$ και κάνοντας πράξεις

παίρνουμε το ζητούμενο

P.S Αν μπορεί κάποιος απο τους moderators να φτιάξει τη LATEX στην παράθεση

Κώστας

Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένος