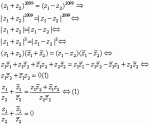vimaproto
Πολύ δραστήριο μέλος


α) Δεν καταλαβαίνω γιατί δίνει τη σχέση με τα μέτρα των μιγαδικών.στην ασκηση 1 σκεφτηκα αυτο :Code:[LATEX]{ \left| z-\overset { \_ }{ w } \right| }^{ 2 }={ \left| z+w \right| }^{ 2 }\\ \Longleftrightarrow (z-w)(\overset { \_ }{ z } -\overset { = }{ w } )=(z+w)(\overset { \_ }{ z } +\overset { \_ }{ w } )\\ \Longleftrightarrow z\overset { \_ }{ z } -zw-\overset { \_ }{ z } w+{ w }^{ 2 }=z\overset { \_ }{ z } +z\overset { \_ }{ w } +\overset { \_ }{ z } w+{ w }^{ 2 }\\ \Longleftrightarrow -zw-\overset { \_ }{ z } w=z\overset { \_ }{ w } +\overset { \_ }{ z } w\\ [/LATEX] αλλα μετα κολλησα και δεν ξερω πως να το συνεχισω.....καμια ιδεα:hmm: κανεις..??????
β) Ο συζυγής του συζυγούς είναι ο μιγαδικός. Αλλο ο w² και άλλο |w|²
Στη λύση τώρα
Z=x+yi και η σχέση που μας δίνει γράφεται: x+yi=-(x-yi) ==> x+yi=-x+yi ==> 2x=0 ==> x=0 Αρα Z=yi (φανταστικός)
Το αντίστροφο δηλ. Ζ=φανταστικός , να δειχτει η σχέση θα το κάνεις εσύ (πανεύκολο)
Η θεωρία λέει ότι όταν τριώνυμο 2ου βαθμού με πραγματικούς συντελεστές, έχει ρίζα μιγαδική, τότε έχει ως ρίζα και τη συζυγή της.
Αρα οι ρίζες του είναι χ1=-1+2ι και χ2=-1-2ι και ισχύει χ1+χ2=-(β/α)=-β άθροισμα ριζών ==> -1+2ι-1-2ι=-β ==> β=2
και αν θέλεις γινόμενο ριζών 2γ=(-1+2ι)(-1-2ι)=5 ==> γ=5/2
|Z-2Z1|=|Z2| ==> |x+yi-2+4i|=|3+4i| ==> |(x-2)+(y+4)|=|3+4i| ==> (x-2)²+y+4)²=3²+4²=25 Ο Γ.Τ. είναι κύκλος με κέντρο Κ(2,-4) και ακτίνα ρ=5
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος


Nα βρεθει το
[LATEX]\lim _{ x\rightarrow 1 }{ f\left( x \right) } [/LATEX]οταν:
1)[LATEX]\lim _{ x\rightarrow 1 }{ \frac { f\left( x \right) }{ { x }^{ 2 }+1 } } =-\infty [/LATEX]
2)[LATEX][\lim _{ x\rightarrow 1 }{ \frac { 2x-3 }{ f\left( x \right) } } =-\infty [/LATEX]
3)[LATEX]\lim _{ x\rightarrow 1 }{ \frac { { x }^{ 2 }-3 }{ f\left( x \right) } } =+\infty [/LATEX]Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
OChemist
Πολύ δραστήριο μέλος


Απλώς θέσε συναρτησεις.......και λύσε ως προς f(x).......και τα όρια θα πρόκυψουν!!!γεια σας και παλι!!!Μηπως θα μπορουσε κανεις να βοηθησει στα παρακατω ερωτηματα....
Nα βρεθει τοCode:[LATEX]\lim _{ x\rightarrow 1 }{ f\left( x \right) } [/LATEX]οταν: 1)[LATEX]\lim _{ x\rightarrow 1 }{ \frac { f\left( x \right) }{ { x }^{ 2 }+1 } } =-\infty [/LATEX] 2)[LATEX][\lim _{ x\rightarrow 1 }{ \frac { 2x-3 }{ f\left( x \right) } } =-\infty [/LATEX] 3)[LATEX]\lim _{ x\rightarrow 1 }{ \frac { { x }^{ 2 }-3 }{ f\left( x \right) } } =+\infty [/LATEX]
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


1
Α)Αν οι μιγαδικοι αριθμοι Ζ1,Ζ2,Ζ3 ειναι διαφορετικοι ανα δυο και ισχυει η ισοτητα
lz1-z2l(στο τετραγωνο)+lz2-z3l(στο τετραγωνο)=lz3-z1l(στο τετραγωνο)
να αποδειξετε οτι ενας τουλαχιστον ατο τους z1,z2,z3 δεν ειναι πραγματικος αριθμος
β)αν z1,z2 ΕC με lz1l(στο τετ.)+lz2l(στο τετ.)=lz1-z2l (στο τετ.) ν.δ.ο
1 αν z2 διαφ. απο το 0 ο αριθμος z1/z2 ειναι φανταστικος
2 lz1+z2l=lz1-z2l
2. εστω οι μιγαδικοι z1,z1 διαφ. απο το 0 για τους οποιους ισχυει
(z1+z2) (στην 2999) = (z1-z2)(στην 2999)
ν.δ.ο
1.z1/z2+z1/z2(συζηγης)=0
2 ο μιγαδικος z1/z2 ειναι φανταστικος
3.το τριγωνο που εχει κορυφες τις εικονες των μιγαδικων z1,z2 και την αρχη των αξονων ειναι ορθογωνιο
3.αν για τους μιγαδικους z1,z2,z3 ισχυει
z1(σtο τετ.)+z2(στο τετ.)+z3(στο τετ.)= z1z2+z2z3+z3z1
ν.δ.ο το τριγ. που εχει κορυφες τις εικονες z1,z2,z3 ειναι ισοπλευρο
δεν ξερει καποιος κατι για τις ασκησεις?
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DrHouse
Διάσημο μέλος


Καταρχην,|z1 - z2| = |z2 - z3| = |z3 - z1|=ισοπλευρο
Αρα...
z12 + z 2 + z 3 - z1z2 - z2z3 - z3z1 = 0 = z12 + z 2 + z 3 = z1z2 + z2z3 + z3z1 ⇔ z12 + z 2 - z1z2 - z2z3 - z3z1 + z 3 = 0 ⇔
⇔ z12 + z 22 - 2z1z2 = z2z3 + z3z1 - z1z2 - z 32 = 0 ⇔ (z1 - z2)2 = z3 ⋅ (z2 - z3) + z1(z3 - z2) ⇔ (z1 -
z2)2 = (z3 - z1) ⋅ (z2 - z3) ⇔ (z1 - z2)3 = (z3 - z1) ⋅ (z2 - z3) ⋅ (z1 - z2) ⇔ |(z1 - z2)3| = |z3 + z1| ⋅
|z2 - z3| ⋅ |z1 - z2| ⇔ |z1 - z3| = 3 |z1 - z 2 | ⋅ |z 2 - z 3 | ⋅ |z 3 - z1| = Αoμοίως |z2 - z3| = |z3 - z1| = Α
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Ironboy
Δραστήριο μέλος


εχω 3 ασκησεις και θα ηθελα να με βοηθησετε να τις λυσω
1
Α)Αν οι μιγαδικοι αριθμοι Ζ1,Ζ2,Ζ3 ειναι διαφορετικοι ανα δυο και ισχυει η ισοτητα
lz1-z2l(στο τετραγωνο)+lz2-z3l(στο τετραγωνο)=lz3-z1l(στο τετραγωνο)
να αποδειξετε οτι ενας τουλαχιστον ατο τους z1,z2,z3 δεν ειναι πραγματικος αριθμος
β)αν z1,z2 ΕC με lz1l(στο τετ.)+lz2l(στο τετ.)=lz1-z2l (στο τετ.) ν.δ.ο
1 αν z2 διαφ. απο το 0 ο αριθμος z1/z2 ειναι φανταστικος
2 lz1+z2l=lz1-z2l
2. εστω οι μιγαδικοι z1,z1 διαφ. απο το 0 για τους οποιους ισχυει
(z1+z2) (στην 2999) = (z1-z2)(στην 2999)
ν.δ.ο
1.z1/z2+z1/z2(συζηγης)=0
2 ο μιγαδικος z1/z2 ειναι φανταστικος
3.το τριγωνο που εχει κορυφες τις εικονες των μιγαδικων z1,z2 και την αρχη των αξονων ειναι ορθογωνιο
3.αν για τους μιγαδικους z1,z2,z3 ισχυει
z1(σtο τετ.)+z2(στο τετ.)+z3(στο τετ.)= z1z2+z2z3+z3z1
ν.δ.ο το τριγ. που εχει κορυφες τις εικονες z1,z2,z3 ειναι ισοπλευρο
δεν ξερει καποιος κατι για τις ασκησεις?
Εχω για την 2η ασκηση μια απάντηση
Λοιπον εχουμε και λεμε
Περνάμε μέτρα και προκύπτει ότι:
Άρα προκύπτει οτι
Υψωνουμε στο τετραγωνο κανουμε ιδιοτητες μετρων και προκυπτει οτι:
(Συζυγης) (Συζυγης)
Αρα κανεις πραξεις σε αυτο π σ ζηταει και θα δεις οτι αμα κανεις τις πραξεις στα κλασματα ο αριθμητης βγαινει η σχεση (1) αρα κανει 0
[/latex]
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


Χμμμ,για την τριτη εχω μια λυση-->
Καταρχην,|z1 - z2| = |z2 - z3| = |z3 - z1|=ισοπλευρο
Αρα...
z12 + z 2 + z 3 - z1z2 - z2z3 - z3z1 = 0 = z12 + z 2 + z 3 = z1z2 + z2z3 + z3z1 ⇔ z12 + z 2 - z1z2 - z2z3 - z3z1 + z 3 = 0 ⇔
⇔ z12 + z 22 - 2z1z2 = z2z3 + z3z1 - z1z2 - z 32 = 0 ⇔ (z1 - z2)2 = z3 ⋅ (z2 - z3) + z1(z3 - z2) ⇔ (z1 -
z2)2 = (z3 - z1) ⋅ (z2 - z3) ⇔ (z1 - z2)3 = (z3 - z1) ⋅ (z2 - z3) ⋅ (z1 - z2) ⇔ |(z1 - z2)3| = |z3 + z1| ⋅
|z2 - z3| ⋅ |z1 - z2| ⇔ |z1 - z3| = 3 |z1 - z 2 | ⋅ |z 2 - z 3 | ⋅ |z 3 - z1| = Αoμοίως |z2 - z3| = |z3 - z1| = Α
από πότε ξέρεις απο μαθηματικά εσύ;

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Ironboy
Δραστήριο μέλος
Aris90
Εκκολαπτόμενο μέλος


από πότε ξέρεις απο μαθηματικά εσύ;
τι εννοεις?

ευχαριστω για την λυση

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
eirini121
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


1 απορία.. α=β/(β^3+1)^1/2 πως λυνεις προς β??
Αν κατάλαβα καλά εννοείς ότι ο α=f(β) όπου f(x)=x/(((x^3)+1)^(1/2))
Η f έχει πεδίο ορισμού το A=(-1,+άπειρο)
Επίσης η f είναι συνεχής και παραγωγίσιμη στο Α με παράγωγο f΄(x)=(2-(x^3))/(2*(((x^3)+1)^(3/2)))
Η εξίσωση f΄(x)=0 έχει μοναδική ρίζα το x0=2^(1/3)
Η f είναι συνεχής στο (-1,2^(1/3)], παραγωγίσιμη στο (-1,2^(1/3)) και ισχύει f΄(x)>0 για x στο (-1,2^(1/3)). Επομένως η f είναι γνησίως αύξουσα στο διάστημα (-1,2^(1/3)].
Η f είναι συνεχής στο [2^(1/3),+άπειρο), παραγωγίσιμη στο (2^(1/3),+άπειρο) και ισχύει f΄(x)<0 για x στο (2^(1/3),+άπειρο). Επομένως η f είναι γνησίως φθίνουσα στο διάστημα [2^(1/3),+άπειρο).
Άρα η γραφική παράσταση της f παρουσιάζει ολικό μέγιστο στο x0 με τιμή f(2^(1/3))=(2^(1/3))/(3^(1/2))
Αν υπολογίσουμε τις οριακές τιμές της f προκύπτει ότι:
lim(x->-1+)f(x)=-άπειρο και lim(x->+άπειρο)f(x)=0. Επίσης ισχύει f(0)=0
Η f είναι συνεχής και γνησίως αύξουσα στο διάστημα (-1,2^(1/3)), συνεπώς f((-1,2^(1/3)))=(-άπειρο,(2^(1/3))/(3^(1/2)))
Η f είναι συνεχής και γνησίως φθίνουσα στο διάστημα (2^(1/3),+άπειρο), συνεπώς f((2^(1/3),+άπειρο))=(0,(2^(1/3))/(3^(1/2)))
Η f είναι συνεχής και γνησίως αύξουσα στο (-1,0) οπότε f((-1,0))=(-άπειρο,0)
Η f είναι συνεχής και γνησίως αύξουσα στο (0,2^(1/3)) οπότε f((0,2^(1/3)))=(0,(2^(1/3))/(3^(1/2)))
Συνεπώς
Για α<0 υπάρχει μοναδικό β με -1<β<0 ώστε α=f(β)
Για α>0 υπάρχουν β1, β2 με 0<β1<2^(1/3)<β2 τέτοια ώστε f(β1)=f(β2)=α
Για α=0 προκύπτει β=0 και αντίστροφα.
Συνεπώς για α>0 υπάρχουν δύο διαφορετικά β που δίνουν το ίδιο α.
Για α διάφορο του 0, υψώνουμε στο τετράγωνο και τα 2 μέλη οπότε προκύπτει:
α^2=(β^2)/((β^3)+1) => (α^2)*(β^3)-(β^2)+(α^2)=0
Εξετάζουμε περιπτώσεις ανάλογα αν α>0 ή α<0 και λύνουμε την τριτοβάθμια εξίσωση με βάση τον παρακάτω αλγόριθμο στο σύνδεσμο https://krieger.freehostia.com/cubic.htm
Δεν έχει καμία σχέση αυτή η άσκηση με τα μαθηματικά της Β΄ Λυκείου.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Δίνεται μια συνάρτηση f ορισμένη στο R, η οποία είναι γνησίως μονότονη και ισχύει η σχέση
Μήπως υπάρχει κάποιο λάθος στην άσκηση;

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χαρουλιτα
Διάσημο μέλος


Μπορει να κανω και λαθος βεβαια...
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Nikos Sitys
Πολύ δραστήριο μέλος


Σωστο εισαι χαρουλιλιλιλιλιλιλιλινιΕχει ριζα για x=2 η οποια μαλιστα ειναι μοναδικη αφου η f ειναι γνησιως μονοτονη!
Μπορει να κανω και λαθος βεβαια...
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Άσκηση 24/Μπάρλας σελ 112
Δίνεται μια συνάρτηση f ορισμένη στο R, η οποία είναι γνησίως μονότονη και ισχύει η σχέση, για κάθε
. Nα δείξετε ότι η εξίσωση f(x)=0 έχει μοναδική ρίζα.
Μήπως υπάρχει κάποιο λάθος στην άσκηση;
Για x=2 προκύπτει:
f(2)=-f(4-2) <=> f(2)=-f(2) <=> f(2)+f(2)=0 <=> 2f(2)=0 <=> f(2)=0
Η f είναι γνησίως μονότονη στο f οπότε είναι και 1-1. Συνεπώς:
f(x)=0 => f(x)=f(2) => x=2
Για x=2 προφανώς f(x)=f(2)=0
Άρα ισχύει η ισοδυναμία f(x)=0 <=> x=2
Η εξίσωση f(x)=2 έχει μοναδική λύση τη x=2.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Για x=2 προκύπτει:
f(2)=-f(4-2) <=> f(2)=-f(2) <=> f(2)+f(2)=0 <=> 2f(2)=0 <=> f(2)=0
Η f είναι γνησίως μονότονη στο f οπότε είναι και 1-1. Συνεπώς:
f(x)=0 => f(x)=f(2) => x=2
Για x=2 προφανώς f(x)=f(2)=0
Άρα ισχύει η ισοδυναμία f(x)=0 <=> x=2
Η εξίσωση f(x)=2 έχει μοναδική λύση τη x=2.
Ευχαριστώ!

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος


Δινονται οι συναρτησεις f , g : [LATEX]R\rightarrow R[/LATEX] για τις οποιες ισχυει:
[LATEX]\left( gof \right) \left( x \right) =2{ x }^{ 5 }+{ e }^{ f\left( x \right) }+1\quad[/LATEX] για καθε χ ε R.
Να δειξετε οτι η f ειναι 1-1.καμια ιδεα κανεις ???? εχω κολλησει ...και με μπερδευει η gof
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Βλα
Πολύ δραστήριο μέλος


Ασκηση 9 σελ 130 / Μπαρλας
Code:Δινονται οι συναρτησεις f , g : [LATEX]R\rightarrow R[/LATEX] για τις οποιες ισχυει: [LATEX]\left( gof \right) \left( x \right) =2{ x }^{ 5 }+{ e }^{ f\left( x \right) }+1\quad[/LATEX] για καθε χ ε R. Να δειξετε οτι η f ειναι 1-1.
καμια ιδεα κανεις ???? εχω κολλησει ...και με μπερδευει η gof
Έστω f(x1)=f(x2)
Τότε gof(x1)=gof(x2) => 2x1^5 +e^f(x1) +1 = 2x2^5 +e^f(x2) +1
Αφού από την υπόθεση f(x1)=f(x2) => e^f(x1)=e^f(x2)
Οπότε: 2x1^5=2x2^5 => x1^5=x2^5 , και επειδή ο εκθέτης είναι περιττός τον διώχνουμε και βγαίνει x1=x2
Άρα αποδείχθηκε.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
saktop
Νεοφερμένο μέλος


να δείξω ότι
. Όποιος μπορεί ας μου δώσει κάποιο tip και αν δεν μπορέσω μετά μου την λύνει.
f(f(x))= x^2 - x + 1 (1)
Hint: Στην (1) όπου χ το 1, f(f(1))=1 (2)
f(1) = f(1)^2 - f(1) + 1 <=> f(1)^2 - 2f(1) + 1 = 0 <=> (f(1) - 1)^2 = 0 <=> f(1) = 1
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 13 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki