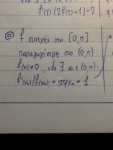Βοήθεια/Απορίες στα Μαθηματικά Προσανατολισμού - Ασκήσεις

[Guest 190013]

f '(x)/f(x) + σφx = 1
Θέλω να του κάνω αντιπαραγώγιση και να θέσω συνάρτηση για Rolle στο [0, π]. Καμιά βοήθεια;
--> Έφτιαξα την [ lnf(x) + ln(ημx) - x ]' = 0 αλλά δεν μπορώ να εφαρμόσω Rolle στο [0, π] για την g(x) = lnf(x) + ln(ημx) - x


edit: Τώρα είδα ότι είναι Β Λυκείου

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[DumeNuke]

f '(x)/f(x) + σφx = 1
Θέλω να του κάνω αντιπαραγώγιση και να θέσω συνάρτηση για Rolle στο [0, π]. Καμιά βοήθεια;
--> Έφτιαξα την [ lnf(x) + ln(ημx) - x ]' = 0 αλλά δεν μπορώ να εφαρμόσω Rolle στο [0, π] για την g(x) = lnf(x) + ln(ημx) - x


edit: Τώρα είδα ότι είναι Β Λυκείου

Ολόκληρη η εκφώνηση?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

Ολόκληρη η εκφώνηση?

την άσκηση μας την υπαγόρευσε, η περίπτωση λάθους στην εκφώνηση υπάρχει

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[eyb0ss]

την άσκηση μας την υπαγόρευσε, η περίπτωση λάθους στην εκφώνηση υπάρχει

Έστω με και (τρίκλαδη συνάρτηση).
διότι και
Αναλόγως βγαίνει ότι άρα g συνεχής στο , παραγωγίσιμη στο ,g(0)=g(π)=0, θεώρημα rolle και βγαίνει

cot(x)=σφx και sin(x)=ημx

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

Τρίκλαδη χαχα να σαι καλά ευχαριστώ

Edit: αλήθεια, από πού πήρες ότι g(0)=g(π)=0 ;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[eyb0ss]

Τρίκλαδη χαχα να σαι καλά ευχαριστώ

Edit: αλήθεια, από πού πήρες ότι g(0)=g(π)=0 ;;

Θεωρείς την συνάρτηση
(Αγνόησε τα <br/>) η οποία είναι συνεχής και παραγωγίσιμη στο
Την εξετάζουμε ως προς τη συνέχεια και τις τιμές στα άκρα 0,π και βγαίνει ότι , g συνεχής στο και g παραγωγίσιμη στο ,rolle και στη συνέχεια τρέχεις σε αυτόματο πιλότο.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

Άρα τα θέτουμε αυθαίρετα έτσι στην τρίκλαδη, δεν υπάρχει πρόβλημα με αυτό;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[eyb0ss]

Άρα τα θέτουμε αυθαίρετα έτσι στην τρίκλαδη, δεν υπάρχει πρόβλημα με αυτό;

Κανένα πρόβλημα απολύτως, το έχω δει και σε θέμα του ΟΕΦΕ.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

Good, thanks

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[DumeNuke]

Άρα τα θέτουμε αυθαίρετα έτσι στην τρίκλαδη, δεν υπάρχει πρόβλημα με αυτό;

Δεν το θέτεις έτσι αυθαίρετα, η εκφώνηση ορίζει ότι η συνάρτηση είναι συνεχής στο [0,π]. Άρα τα g(0) και g(π) ισούνται με τις αντίστοιχες οριακές τιμές της συνάρτησης.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

Δεν το θέτεις έτσι αυθαίρετα, η εκφώνηση ορίζει ότι η συνάρτηση είναι συνεχής στο [0,π]. Άρα τα g(0) και g(π) ισούνται με τις αντίστοιχες οριακές τιμές της συνάρτησης.

Η εκφώνηση ορίσει την f, όχι την g

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[eyb0ss]

https://panelladikes24.blogspot.gr/2013/05/2013_16.html
Προς klean: Κοίτα το ερώτημα Δ2 όπου εφαρμόζει Rolle σε δίκλαδη συνάρτηση (ΟΕΦΕ 2013). Η αλήθεια είναι ότι οι τιμές είναι αυθαίρετες επειδή εμείς τις ελέγχουμε αλλά αν θεωρούσαμε ότι πχ και τότε δεν θα φτάναμε ποτέ στη λύση. Καλά διαβάσματα και καλή επιτυχία!

Η εκφώνηση ορίσει την f, όχι την g

Αλλά με το θεώρημα Rolle το ζητούμενο θα βρίσκεται στο ανοιχτό διάστημα εκεί οπού ισχύει

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[DumeNuke]

nvm Πατάτα πέταξα...

Το πολύ τίτσου προκαλεί μόνιμη εγκεφαλική βλάβη... Να το προσέχετε!

Από μαθηματικής σκοπιάς, πάντως, δεν μπορούμε να αιτιολογήσουμε γιατί η συνάρτηση g πρέπει να είναι συνεχής στα άκρα του πεδίου... Σίγουρα, κανείς εξεταστής δεν θα έδινε βάση (το πιθανότερο είναι και οι ενδεικνυομενες λύσεις να το έδιναν έτσι), αλλά το κενό εξακολουθεί να υφίσταται...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

Πφφφ καλά πάω για ύπνο και αύριο με καθαρό μυαλό θα πάρω τηλ να βρίςω τον μαθηματικό σας ευχαριστώ για την βοήθεια παιδιά

Edit : DumeNuke κι εγώ εκεί κολλάω, στη βλάβη της γενικότητας

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

f '(x)/f(x) + σφx = 1
Θέλω να του κάνω αντιπαραγώγιση και να θέσω συνάρτηση για Rolle στο [0, π]. Καμιά βοήθεια;
--> Έφτιαξα την [ lnf(x) + ln(ημx) - x ]' = 0 αλλά δεν μπορώ να εφαρμόσω Rolle στο [0, π] για την g(x) = lnf(x) + ln(ημx) - x


edit: Τώρα είδα ότι είναι Β Λυκείου

g(x)=f(x)*(e^(-x))*ημx

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

g(x)=f(x)*(e^(-x))*ημx

Μπορείς να το βγάλεις αναλυτικά;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Μπορείς να το βγάλεις αναλυτικά;

[f΄(x)/f(x)]+σφx=1 => [f΄(x)/f(x)]+(συνx/ημx)=1 => f΄(x)ημx+f(x)συνx=f(x)ημx => (f(x)ημx)΄=f(x)ημx => (f(x)ημx)΄-f(x)ημx=0 =>
=> (f(x)ημx)΄(e^(-x))-f(x)ημx(e^(-x))=0 => (f(x)ημx)΄(e^(-x))+(f(x)ημx)(e^(-x))΄=0 => [f(x)ημx(e^(-x))]΄=0

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 190013]

Ωραίος, βγαίνει και κατευθείαν

Αν σου είναι εύκολο, δες και την προηγούμενη λύση και τον ΟΕΦΕ, ποια είναι η γνώμη σου;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[eyb0ss]

Ωραίος ο μηχανικός, πιο σύντομη λύση χωρίς όρια.
Edit: Και εμένα με δέρνει η βλακεία: Είναι

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Ωραίος, βγαίνει και κατευθείαν

Αν σου είναι εύκολο, δες και την προηγούμενη λύση και τον ΟΕΦΕ, ποια είναι η γνώμη σου;

Μπορεί να αποδειχθεί ότι υπάρχει το ξ χωρίς κλαδική συνάρτηση. Θεωρούμε τη συνάρτηση
h(x)=f(x)lnx+(F(x)/x)=F΄(x)lnx+(F(x)/x) με πεδίο ορισμού το (0,+οο).

Η f είναι παραγωγίσιμη στο [0,+οο) οπότε και συνεχής σε αυτό. Επομένως η F είναι δύο φορές παραγωγίσιμη στο [0,+οο) με
F΄(x)=f(x)
F΄΄(x)=f΄(x)
Είναι F(0)=0 και F΄(0)=f(0)=1

Από προηγούμενα ερωτήματα έχει προκύψει ότι F(x)>0 και F΄(x)>1>0 για x>0.

Για x=1 προκύπτει h(1)=F(1)>0

H f είναι συνεχής στο [0,+οο), οπότε είναι συνεχής στο 0 και επομένως lim(x->0+)f(x)=f(0)=1>0
Η συνάρτηση F είναι παραγωγίσιμη στο [0,+οο), οπότε είναι παραγωγίσιμη στο 0 με F΄(0)=f(0)=1
Από τον ορισμό της παραγώγου σε σημείο έχουμε:
lim(x->0+){[F(x)-F(0)]/(x-0)}=F΄(0) => lim(x->0+)(F(x)/x)=1

Επειδή lim(x->0+)f(x)=f(0)=1>0 και lim(x->0+)lnx=-oo τότε lim(x->0+)[f(x)lnx]=-oo => lim(x->0+)[F΄(x)lnx]=-oo
Επειδή lim(x->0+)(F(x)/x)=1 και lim(x->0+)[F΄(x)lnx]=-oo τότε lim(x->0+)h(x)=-oo

Η h είναι συνεχής στο (0,1) και ισχύει lim(x->0+)h(x)=-oo τότε το διάστημα (lim(x->0+)h(x), h(1))=(-oo,h(1)) είναι υποσύνολο της εικόνας h((0,1)) του διαστήματος (0,1) (αν η h ήταν γνησίως αύξουσα στο (0,1) τότε θα θα ήταν η εικόνα του ακριβώς και το ζητούμενο ξ θα ήταν μοναδικό). Επειδή το 0 ανήκει στο διάστημα (-οο,h(1)), καθώς h(1)>0, τότε υπάρχει τουλάχιστον ένα ξ ώστε h(ξ)=0.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 9 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.