Marel
Νεοφερμένο μέλος
Η Marel αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 19 ετών και Φοιτήτρια του τμήματος Ψυχολογίας ΕΚΠΑ. Έχει γράψει 91 μηνύματα.

04-10-23

23:33
Η σύνθετη κίνηση ενός σώματος μπορεί να μελετηθεί ως το αποτέλεσμα της σύνθεσης μιας μεταφορικής και μιας κυκλικής κίνησης; Σωστό - Λάθος
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.983 μηνύματα.

04-10-23

23:43
αν εβαζες ολοκληρη την προταση οπου αναφερεται , ,θα βλεπαμε καλυτερα .Η στροφική κίνηση ενός στερεού σώματος είναι ίδια με την κυκλική κίνηση ενός στερεού σώματος;
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.425 μηνύματα.

05-10-23

00:19
Καλησπέρα .Η στροφική κίνηση ενός στερεού σώματος είναι ίδια με την κυκλική κίνηση ενός στερεού σώματος;
Το σχολικό αναφέρει πως :
1) Στη στροφική κίνηση το σώμα αλλάζει προσανατολισμό .
2) Στη μεταφορική κίνηση κάθε στιγμή όλα τα σημεία του σώματος έχουν την ίδια ταχύτητα .
3) Όταν ένα σώμα μετακινείται στο χώρο και ταυτόχρονα αλλάζει ο προσανατολισμός του λέμε ότι κάνει σύνθετη κίνηση.
Στην κυκλική κίνηση το στερεό μετακινείται στον χώρο αλλά δεν αλλάζει απαραίτητα προσανατολισμό .
Το σχολικό βιβλίο έχει ένα καλό παράδειγμα που αναφέρει οτι ο τροχός του λούνα παρκ κάνει στροφική κίνηση , αλλά οι θαλαμίσκοι κάνουν μεταφορική κίνηση .
Marel
Νεοφερμένο μέλος
Η Marel αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 19 ετών και Φοιτήτρια του τμήματος Ψυχολογίας ΕΚΠΑ. Έχει γράψει 91 μηνύματα.

05-10-23

00:22
Ευχαριστώ πολύ!
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

05-10-23

16:29
iiTzArismaltor_
Νεοφερμένο μέλος
Ο Άρης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής. Έχει γράψει 65 μηνύματα.

05-10-23

16:40
Γεια σου Marel. Για αρχή, καλό είναι να φτιάξεις στο τετράδιό σου ένα δικό σου σχήμα και να σημειώσεις τις δυνάμεις που ασκούνται (βάρος, τάση του νήματος, F και FA). Η τάση έχει διεύθυνση ίδια με το νήμα και φορά από τη ράβδο προς αυτό (δηλαδή προς τα αριστερά στη συγκεκριμένη άσκηση). Η FA είναι η δύναμη που ασκείται από την άρθρωση. Επειδή υπάρχουν δυνάμεις και στον κατακόρυφο (βάρος, F), αλλά και στον οριζόντιο άξονα (τάση την οποία ας ονομάσουμε Τν) και η ράβδος ισορροπεί, προκύπτει ότι η FA έχει τυχαία κατεύθυνση. Σε αυτήν την περίπτωση, μπορούμε να την αναλύσουμε σε 2 συνιστώσες.
Στη συνέχεια, αυτό που πρέπει να εφαρμόσουμε είναι τις συνθήκες ισορροπίας. Η ράβδος ισορροπεί και στροφικα, αλλά και μεταφορικά. Με άλλα λόγια, Στ = 0 και ΣF = 0. Η συνολική ροπή της ράβδου είναι 0 ως προς οποιοδήποτε σημείο. Ωστόσο, μας συμφέρει να την υπολογίσουμε ως προς το σημείο Α, όπου η άγνωστη δύναμη FA (άγνωστη κατεύθυνση & άγνωστο μέτρο) έχει μηδενική ροπή. Από το Στ = 0 θα βρούμε μια σχέση για το μέτρο της Τν. Ξέρουμε, επίσης, ότι ΣFy = 0 και ΣFx = 0. Όμως, από πυθαγόρειο ισχύει και FAy² + FAx² = FA². Συνδιάζοντας όλες τις σχέσεις θα καταλήξεις στο ζητούμενο αποτέλεσμα. Δε θα στείλω κάτι παραπάνω από τώρα, γιατί καλό είναι να προσπαθήσεις κι εσύ λίγο παραπάνω την άσκηση τώρα που πήρες λίγη βοήθεια.
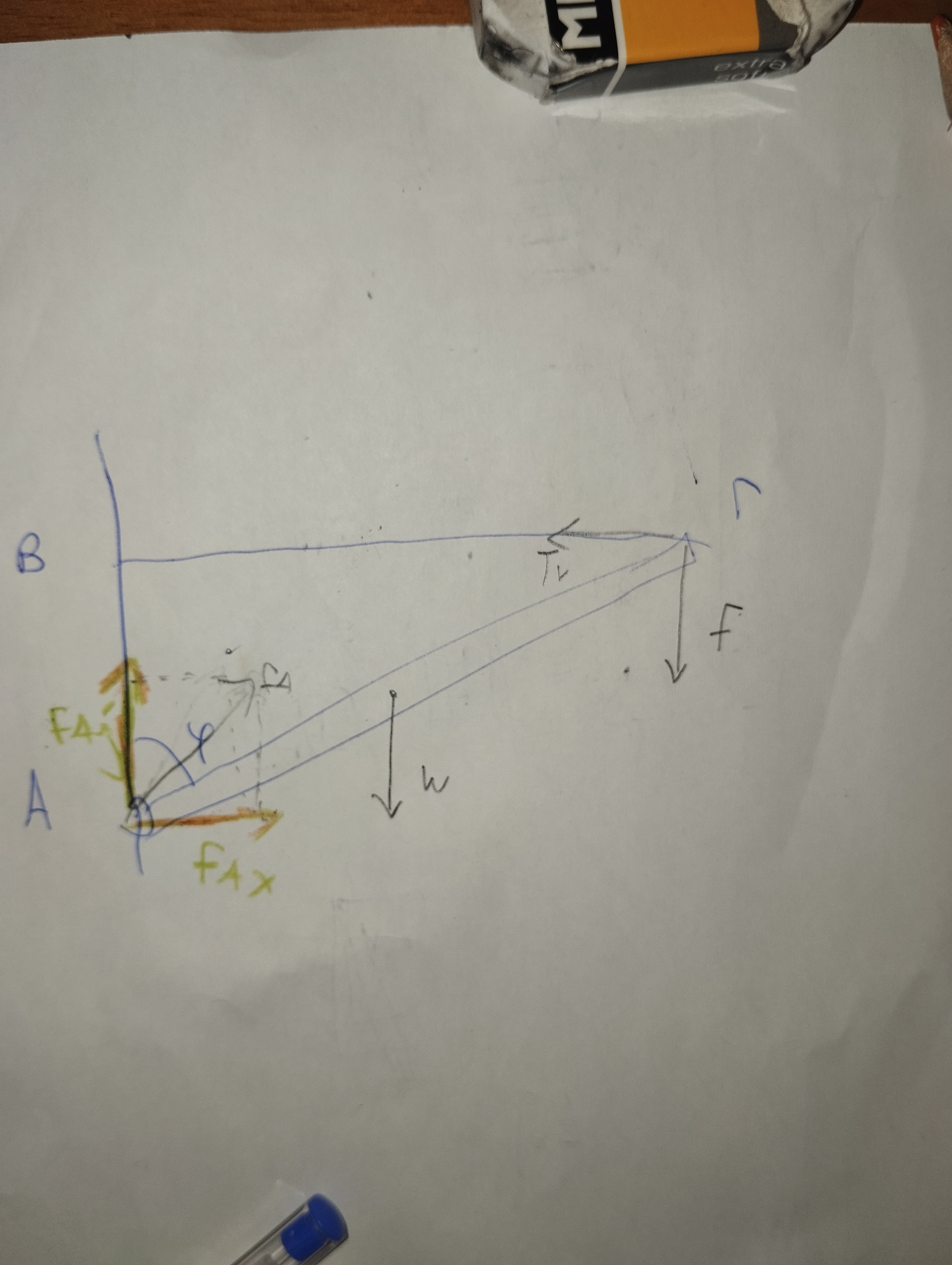
Στη συνέχεια, αυτό που πρέπει να εφαρμόσουμε είναι τις συνθήκες ισορροπίας. Η ράβδος ισορροπεί και στροφικα, αλλά και μεταφορικά. Με άλλα λόγια, Στ = 0 και ΣF = 0. Η συνολική ροπή της ράβδου είναι 0 ως προς οποιοδήποτε σημείο. Ωστόσο, μας συμφέρει να την υπολογίσουμε ως προς το σημείο Α, όπου η άγνωστη δύναμη FA (άγνωστη κατεύθυνση & άγνωστο μέτρο) έχει μηδενική ροπή. Από το Στ = 0 θα βρούμε μια σχέση για το μέτρο της Τν. Ξέρουμε, επίσης, ότι ΣFy = 0 και ΣFx = 0. Όμως, από πυθαγόρειο ισχύει και FAy² + FAx² = FA². Συνδιάζοντας όλες τις σχέσεις θα καταλήξεις στο ζητούμενο αποτέλεσμα. Δε θα στείλω κάτι παραπάνω από τώρα, γιατί καλό είναι να προσπαθήσεις κι εσύ λίγο παραπάνω την άσκηση τώρα που πήρες λίγη βοήθεια.
Marel
Νεοφερμένο μέλος
Η Marel αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 19 ετών και Φοιτήτρια του τμήματος Ψυχολογίας ΕΚΠΑ. Έχει γράψει 91 μηνύματα.

05-10-23

17:41
Ευχαριστώ πολύ!
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Ευχαριστώ πολύ!
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.983 μηνύματα.

05-10-23

21:02
Μια πολυ εξυπνη κλασσική ασκηση ... ευγε στο Δια και τον Αρη που την ελυσαν υποδειγματικα ,ευγε και σε εκεινο που την εβαλε..
Νωρις ομως δεν τα ζοριζουν τα παιδια? Αραγε τι πιο δυσκολο ελυσε ο δασκαλος στον πινακα?
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

05-10-23

22:11
Μπα!!! Αν αυτή σου φαίνεται δύσκολη, δες τι ανέβασα στο θέμα των ενδιαφέροντών προβλημάτων.Μια πολυ εξυπνη κλασσική ασκηση ...
Νωρις ομως δεν τα ζοριζουν τα παιδια? Αραγε τι πιο δυσκολο ελυσε ο δασκαλος στον πινακα?
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

10-10-23

00:18
Marel
Νεοφερμένο μέλος
Η Marel αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 19 ετών και Φοιτήτρια του τμήματος Ψυχολογίας ΕΚΠΑ. Έχει γράψει 91 μηνύματα.

10-10-23

00:31
Ευχαριστώ πολύ!
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

10-10-23

09:37
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

17-10-23

02:41
Ο εκθέτης σου δεν διαβάζεται και έβαλα δικό μου. Αν δεν είναι ίδιος, ο τρόπος ισχύει.
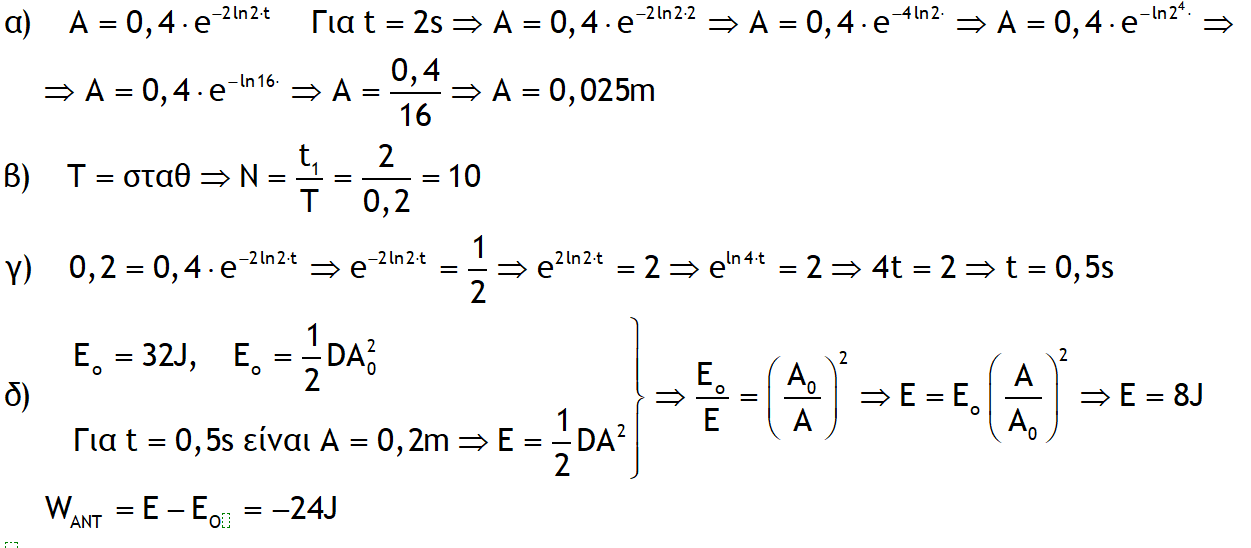
Δεν νυστάζεις;

Δεν νυστάζεις;
Marel
Νεοφερμένο μέλος
Η Marel αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 19 ετών και Φοιτήτρια του τμήματος Ψυχολογίας ΕΚΠΑ. Έχει γράψει 91 μηνύματα.

17-10-23

02:43
Δεν τα πάω καλά με τον ύπνο.
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

17-10-23

02:46
Κι εγώ αυπνίες έχω....

Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 159 μέλη διάβασαν αυτό το θέμα:
- Marel
- trifasikodiavasma
- Hased Babis
- Corfu kitty
- userguest
- suaimhneas
- Maynard
- Joji
- Reader
- jellojina
- Hecticism
- pnf292
- BatGuin
- panosT436
- sofia07
- patatosalata22
- Than003
- FNC_Sophia
- iren
- Giannis_19
- jYanniss
- wmaria
- Kate1914
- Viktoriaki
- Vasilis125
- Steliosgkougkou
- mysticfallsgirl12
- Lia 2006
- Ness
- ioanna2007
- donut_daddy
- ntinos...
- sciencegeek
- Unboxholics
- woasibe
- sophiaa
- GV221
- charmander
- bibliofagos
- Evangeloz
- bbb
- love_to_learn
- Panatha mono
- Enhypen
- despoina13
- panaman
- grad778
- Greg25
- thepigod762
- nikolakisss_
- Magigi
- peter347
- Alexecon1991
- synthnightingale
- Indecisive2
- Only physics
- Γατέχων
- Startx0
- Wonderkid
- Scandal
- flowermd
- Help :)
- Chrisphys
- Helen06
- Mitsaras23
- Marianna.diamanti
- Albert.123
- tan07
- phleidhs
- Georgepap_21
- Coconut201
- MrDragonboy
- chjan
- soleilst
- Ilovemycats27
- BiteTheDust
- Μήτσος10
- Elwik
- Mariahj
- DetectiveAgg
- stee
- nimbus
- Yorgos L
- bill09876
- marilenaaa
- pannnos1992
- fofo
- carnage
- Mhtsaras76
- user111
- Obi-Wan Kenobi
- neurogirl
- Lifelong Learner
- Yolo06
- ROULI
- Human being
- iiTzArismaltor_
- Chris180
- math2arch
- Εριφύλη
- Jimpower
- Χρήστος2006
- dimitra*
- xrisamikol
- xristarac
- gmoutzour
- Mara2004
- PanosApo
- eukleidhs1821
- angies
- AggelikiGr
- Sofos Gerontas
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

