OChemist
Πολύ δραστήριο μέλος


2ος ΤΡΟΠΟΣ
λοιπόν ισχύει
και άρα
άρα
όμως.....
οπότε η (1) γινεται


 ......Καλα ε....Μεσα στο μυαλό μου εισαι
......Καλα ε....Μεσα στο μυαλό μου εισαι
 ....Αυτο πηγα να γραψω!!!!!
....Αυτο πηγα να γραψω!!!!!




Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Αν οι πραγματικοί αριθμοί
να δείξετε ότι
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dimitris001
Τιμώμενο Μέλος


Λοιπόν απο τη στιγμή που εχουν απόλυτα μπορούμε να υψώσουμε στο τετράγωνο άραΑφου μαζευτηκαν και τα μπιγκ μποιζ ριχνω κατι αναλογο :
Αν οι πραγματικοί αριθμοίείναι τέτοιοι ώστε

να δείξετε ότι
με πρόσθεση των (1),(2) και (3) έχουμε:
άρα
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
OChemist
Πολύ δραστήριο μέλος


Λοιπόν απο τη στιγμή που εχουν απόλυτα μπορούμε να υψώσουμε στο τετράγωνο άρα
με πρόσθεση των (1),(2) και (3) έχουμε:
}^{2}\leq 0)
άρα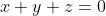




Y.Γ: Εισαι γρηγορος......(χειρίζεσαι καλα το Latex!!!
 )
)Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
dimitris001
Τιμώμενο Μέλος


ευχαριστώ
Y.Γ: Εισαι γρηγορος......(χειρίζεσαι καλα το Latex!!!)

τα μαθηματικά τα ΛΑΡΕΥΩΩΩΩΩΩΩΩΩΩΩΩΩΩ





ΥΓ. πάλι σε πρόλαβα...???

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
OChemist
Πολύ δραστήριο μέλος


ευχαριστώ
τα μαθηματικά τα ΛΑΡΕΥΩΩΩΩΩΩΩΩΩΩΩΩΩΩ
ΥΓ. πάλι σε πρόλαβα...???

 ...Ναι....Δεν πειραζει ομως....!!!Παντως και εμενα μου αρεσουν πολυ...!!!!
...Ναι....Δεν πειραζει ομως....!!!Παντως και εμενα μου αρεσουν πολυ...!!!!

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
akis95
Δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
OChemist
Πολύ δραστήριο μέλος


Λοιπον....καλουλα...τολμω να πω!!!!Οριστε πως την ελυσα εγω:Αν α,β,γ είναι διαφορετικοί απο 1 και -1 και
και
να αποδείξετε οτι

=> Για
Εστω οτι χ=0 τοτε προκυπτει οτι
y=αω και οτι ω=αy....αρα κανοντας αντικατασταση θα πρωκυψει οτι ...
=>Για
Αρα ξεκινώντας απο την [1] και αντικαθιστωντας την [2] εχουμε:
και αντικαθιστώντας στην [3] την [2]...θα παρουμε:
Οποτε πρεπει [4]=[5].....Αρα:
Ομοιως αποδεικνυεται και για την υπολοιπη σχεση συνεπως ισχυει οτι αν α,β,γ είναι διαφορετικοί απο 1 και -1 και
Αυτααααα.....απο εμενα....πιστευω σωστα την ελυσα!!!!



Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Αν ισχύει ότι
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nick18
Εκκολαπτόμενο μέλος


δημητρη μηπως αντι για διακρινουσσα μπορουμε να χρησιμοποιησουμε τους τυπους του βιετα?καλα αφου θες και τροπο λύσης...
a+b=5 άρα b=5-a
οπότε απο διακρίνουσα a=2 ή a=3
όταν όμως α=2 τότε β=5-2=3
ή
οταν α=3 τότε β=2 άρα
(α,β)=(2,3) ή (α,β)=(3,2) και τελικά
θες να το κάνω και με τον 2ο τρόπο....????
2ος ΤΡΟΠΟΣ
λοιπόν ισχύει
και άρα
άρα
όμως.....
οπότε η (1) γινεται
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Δίνεται η εξίσωσημε
με πραγματικές διαφορετικές ρίζες.
Αν ισχύει ότιδείξτε ότι μία τουλάχιστον από τις ρίζες της βρίσκεται στο διάστημα
})
Επαναφερω με ταυτοτητες
Δείξτε την συνεπαγωγη<br />
)
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
aggressive
Πολύ δραστήριο μέλος



Να βρείτε τον
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jj!
Τιμώμενο Μέλος


Από πού έμαθες προόδους εσύ;Ας βάλω μια πολύ εύκολη άσκηση πάνω στις προόδους, να τις κάνετε εσείς μια επανάληψη και να τις εμπεδώσω εγώ.
Να βρείτε τονμιας γεωμετρικής προόδου με
και
.

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Δαλιδά
Περιβόητο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jj!
Τιμώμενο Μέλος


*Τόσο καιρό νόμιζα ότι είναι αγόρι

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
sydney96
Δραστήριο μέλος


Ας βάλω μια πολύ εύκολη άσκηση πάνω στις προόδους, να τις κάνετε εσείς μια επανάληψη και να τις εμπεδώσω εγώ.
Να βρείτε τονμιας γεωμετρικής προόδου με
και
.
Το χειρότερο κεφάλαιο με διαφορά φέτος.Μεγάλη η ανακούφιση όταν το τελειώσαμε.
Εσύ βρε που τα έμαθες αυτά;Κάτσε ασχολήσου με κανένα απόλυτο καλύτερα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
aggressive
Πολύ δραστήριο μέλος


Ας βάλω μια πολύ εύκολη άσκηση πάνω στις προόδους, να τις κάνετε εσείς μια επανάληψη και να τις εμπεδώσω εγώ.
Να βρείτε τονμιας γεωμετρικής προόδου με
και
.
Η λύση στην άσκηση για όσους ενδιαφέρονται...
Διαιρούμε κατά μέλη...
1) Για
2) και για
1) Για
2) και για
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
aggressive
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 31 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

