α)
Πρέπει
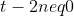
και
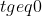
από τους περιορισμούς.Αρα τελικά πρέπει
)
.Παρατηρούμε οτι το ένα ανήκει στο διάστημα αυτό(άκρο ολοκλήρωσης) και άρα το πεδίο ορισμού της f είναι το διάστημα που ζητάμε(το [0,2) δηλαδή).
β)
=(int_{1}^{x}frac{sqrt{t}-1}{t-2}dt)'=frac{sqrt{x}-1}{x-2})
Από πίνακα μονοτονίας καταλήγουμε οτι η f είναι γνησίως αύξουσα στο [0,1] και γνησίως φθίνουσα στο [1,2) και έχει συνεπώς μέγιστο για x=1 το f(1)=0.Άρα προφανώς
leq f(1)=0prec 2prec 2+e^x )
και αρα η δοθείσα εξίσωση δεν έχει λύση
γ)
=frac{sqrt{x}-1}{x-2})
.Μόνο κατακόρυφες ασύμτωτες αναζητούμε(αφού to x ανήκει στο [0,2) ).Με απλό τρόπο δείχνουμε οτι χ=2 κατακόρυφη ασύμπτωτη.
δ)
Για χ=1 προφανής ρίζα.Θεωρώ έπειτα τη συνάρτηση g(x)=xf(x) και εφαρμόζω για αυτη θ rolle στο [0,1].Η παράγωγος της συνάρτησης που θεώρησα είναι στην ουσία η xf'(x)+f(x) η οποία έχει μια τουλάχιστον ρίζα(οπως αποδείξαμε με το θ rolle) στο (0,1).Συνεπώς συνολικά 2 ρίζες στο(0,2)--->η x=1 και μια άλλη(έστω x0) στο (0,1).
ε)
dx right|=-int_{0}^{1}f(x)dx=-int_{0}^{1}f(x)dx=-int_{0}^{1}int_{1}^{x}frac{sqrt{t}-1}{t-2}dt=-int_{0}^{1}(x)'int_{1}^{x}frac{sqrt{t}-1}{t-2}dt)
=.....πράξεις(ένα διπλό ολοκλήρωμα είναι στην ουσία)


 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki
 Το μυαλο μου πηγε σε αποσταση σημειου απο ευθεια (μη με βρισετε αν ειναι μπουρδα
Το μυαλο μου πηγε σε αποσταση σημειου απο ευθεια (μη με βρισετε αν ειναι μπουρδα  μετα τις εξετάσεις ίσως κατσω να το βγάλω γεωμετρικα :xixi:
μετα τις εξετάσεις ίσως κατσω να το βγάλω γεωμετρικα :xixi:

