kvgreco
Εκκολαπτόμενο μέλος


Αν αυτό δεν είναι η επιτομή της ειρωνείας Στέλιο τότε τι είναι?Εγώ τώρα μαθαίνω.Δεν είμαι ο... Καραθεοδωρής! Από σας τους εμπειρότερους περιμένω.Θα σκεφτώ αυτά που θα γράψει ο giannis αλλά δεν παύει να είμαστε συμμαθητές.Εσένα και το riemman80 θα φιλτράρω να πάρω όσα λέτε.1) Δεν έχω χρόνο να κάτσω να δω τη λύση. Για να το λές, έτσι θα 'ναι.
Αλλά άσε.Απόψε είναι η γιορτή της Αγάπης κι εμείς ψάχνουμε αιτίες να είμαστε σε ένταση?
Στέλιο στο μήνυμα #33 γιά βάλε όπου x την f(x) στη σχέση με την παράγωγο της αντίστροφης.Νομίζω υπάρχει λάθος στη σχέση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Undead
Εκκολαπτόμενο μέλος


με cot συμβολίζουμε την συνεφαπτομένη
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mostel
Πολύ δραστήριο μέλος


Αν αυτό δεν είναι η επιτομή της ειρωνείας Στέλιο τότε τι είναι?Εγώ τώρα μαθαίνω.Δεν είμαι ο... Καραθεοδωρής! Από σας τους εμπειρότερους περιμένω.Θα σκεφτώ αυτά που θα γράψει ο giannis αλλά δεν παύει να είμαστε συμμαθητές.Εσένα και το riemman80 θα φιλτράρω να πάρω όσα λέτε.
Αλλά άσε.Απόψε είναι η γιορτή της Αγάπης κι εμείς ψάχνουμε αιτίες να είμαστε σε ένταση?
Hey... Εσύ ψάχνεις λόγους να μαλώσεις μου φαίνετια. Σου λέω ότι δεν έχω χρόνο και για να λες ότι θα έχει λάθος στην παραγώγιση, που δεν είναι και τόσο τραγικό να την κάνεις, αφού την έχεις τσεκάρει, εμπιστεύομαι αυτό που λες, και επομένως σου λέω ότι μάλλον δίκιο θα χεις.
ΦΙλικά
Υσ: Ο Γιάννης φοιτητής στο μαθηματικό, απλώς δεν έχει αλλάξει την τάξη του από πέρσι :p
-----------------------------------------
Στέλιο στο μήνυμα #33 γιά βάλε όπου x την f(x) στη σχέση με την παράγωγο της αντίστροφης.Νομίζω υπάρχει λάθος στη σχέση.
Δεν ήταν αυτό ακριβώς, ένα f' μου έφυγε. Δες αναλυτικά εδώ:
https://en.wikipedia.org/wiki/Inverse_functions_and_differentiation
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mostel
Πολύ δραστήριο μέλος



Μετασχηματίζεται σε:
Μετά πάει αυτόματο πιλότο
Στέλιος
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mostel
Πολύ δραστήριο μέλος


Υπολογίστε το
με cot συμβολίζουμε την συνεφαπτομένη
Θα δώσω ιδέα, αλλά δεν παίζει να κάτσω να τη λύσω, έχει πολλές πράξεις

Γράφεται και:
Όμως:
Άρα:
Επίσης:
Κάνουμε κ αυτή αντικατάσταση πάνω, και έτσι έχουμε μόνο άγνωστο το

Σίγουρα υπάρχει κάτι πιο σύντομο κ κανάς μυστήριος τριγωνομετρικός τύπος που κάνει το γινόμενο αυτό άθροισμα, αλλά είναι το πρώτο πράγμα που μου 'ρθε στο μυαλό.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
fountototeratin
Νεοφερμένο μέλος


το ολοκληρωμα απο το 1 μεχρι x της f(t) + το ολοκληρωμα απο x μεχρι 1 της g(t) (ισουται)=χ^2-2x+1.
για καθε XεR και εστω Cf και Cg οι γραφικες τους συναρτησεις.εστω οτι η εξισωση f(x)=0 εχει 2 λυσεις ρ1 και ρ2 με ρ1<1<ρ2.
Α.να δειξετε οτι:
1.η εξισωση g(x)=0, εχει τουλαχιστον μια λυση στο διαστημα (ρ1,ρ2).
2.υπαρχει ενα τουλαχιστον ξε(ρ1,ρ2) τετοιο ωστε g'(ξ)= -2.
Β.αν η συναρτηση g ειναι κυρτη στο R, να αποδειξετε οτι:
1.η συναρτηση f ειναι κυρτη στο R.
2.η f εχει ενα μονο ελαχιστο στο R, το οποιο παρουσιαζεται στο σημειο x=ξ του ερωτηματος Α,2.
3.να υπολογισετε το εμβαδον του χωριου που περιεκλειεται απο τις Cf,Cg και τον αξονα των y.
(ΤΗΝ ΕΛΥΣΑ ΣΕ 6 ΛΕΠΤΑ ΚΑΙ 21 ΔΕΥΤΕΡΟΛΕΠΤΑ!)
καλη επιτυχια!!!
(οποιος θελει την λυση να μου πει!!)
ΚΑΙ ΜΙΑ ΑΛΛΗ!!!!!!!!!!!!!!
εστω οτι f:R=R ωστε το ολοκληρωμα απο X μεχρι y της f(t) ειναι μικροτερο (<) απο f(x+y) για καθε x,y εR.Ναδειξετε οτι:
1.η φ:R=R με φ(x)= e^-Χ * (επι) το ολοκληρωμα απο το 0 μεχρι x της f(t) ειναι αυξουσα στο R.
2.να αποδειξετε οτι:ισχυει 2007*το ολοκληρωμα απο 0 μεχρι το ln2006 της f(t) ειναι μικροτερο (<) απο2006*το ολοκληρωμα απο 0 μεχρι το ln2007 της f(t).
3.υπαρχει χε(1,2) ωστε: (χ-1)*f(x)= το ολοκληρωμα απο 0 μεχρι χ της f(t).
καλη επιτυχια!!!!
(την ελυσα σε 10λεπτα κ 26δευτερολεπτα!!!)
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Undead
Εκκολαπτόμενο μέλος


Έχουμε
A)
παραγωγίζοντας παίρνουμε
και ξαναπαραγωγίζοντας έχω
Οπότε εφόσον g συνεχής στο
άρα
από Θεώρημα Bolzano παίρνουμε το ζητούμενο
Εφαρμόζω το Θεώρημα Rolle στην f στο
και με
B)
Έχω
Παρατηρούμε ότι για το παραπάνω ξ
με
με
άρα
Τέλος το εμβαδόν θα είναι ίσο με το
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
kvgreco
Εκκολαπτόμενο μέλος


α) Η f είναι συνεχής άρα ορίζεται η συνάρτηση ολοκλήρωμα που είναι παραγωγίσιμη, ο δε άλλος προσθετέος όρος είναι συνάρτηση πολυωνυμική άρα παραγωγίσιμη, οπότε και η F είναι παραγωγίσιμη με F'(x)=f(x)+x/2-1
β) Έστω x1<x2 τοτε,
2(f(x1)-f(x2))<x2-x1=>f(x1)+(x1/2)<f(x2)+(x2/2)=>f(x1)+(x1/2)-1<f(x2)+(x2/2)-1=>F'(x1)<F'(x2) άρα η F' είναι γνησίως αύξουσα οπότε η F είναι κυρτή.
Χρόνια Πολλά. Άντε ξυπνήστε.Πάσχα των Ελλήνων Πάσχα σήμερα.Ας ξεδώσουμε λιγάκι.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ΗΣΙΟΔΟΣ
Νεοφερμένο μέλος
ΗΣΙΟΔΟΣ
Νεοφερμένο μέλος
galois01
Νεοφερμένο μέλος


ΚΑΙ ΜΙΑ ΑΛΛΗ!!!!!!!!!!!!!!
εστω οτι f:R=R ωστε το ολοκληρωμα απο X μεχρι y της f(t) ειναι μικροτερο (<) απο f(x+y) για καθε x,y εR.Ναδειξετε οτι:
1.η φ:R=R με φ(x)= e^-Χ * (επι) το ολοκληρωμα απο το 0 μεχρι x της f(t) ειναι αυξουσα στο R.
2.να αποδειξετε οτι:ισχυει 2007*το ολοκληρωμα απο 0 μεχρι το ln2006 της f(t) ειναι μικροτερο (<) απο2006*το ολοκληρωμα απο 0 μεχρι το ln2007 της f(t).
3.υπαρχει χε(1,2) ωστε: (χ-1)*f(x)= το ολοκληρωμα απο 0 μεχρι χ της f(t).
καλη επιτυχια!!!!
(την ελυσα σε 10λεπτα κ 26δευτερολεπτα!!!)
α)H Φ είναι παραγωγίσιμη επμένως
διότι από την υπόθεση θέτοντας y=0 παίρνουμε
Επομένως η Φ είναι γνησίως αύξουσα
β)
και επειδή η Φ είναι γνησίως αύξουσα παίρνουμε
γ) Θέτουμε
για χ>0 παίρνουμε Φ(χ)>0 επομένως
από την υπόθεση για y=0 και για χ=2 παίρνουμε
Eπομένως η F ικανοποιεί τις υποθέσεις του Θ. Bolzano οπότε προκύπτει το ζητούμενο.
Χριστός Ανέστη και Χρόνια Πολλά σε όλους

Κώστας

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Gianmaria
Νεοφερμένο μέλος


που να το βΛύστε στοτην εξίσωση
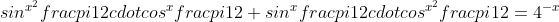
 ρουμε αυτο;πρωτακια ειμαστε..
ρουμε αυτο;πρωτακια ειμαστε..Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
djimmakos
Διάσημο μέλος


που να το βρουμε αυτο;πρωτακια ειμαστε..
Τότε τι δουλειά έχεις στην κατηγορία της Γ' λυκείου;

Υπάρχει και αντίστοιχη κατηγορία για την Α' Γυμνασίου.

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
matina91
Νεοφερμένο μέλος


α)Να αποδειξετε οτι :
i) f '(x)=1+[f(x)/x] , x>0
ii) f(x)=lnx , x>0
β) Να λυσετε την εξισωση 2f(x)={x}^{2}-1
γ) Να βρειτε το εμβαδον του χωριου που περικλείεται απο την {C}_{f} τον αξονα x'x και την ευθεια x={e}^{-1}
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Undead
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
fountototeratin
Νεοφερμένο μέλος


παω στη σχεση e^χ^2 *(χ^3+χ) =1/2 e^χ^2 *2χ(χ^2+1)
παω στο ολοκληρωμα και:1/2 ολοκληρωμα e^u *(u+1) du
τωρα κατα παραγοντες και 1/2 ολοκληρωμα (e^u)' * (u+1) du =
1/2 e^u *(u+1) - 1/2 ολοκληρωμα e^u * (u+1)' du=
1/2 e^u * (u+1) - 1/2 e^u * 1.
μετα κανε αντικατασταση u=χ^2!!
καλη επιτυχια!!
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Tas
Νεοφερμένο μέλος
cheery
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Tas
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
fountototeratin
Νεοφερμένο μέλος


και επειδη το e ειναι υψωμενο η στην x^2 δεν ξερεις την αρχικη του γιατι δεν ειναι e^2x!!!!!!!!!!!!!!!!!!!!!!
αρα παει μονο με αλλαγη μεταβλητης!!!!!
δειτε την λυση μου πανω!!!και πως του την εχω γραψει γιατι ετσι ειναι η σωστη!
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 290 μέλη διάβασαν αυτό το θέμα:
- mikke
- hihat1
- thepigod762
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- nearos
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

