Άσκηση
(Θ.Bolzano)
Αν η F συνεχείς στο [1,2] και F(1)=F(2) τότε : Να δείξεις ότι υπάρχει ένα τουλάχιστον ξe[1,2) ώστε F(ξ)=F(ξ+1/2).
Κατά τη γνώμη μου καλή άσκηση!
Θεωρώ τη συνάρτηση
=f(x) - f\left(x+\frac{1}{2} \right) \\ \ \\ g(1) = f(1)-f\left(\frac{3}{2} \right) \\ g\left(\frac{3}{2} \right) = f\left(\frac{3}{2} \right) - f(2) \\ \ \\ g(1) + g\left(\frac{3}{2} \right)=0\ (1))
έστω ότι η συνεχής g δεν έχει ρίζες στο διάστημα
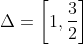
Από συνέπειες Θ. Bolzano η g θα διατηρεί σταθερό πρόσημο.
Έστω g (x) > 0, στο Δ, τότε
 + g\left(\frac{3}{2} \right)>0)
άτοπο από (1)
Όμοια για g (x) < 0 στο Δ.
-----------------------------------------
Έχω φάει κόλλημα με αυτή..
Αν f συνεχής νδο, αν ισχύει f(1/3)+f(2/3)=32/9, τότε η f(x)=2 έχει τουλάχιστον μιά πραγματική ρίζα
Αντιπαράδειγμα
f (x) = 16/9 , για κάθε x πραγματικό
f συνεχής (σταθερή)
f(1/3)+f(2/3)=32/9
η εξίσωση f(x) = 2 είναι αδύνατη.
Κάτι λέιπει από την άσκηση
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki


 Τζαμπα παιδευομουν με δαυτη τοσες ωρες...
Τζαμπα παιδευομουν με δαυτη τοσες ωρες... 
