riemann80
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
riemann80
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


Α.
Δίνονται οι μιγαδικοί αριθμοί z και w με
Aν z(w-1) + iw = 0 και |w|=2, να αποδείξετε ότι:
α) |3z+4i|=2
β) O γεωμετρικός τόπος των εικόνων του μιγαδικού
Β.
Δίνεται η συνάρτηση
Γ.
Για τους μιγαδικούς u και t των προηγούμενων ερωτημάτων να αποδείξετε ότι
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Μια άσκηση που έπεσε σαν θέμα στο διαγώνισμα του πρώην φροντιστηρίου μου:
Α.
Δίνονται οι μιγαδικοί αριθμοί z και w με
Aν z(w-1) + iw = 0 και |w|=2, να αποδείξετε ότι:
α) |3z+4i|=2
β) O γεωμετρικός τόπος των εικόνων του μιγαδικούείναι κύκλος με κέντρο Κ(1,0) και ακτίνα ρ=2
Β.
Δίνεται η συνάρτησημε
, όπου t=α+βi, α,β
με
, μιγαδικός αριθμός. Αν
, να αποδείξετε ότι ο γεωμετρικός τόπος των εικόνων του μιγαδικού t είναι κύκλος.
Γ.
Για τους μιγαδικούς u και t των προηγούμενων ερωτημάτων να αποδείξετε ότι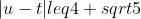
A) i) Λυνεις ως προς w και μετα με πραξεις βγαινει
ii) Αρκει |u-1|=2 αντικατασταση και βγηκε
Β) συζηγης και βγαινει
Γ)μεγιστη αποσταση 2 κυκλων αν δεν κανω λαθος
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


χμμ μπορείς να παραθέσεις τις λύσεις?A) i) Λυνεις ως προς w και μετα με πραξεις βγαινει
ii) Αρκει |u-1|=2 αντικατασταση και βγηκε
Β) συζηγης και βγαινει
Γ)μεγιστη αποσταση 2 κυκλων αν δεν κανω λαθος

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


χμμ μπορείς να παραθέσεις τις λύσεις?
Τρεχω και δεν φτανω με αυτα που εχω δεν μπορω

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


αα οκ :no1:Τρεχω και δεν φτανω με αυτα που εχω δεν μπορω
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Μια άσκηση που έπεσε σαν θέμα στο διαγώνισμα του πρώην φροντιστηρίου μου:
Α.
Δίνονται οι μιγαδικοί αριθμοί z και w με
Aν z(w-1) + iw = 0 και |w|=2, να αποδείξετε ότι:
α) |3z+4i|=2
β) O γεωμετρικός τόπος των εικόνων του μιγαδικούείναι κύκλος με κέντρο Κ(1,0) και ακτίνα ρ=2
Β.
Δίνεται η συνάρτησημε
, όπου t=α+βi, α,β
με
, μιγαδικός αριθμός. Αν
, να αποδείξετε ότι ο γεωμετρικός τόπος των εικόνων του μιγαδικού t είναι κύκλος.
Γ.
Για τους μιγαδικούς u και t των προηγούμενων ερωτημάτων να αποδείξετε ότι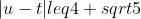
Α) α)
αλλα αυτο που εχω μεσα στο μετρο δεν μου βγαινει ισο με το ζητουμενο,οποτε εδω θα χρειαστω τη βοήθειά σου
β)
Αρα Μ(u) ανηκουν σε κυκλο με K(1,0) και ρ1=2
Β)
Αρα Μ(t) ανηκουν σε κυκλο με Λ(0,-2) και ρ2=2
Γ)
Εφόσον |ρ1-ρ2|<(ΚΛ)<ρ1+ρ2 οι κύκοι τεμνοται. Με σχημα βλεπουμε οτι
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


Α) α)
+iw=0Leftrightarrow w=frac{z}{z+i}Rightarrow |w|=|frac{z}{z+i}|Leftrightarrow |frac{z}{z+i}|=2 )
αλλα αυτο που εχω μεσα στο μετρο δεν μου βγαινει ισο με το ζητουμενο,οποτε εδω θα χρειαστω τη βοήθειά σου
β)
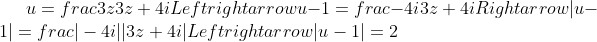
Αρα Μ(u) ανηκουν σε κυκλο με K(1,0) και ρ1=2
Β)
=0Leftrightarrow lim_{xrightarrow +propto }frac{{x}^{2}+{|t|}^{2}x+2-{x}^{2}+4Im(t)x-3}{sqrt{{x}^{2}+{|t|}^{2}x+2}+sqrt{{x}^{2}-4Im(t)x+3}}=0Leftrightarrow lim_{xrightarrow +propto }frac{x[{|t|}^{2}+4Im(t)-frac{1}{x}]}{x[sqrt{1+frac{{|t|}^{2}}{x}+frac{2}{{x}^{2}}}+sqrt{1-frac{4Im(t)}{x}+frac{3}{{x}^{2}}}]}}}=0Leftrightarrow frac{{|t|}^{2}+4Im(t)}{2}=0Leftrightarrow {alpha }^{2}+{beta }^{2}+4beta =0 )
Αρα Μ(t) ανηκουν σε κυκλο με Λ(0,-2) και ρ2=2
Γ)
Εφόσον |ρ1-ρ2|<(ΚΛ)<ρ1+ρ2 οι κύκοι τεμνοται. Με σχημα βλεπουμε οτι
+{rho }_{1}+{rho }_{2}=sqrt{5}+4 )
A)
α) δημιουργείς τις εξής σχέσεις:
και
και γνωρίζουμε από ιδιότητες μιγαδικών ότι
άρα από (1) και (2) βγαίνει το ζητούμενο
β) ωραίος
Β. σωστός
Γ. πολύ ωραίος (μην παραλείψεις να κάνεις σχήμα αν πέσει τέτοια άσκηση)
β' τρόπος:
Σύμφωνα με την τριγωνική ανισότητα έχουμε
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Δίνεται η εξίσωση:
α) Να παραστήσετε γεωμετρικά το σύνολο των μιγαδικών z που επαληθεύουν την παραπάνω εξίσωση.
β) Αν
γ) Αν
Και μια ευχή για το 2010: Εύχομαι φέτος η συναρτηση της ευτυχιας να είναι γνησίως αύξουσα και το όριο της χαράς να τείνει στο +οο

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Για δείτε αυτη:
Δίνεται η εξίσωση:
α) Να παραστήσετε γεωμετρικά το σύνολο των μιγαδικών z που επαληθεύουν την παραπάνω εξίσωση.
β) Ανείναι δύο λύσεις της παραπάνω εξίσωσης, να δείξετε ότι:
γ) Ανείναι αντίστοιχα, οι τιμές των μιγαδικών
(του ερωτήματος β), για τις οποίες η παράσταση
γίνεται μέγιστη,να δείξετε ότι:
Και μια ευχή για το 2010: Εύχομαι φέτος η συναρτηση της ευτυχιας να είναι γνησίως αύξουσα και το όριο της χαράς να τείνει στο +οο
Ωραία άσκηση. Δεν παραθέτω τη λύση για να αφήσω όσους θέλουν να ασχοληθούν. Μόνο ένα tip: χρησιμοποιήστε στο γ) ερώτημα τις παραμετρικές εξισώσεις του κύκλου και θα διευκολύνετε τη ζωή σας.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Για δείτε αυτη:
Δίνεται η εξίσωση:
α) Να παραστήσετε γεωμετρικά το σύνολο των μιγαδικών z που επαληθεύουν την παραπάνω εξίσωση.
β) Ανείναι δύο λύσεις της παραπάνω εξίσωσης, να δείξετε ότι:
γ) Ανείναι αντίστοιχα, οι τιμές των μιγαδικών
(του ερωτήματος β), για τις οποίες η παράσταση
γίνεται μέγιστη,να δείξετε ότι:
Και μια ευχή για το 2010: Εύχομαι φέτος η συναρτηση της ευτυχιας να είναι γνησίως αύξουσα και το όριο της χαράς να τείνει στο +οο
α) απο την δοσμενη σχεση με πραξεις .. κυκλος με ρ=4 και K=(-2,-4)
β)|z1-z2|<=2r .Αρα |z1-z2|<=8
γ) Αν δεν κανω καποιο λαθος πρεπει να βγαινει
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Τα α,β σωστάα) απο την δοσμενη σχεση με πραξεις .. κυκλος με ρ=4 και K=(-2,-4)
β)|z1-z2|<=2r .Αρα |z1-z2|<=8
γ) Αν δεν κανω καποιο λαθος πρεπει να βγαινει?
Για το γ δουλεύεις το πρωτο μέλος και σου βγαζει το ζητουμενο
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Δηλαδη το αποτελεσμα εχει το +1 ?Τα α,β σωστά
Για το γ δουλεύεις το πρωτο μέλος και σου βγαζει το ζητουμενο
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Δηλαδη το αποτελεσμα εχει το +1 ?
Ναι..Θα διευκολυνθείς αμα δουλεψεις ξεχωριστά το
Επίσης ενα σχήμα καλο ειναι να υπαρχει
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Ναι..Θα διευκολυνθείς αμα δουλεψεις ξεχωριστά τοκαι ξεχωριστά το
Επίσης ενα σχήμα καλο ειναι να υπαρχει
H πρωτη παρασταση βγαζει μηδεν ή κανω λαθος ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Oχι δεν κανει μηδεν..Να πω οτι ενας τροπος λύσης βασιζεται σε Β λυκειουH πρωτη παρασταση βγαζει μηδεν ή κανω λαθος ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Oχι δεν κανει μηδεν..Να πω οτι ενας τροπος λύσης βασιζεται σε Β λυκειου
Ελα , το
Το ελυσα με σχημα και λιγο Β λυκειου
Και φυσικα αφου γινεται μεγιστο το
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Σωστός. μπράβο ! :no1:Ελα , το
Το ελυσα με σχημα και λιγο Β λυκειου
Και φυσικα αφου γινεται μεγιστο τοθα εχεις
, μετα πραξεις ,ουφ
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


Αν
ii)η
iii)
iv)
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 0 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 289 μέλη διάβασαν αυτό το θέμα:
- Maynard
- foxypup
- Pars3c
- mikke
- thepigod762
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- Mariosm.
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Lathy
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Dora140303
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



