lostG
Εκκολαπτόμενο μέλος


Η άσκηση ζήταγε να αποδείξεις ότι υπάρχει μιά τριάδα αριθμών διαφορετικών μεταξύ τους πού να ανήκουν στο (α,β) ώστε να αληθεύει η σχέση.
Λοιπόν εσύ το απέδειξες αφού βρήκες ξ1 στο (-1,-2/3) και ξ2 στπ(-2/3,0) και ξ=-2/3 που σου επαληθεύουν τη σχέση.
Γιατί το βασανίζεις κι άλλο?
Δείχνεις υπερβάλλοντα σεβασμό σε ένα απλό θεώρημα.Δεν είναι ανάγκη να το κάνεις αυτό.
Το θ.bolzano είναι απλά ένα εργαλείο που μας εξασφαλίζει ρίζα σε ένα ανοικτό διάστημα.Αυτό εσένα σε βοήθησε.
Δηλαδή αμφιβάλλεις ακόμη ότι δεν έχεις βρεί την τριάδα με την προηγούμενη προσπάθειά σου?
Έπειτα κάνεις λάθος με τη δεύτερή σου προσπάθεια γιατί δεν βλέπω να λέει πουθενά η άσκηση ότι η συνάρτηση f παραγωγίζεται διπλά!
Έχεις τελειώσει με τη λύση και δεν τόχεις καταλάβει.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


Λετε ε;Ηλία δεν σε καταλαβαίνω.
Η άσκηση ζήταγε να αποδείξεις ότι υπάρχει μιά τριάδα αριθμών διαφορετικών μεταξύ τους πού να ανήκουν στο (α,β) ώστε να αληθεύει η σχέση.
Λοιπόν εσύ το απέδειξες αφού βρήκες ξ1 στο (-1,-2/3) και ξ2 στπ(-2/3,0) και ξ=-2/3 που σου επαληθεύουν τη σχέση.
Γιατί το βασανίζεις κι άλλο?
Δείχνεις υπερβάλλοντα σεβασμό σε ένα απλό θεώρημα.Δεν είναι ανάγκη να το κάνεις αυτό.
Το θ.bolzano είναι απλά ένα εργαλείο που μας εξασφαλίζει ρίζα σε ένα ανοικτό διάστημα.Αυτό εσένα σε βοήθησε.
Δηλαδή αμφιβάλλεις ακόμη ότι δεν έχεις βρεί την τριάδα με την προηγούμενη προσπάθειά σου?
Έπειτα κάνεις λάθος με τη δεύτερή σου προσπάθεια γιατί δεν βλέπω να λέει πουθενά η άσκηση ότι η συνάρτηση f παραγωγίζεται διπλά!
Έχεις τελειώσει με τη λύση και δεν τόχεις καταλάβει.
Για να το κοιταξω...αφου δω τη live συνεντευξη του Τσιπρα!
 https://www.tvxs.gr/live
https://www.tvxs.gr/liveΠαντως στη 2η προσπαθεια παραγωγιζω μια καινουργια συναρτηση την F(d) ώς προς ,δεν ειναι πουθενα η f μεσα.
-----------------------------------------
Το ξανακοιταξα και ΕΠΙΜΕΝΩ ΟΤΙ ΚΑΝΩ ΛΑΘΟΣ (οξυμωρο ε;
 )
)Αν κανω θμτ στο -1,-2/3 κλπ δε βγαινει κατι! Πειτε μου που υπαρχει η διαφωνια μας.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lostG
Εκκολαπτόμενο μέλος


Λετε ε;
Για να το κοιταξω...αφου δω τη live συνεντευξη του Τσιπρα!https://www.tvxs.gr/live
Παντως στη 2η προσπαθεια παραγωγιζω μια καινουργια συναρτηση την F(d) ώς προς ,δεν ειναι πουθενα η f μεσα.
-----------------------------------------
Το ξανακοιταξα και ΕΠΙΜΕΝΩ ΟΤΙ ΚΑΝΩ ΛΑΘΟΣ (οξυμωρο ε;)
Αν κανω θμτ στο -1,-2/3 κλπ δε βγαινει κατι! Πειτε μου που υπαρχει η διαφωνια μας.
geoste πρέπει να αναλάβεις να εξηγήσεις.
Εγώ φεύγω γιά τις πρώτες διακοπές.
Εύχομαι καλά αποτελέσματα γιά όλους και καλό Καλοκαίρι.
Αν μπορώ θα μπαίνω που και πού.
See you.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


Τελικα η λυση;;;;Έστω παραγωγίσιμη συνάρτηση f: [-1,0]->[-1,0] και f(0)=-1, f(-1)=0. Να αποδείξετε ότι υπάρχουν διαφορετικά μεταξύ τουςτέτοια ώστε
f'({xi }_{2})=2+4xi )
Και η δικη μου ειναι λαθος! Δεν ειναι;
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
manos66
Εκκολαπτόμενο μέλος


Τελικα η λυση;;;;
Και η δικη μου ειναι λαθος! Δεν ειναι;
Πρώτα δείξε ότι υπάρχει ξ στο (-1 , 0) τέτοιο ώστε f (ξ) = 2ξ + 1
Έπειτα ΘΜΤ με την f στα [-1 , ξ] και [ξ , 0]
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


Μαλιστα,αλλα πώς επρεπε να το σκεφτω αυτο;Πρώτα δείξε ότι υπάρχει ξ στο (-1 , 0) τέτοιο ώστε f (ξ) = 2ξ + 1
Έπειτα ΘΜΤ με την f στα [-1 , ξ] και [ξ , 0]
Γιατι οπως βλεπετε στη 2η προσπαθεια μου πηρα γενικα να δειξω οτι f(ξ)=αξ και δεν εβγαινε. Μετα σκεφτηκα f(ξ)=αξ+β αλλα σκεφτηκα οτι το παρατραβαω!
Μαλλον δεν βλεπετε γιατι την διεγραψα... :p
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
manos66
Εκκολαπτόμενο μέλος


Μαλιστα,αλλα πώς επρεπε να το σκεφτω αυτο;
Γιατι οπως βλεπετε στη 2η προσπαθεια μου πηρα γενικα να δειξω οτι f(ξ)=αξ και δεν εβγαινε. Μετα σκεφτηκα f(ξ)=αξ+β αλλα σκεφτηκα οτι το παρατραβαω!
Μαλλον δεν βλεπετε γιατι την διεγραψα... :p
Eίχες φτάσει στο σημείο

Λύστο σαν εξίσωση 2ου βαθμού ως προς f (m)
Η μια από τις δύο ρίζες είναι η 2m + 1
f (m) = 2m + 1
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


πωωωω!Σωστα. Τι ωραια!Eίχες φτάσει στο σημείο
Λύστο σαν εξίσωση 2ου βαθμού ως προς f (m)
Η μια από τις δύο ρίζες είναι η 2m + 1
f (m) = 2m + 1

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


Έστω η εξισωσηΆντε ρε παιδιά, βάλτε καμιά δύσκολη άσκηση.


ι)να δειξετε οτι η (1) δεν εχει πραγματικες ριζες
ιι)αν






Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


Έστω



Αν



α)


β) Για κάθε



γ) Η εξίσωση


ΥΓ Πώς γραφουμε το -απειρο στο λατεχ;
-----------------------------------------
Θεμα απο Ρουμανικο Διαγωνισμο
Κατι μου θυμιζει...εσας;
Έστω f συνεχής συνάρτηση στο [0,1] με
α) Η συνάρτηση
διάφορο του μηδενός και
Rolle στο [0 , 1]
β) Υπάρχει
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


ΘΕΜΑ ΕΜΕ 2008 -πολυ ωραιο-
Έστωσυνεχής συνάρτηση με για κάθε
για κάθε

Ανείναι μια αρχική συνάρτηση της στο
στο , να αποδείξετε ότι :
, να αποδείξετε ότι :
α)για κάθε

β) Για κάθε, υπάρχει έτσι , ώστε
έτσι , ώστε .
.
γ) Η εξίσωσηέχει άπειρες λύσεις στο .
.
ΥΓ Πώς γραφουμε το -απειρο στο λατεχ;
α) Η f είναι συνεχής στο R, οπότε έχει αρχικές συναρτήσεις στο R. Επειδή η F είναι αρχική της f στο R τότε είναι παραγωγίσιμη στο R και ισχύει F'(x)=f(x) για κάθε x ανήκει R
Θεωρώ την αντικατάσταση u=x+t => t=u-x και du=dt, u2=x+x=2x και u1=x+0=x. Συνεπώς
Άρα
β) H F είναι παραγωγίσιμη στο R, οπότε και συνεχής στο R.
Για k<0 είναι k+k<k => 2k<k
Η F είναι συνεχής στο [2k,k] και παραγωγίσιμη στο (2k,k). Σύμφωνα με το θεώρημα μέσης τιμής υπάρχει
Συνεπώς
γ)
Αν f(k)=0 τότε
Αν f(k) διάφορο του 0 τοτε
Σε κάθε περίπτωση, η εξίσωση f(x)=0 έχει άπειρες λύσεις στο
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


για το (γ) να πω και τι σκεφτηκα εγω:α) Η f είναι συνεχής στο R, οπότε έχει αρχικές συναρτήσεις στο R. Επειδή η F είναι αρχική της f στο R τότε είναι παραγωγίσιμη στο R και ισχύει F'(x)=f(x) για κάθε x ανήκει R
Θεωρώ την αντικατάσταση u=x+t => t=u-x και du=dt, u2=x+x=2x και u1=x+0=x. Συνεπώς
Άραγια κάθε x ανήκει R.
β) H F είναι παραγωγίσιμη στο R, οπότε και συνεχής στο R.
Για k<0 είναι k+k<k => 2k<k
Η F είναι συνεχής στο [2k,k] και παραγωγίσιμη στο (2k,k). Σύμφωνα με το θεώρημα μέσης τιμής υπάρχειτέτοιο ώστε:
Συνεπώςγια κάθε
γ)όπου
και
.
Αν f(k)=0 για κάθετότε
ισχύει f(x)=0 για κάθεπου σημαίνει ότι η εξίσωση f(x)=0 έχει άπειρες λύσεις στο
.
Ανγια κάθε
όπου
, τότε υπάρχουν ν μη αλληλεπικαλυπτόμενα διαστήματα
τέτοια ώστε
για κάθε
σε κάθε ένα από τα οποία υπάρχει τουλάχιστον ένα
τέτοιο ώστε
. Άρα η εξίσωση f(x)=0 έχει άπειρες λύσεις στο
.
Αν, τότε επειδή η f είναι συνεχής στο
υπάρχει σύμφωνα με το θεώρημα Bolzano τουλάχιστον ένα
τέτοιο ώστε
. Επομένως υπάρχουν ν μη αλληλεπικαλυπτόμενα διαστήματα
τέτοια ώστε
για κάθε
σε κάθε ένα από τα οποία υπάρχει τουλάχιστον ένα
τέτοιο ώστε
. Άρα η εξίσωση f(x)=0 έχει άπειρες λύσεις στο
.
Σε κάθε περίπτωση, η εξίσωση f(x)=0 έχει άπειρες λύσεις στο.
Όπως απεδειχθη

δηλαδή

Αρχικα θα δειξω οτι υπαρχει ενα ΤΟΥΛΑΧΙΣΤΟ k:f(k)=0
Έστω


Αν


ατοπο.
Ομοιως αποκλειουμε και την περιπτωση

αρα υπαρχει

Από (1)

τωρα με το


Επαγωγικα δηλαδη υπαρχουν απειρα τετοια ξ. Αρα η εξισωση εχει απειρες λυσεις.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Θεμα απο Ρουμανικο Διαγωνισμο
Κατι μου θυμιζει...εσας;
Έστω f συνεχής συνάρτηση στο [0,1] με.Να αποδείξετε ότι:
α) Η συνάρτησηπου είναι ορισμένη στο [0,1] με
για x
διάφορο του μηδενός καιπληρεί τις προϋποθέσεις του θεωρήματος
Rolle στο [0 , 1]
β) Υπάρχειτέτοιο , ώστε :

α) Η f είναι συνεχής στο [0,1], οπότε η συνάρτηση
Η f είναι συνεχής στο [0,1], οπότε η συνάρτηση g(x)=xf(x) είναι συνεχής στο [0,1] και επομένως η συνάρτηση
Η συνάρτηση
Συνεπώς η συνάρτηση H απόκτά την μορφή
Οι συναρτήσεις F και G είναι συνεχείς στο [0,1] αφού είναι παραγωγίσιμες στο [0,1]. Συνεπώς είναι παραγωγίσιμες και συνεχείς στο 0 (από δεξιά).
Έχουμε:
Άρα η H είναι συνεχής (από δεξιά) στο 0
Η H είναι συνεχής στο (0,1] και ισχύει
Η H είναι συνεχής στο [0,1], παραγωγίσιμη στο (0,1) και ισχύει H(0)=H(1). Άρα η H ικανοποιεί τις προϋποθέσεις του θεωρήματος Rolle στο διάστημα [0,1].
β) Σύμφωνα με το θεώρημα Rolle, υπάρχει τουλάχιστον ένα
Θεωρώ την συνάρτηση h με τύπο
Συνεπώς
Η h είναι συνεχής στο [0,ξ], παραγωγίσιμη στο (0,ξ) και ισχύει h(0)=h(ξ). Επομένως σύμφωνα με το θεώρημα Rolle υπάρχει τουλάχιστον ένα
αφού το σύμβολο της σταθεράς ολοκλήρωσης δεν παίζει κανένα ρόλο.
Άρα υπάρχει τουλάχιστον ένα
-----------------------------------------
Παραθέτω μία άσκηση η οποία ήταν σήμερα ένα πολύ καλό θεματάκι στο Πανεπιστήμιο Πειραιά.
Να υπολογισθεί το ολοκλήρωμα.
Θεωρώ την συνάρτηση
Θεωρώ την συνάρτηση
Η F είναι παραγωγίσιμη στο διάστημα
Είναι
Θέτω
Άρα
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Ασκηση. ανκαι ισχύει οτι
να αποδειξετε οτι
.
εννοειται οτι μιλαμε για διαφορετικους μιγαδικους.
Εφόσον οριίζεται όρισμα τότε
Τριγωνομετρική μορφή του μιγαδικού αριθμού
Άρα ο w είναι φανταστικός αριθμός. Έχουμε:
Αν
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
MYLWNAS STATHIS
Νεοφερμένο μέλος


-----------------------------------------
ας τα δει και καποιος αλλος να μου πει γνωμη θα περιμενω.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


πες και το λινκ...θεματα καλα εχει στο site του φροντιστηριου ''συγχρονο'' στη θεσσαλονικη
-----------------------------------------
ας τα δει και καποιος αλλος να μου πει γνωμη θα περιμενω.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


ΑΣΚΗΣΗ 8
Αν, να δείξετε πως η εξίσωση :
,
έχει μόνο φανταστικές ρίζες.
Έστω
Θεωρώ τους μιγαδικούς αριθμούς
Έχουμε
Θεωρώ τον μιγαδικό αριθμό
Για να είναι w=0 , πρέπει να ισχύει
Για τον πραγματικό αριθμό y ισχύει
Συνεπώς η εξίσωση έχει μόνο φανταστικές λύσεις z=yi όπου ο πραγματικός αριθμός
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


υπαρχουν λυσεις αυτης της εξισωσης;Έστωκαι
όπου
. Τότε είναι
.
Θεωρώ τους μιγαδικούς αριθμούςμε
όπου
. Συνεπώς
τέτοια ώστε
για κάθε
.
Έχουμε. Συνεπώς
και
.
Θεωρώ τον μιγαδικό αριθμό. Έχουμε
όπου
και
Για να είναι w=0 , πρέπει να ισχύει, οπότε έχουμε
αφού
για κάθε
με
. Συνεπώς
, που σημαίνει ότι ο z είναι φανταστικός αριθμός και έχει την μορφή
όπου
.
Για τον πραγματικό αριθμό y ισχύει. Από την λύση της εξίσωσης προσιορίζονται οι δυνατές τιμές του πραγματικού αριθμού y.
Συνεπώς η εξίσωση έχει μόνο φανταστικές λύσεις z=yi όπου ο πραγματικός αριθμόςπροσδιορίζεται από την λύση της εξίσωσης:
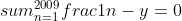
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
manos66
Εκκολαπτόμενο μέλος


ΑΣΚΗΣΗ 8
Αν, να δείξετε πως η εξίσωση :
,
έχει μόνο φανταστικές ρίζες.
ΜΙΑ ΑΚΟΜΗ ΛΥΣΗ
'Εστω ότι η εξίσωση
έχει πραγματική ρίζα, δηλαδή
Τότε
Άτοπο διότι
Άρα η εξίσωση :
αν έχει ρίζες, δεν έχει πραγματικές ρίζες.
'Εστω ότι η εξίσωση
έχει φανταστική ρίζα, δηλαδή
Τότε
H τελευταία εξίσωση έχει ακριβώς 2008 ρίζες
μια σε καθένα από τα διαστήματα (1 , 2) , (2 , 3) , ... (2008 , 2009)
(σας το αφήνω σαν άσκηση)
Άρα η αρχική εξίσωση έχει ακριβώς 2008 φανταστικές ρίζες
που είναι και μοναδικές
(το αφήνω σαν άσκηση)
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 5 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

