Mr.Blonde
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


+οο βγαίνει πάντως, όπως είναι και το λογικό αν κάνουμε σχηματάκι.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
StratosRIP
Δραστήριο μέλος


Στην ασκηση τ blonde η συναρτηση βσκ αν η f δεν ειναι παραγωγισιμη δεν θα εχει νοημα... Αnyway η απαντηση του qwerty ειναι καλιστη... Την f την εβγαλα 1/2e^x-1/2e^-x αλλα ελυσα με διαφορετικο τροπο απο αυτο π πηρατε εσεις.. Ισως να εχω λαθος.. Τλμ μετα..
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mr.Blonde
Πολύ δραστήριο μέλος


Επειδη η R ειναι κυρτη για ενα τυχαιο ξ θα ισχυει
Με γνωστη εφαρμογη(με κουραζει ο λατεχ) προκυπτει οτι
Μετα κριτηριο παρεμβολης.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
qwerty111
Πολύ δραστήριο μέλος


Αν όμως R(0)<0 δεν εφαρμόζεται το κριτήριο παρεμβολής. Εδώ έχω κολλήσει.Μπορει να μην ειναι σωστο.
Επειδη η R ειναι κυρτη για ενα τυχαιο ξ θα ισχυει
Με γνωστη εφαρμογη(με κουραζει ο λατεχ) προκυπτει οτι
Μετα κριτηριο παρεμβολης.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
drosos
Πολύ δραστήριο μέλος


Μεχρι εδω το χω φθασει θα το προσπαθησω σε λιγο! Ειμαι σε καλο δρομο;
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


και αφού είναι κυρτή προκύπτει άμεσα ότι R(x)>=R'(ξ)(χ-ξ)+R(ξ).
Oλοκληρώνοντας και τα δύο μέλη (με απόδειξη), φ(χ)>=(ολοκλήρωμα της από 0 έως χ της (R'(ξ)(τ-ξ)+R(ξ)dt))=(ολοκλήρωμα της από 0 έως χ της (R'(ξ)τ²/2-R'(ξ)ξτ+R(ξ)τ)' dt)
Με απλή εφαρμογή του γνωστού θεμελιώδους θεωρήματος Ο.Λ. προκύπτει μια συνάρτηση της μορφής R'(ξ)χ²/2-R'(ξ)ξχ+R(ξ)χ=π(χ)
η οποία στο +οο έχει όριο το +οο, αφού R'(ξ)>0
Με κριτήριο παρεμβολης στη σχέση φ(x)>=π(χ) προκύπτει το ζητούμενο όριο
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
qwerty111
Πολύ δραστήριο μέλος


Το πρόσημο του R(ξ) δεν το ξέρουμε για να βρούμε το τελευταίο όριο που γράφεις. (στην πρώτη γραμμή υποθέτω ότι εννοείς R'(ξ))Παραθέτω τη λύση, σε βασικές γραμμές, γιατί δεν ξέρω πότε θα μπορέσω να διαθέσω πάλι χρόνο:
Έστω ξ ένα σημείο της R στο οποίο δεν ισχυει R(ξ)=0(επιτρέπεται, αλλιώς δε θα ήταν γνησίως αυξουσα) , η εφαπτομένη της σε αυτό το σημείο θα είναι η y=R'(ξ)(χ-ξ)+R(ξ)
και αφού είναι κυρτή προκύπτει άμεσα ότι R(x)>=R'(ξ)(χ-ξ)+R(ξ).
Oλοκληρώνοντας και τα δύο μέλη (με απόδειξη), φ(χ)>=(ολοκλήρωμα της από 0 έως χ της (R'(ξ)(τ-ξ)+R(ξ)dt))=(ολοκλήρωμα της από 0 έως χ της (R'(ξ)τ²/2-R'(ξ)ξτ+R(ξ)τ)' dt)
Με απλή εφαρμογή του γνωστού θεμελιώδους θεωρήματος Ο.Λ. προκύπτει μια συνάρτηση της μορφής R'(ξ)χ²/2-R'(ξ)ξχ+R(ξ)χ=π(χ)
η οποία στο +οο έχει όριο το +οο, αφού R'(ξ)>0
Με κριτήριο παρεμβολης στη σχέση φ(x)>=π(χ) προκύπτει το ζητούμενο όριο
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mr.Blonde
Πολύ δραστήριο μέλος


EDIT:τωρα ειδα την λυση,αρκετα πονηρη.Σε λιγο θα βαλω και αυτης που ειχα δημοσιευσει,τα υπολοιπα ερωτηματα δηλαδη.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
qwerty111
Πολύ δραστήριο μέλος


Εγώ έχανα πρινTο όριο στο άπειρο του αχ²+βχ+γ είναι το όριο του αχ², οπότε δε μας νοιάζει το πρόσημο του R(ξ). Εκτός αν κάπου χάνω.

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


Φταίω κι εγώ που βαριέμαι το λατεξ!Εγώ έχανα πριν
Κανονικά, αν έδινε μόνο ότι είναι γνησίως αύξουσα, και πάλι γραφικά δε βγαίνει το όριο της φ +οο
 ;
;Μάλλον αγγίζουμε χωράφια έξω από τα δικά μας αν το ψάξουμε.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mr.Blonde
Πολύ δραστήριο μέλος


Παρτε μια ασκηση που μου φανηκε αρκετα δυσκολη.
Δινεται συναρτησησυνεχης για την οποια ισχυει

Να δειξετε οτι f'(0)=f(0)+1
Nα μελετηθει η f ως προς τη μονοτονια και να βρεθει το προσημο της.
Αν επιπλεον η f ειναι παραγωγισιμη στο R
Nα αποδειξετε οτι η συναρτηση g(x)=f''(x)-f(x) ειναι σταθερη
Να βρειτε τον τυπο της f.
Nα αποδειξετε οτι για οποιαδηποτε 0<α<β ,υπαρχει ξ που ανηκει στο (α,β) τετοιο ωστε

Η f' ειναι παρ/μη αφου ειναι η f αρα
Αρα g(x)=0
Eπισης
Αρα
Tελικα
Θεωρω συναρτηση g(x)=
Με θμτ στο [α,β] προκυπτει οτι υπαρχει ξ που ανηκει στο (α,β) τετοιο ωστε
Τωρα με δευτερο θμτ στην f στο [0,ξ],προκυπτει οτι υπαρχει χο που ανηκει στο (0,ξ) τετοιο ωστε
Η f' ειναι γν αυξουσα αρα εχουμε
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
qwerty111
Πολύ δραστήριο μέλος


Για το τελευταίο ερώτημα εφάρμοσα και εγώ ΘΜΤ για τη g που θεώρησες και εσύ. Αρκεί τώρα να δείξω ότι ξf'(ξ) - f(ξ)>0. Θέτω h(x)=xf'(x)-f(x). Με την μονοτονία αποδεικνύω ότι h(x)>0 για κάθε χ>0, άρα και για το ξ>α>0.Για τα 3 τελευταια,το τελευταιο βγαινει και με αλλο τροπο.Παραγωγιζοντας την αρχικη σχεση και δικαιολογωντας παραγωγισιμοτητα εχουμε
(1)
Η f' ειναι παρ/μη αφου ειναι η f αραλογω της (1)
Αρα g(x)=0
Eπισης.Απο γνωστη εφαρμογη εχουμε
.Επειδη f(0)=0 και f'(0)=1 προκυπτει c=1 αρα
Αραομως f(0)=0 αρα
Tελικα
Θεωρω συναρτηση g(x)=
Με θμτ στο [α,β] προκυπτει οτι υπαρχει ξ που ανηκει στο (α,β) τετοιο ωστε
Τωρα με δευτερο θμτ στην f στο [0,ξ],προκυπτει οτι υπαρχει χο που ανηκει στο (0,ξ) τετοιο ωστε
Η f' ειναι γν αυξουσα αρα εχουμε
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
stelios1994-4
Εκκολαπτόμενο μέλος


- Να βρείτε το
- Να αποδείξετε ότι:
για κάθε
- Να δείξετε ότι:
(1)
- Να βρείτε το γεωμετρικό τόπο των εικόνων των μιγαδικών z που ικανοποιούν την (1)
- Να αποδείξετε ότι:

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
StratosRIP
Δραστήριο μέλος


Για τα 3 τελευταια,το τελευταιο βγαινει και με αλλο τροπο.Παραγωγιζοντας την αρχικη σχεση και δικαιολογωντας παραγωγισιμοτητα εχουμε
(1)
Η f' ειναι παρ/μη αφου ειναι η f αραλογω της (1)
Αρα g(x)=0
Eπισης.Απο γνωστη εφαρμογη εχουμε
.Επειδη f(0)=0 και f'(0)=1 προκυπτει c=1 αρα
Αραομως f(0)=0 αρα
Tελικα
Θεωρω συναρτηση g(x)=
Με θμτ στο [α,β] προκυπτει οτι υπαρχει ξ που ανηκει στο (α,β) τετοιο ωστε
Τωρα με δευτερο θμτ στην f στο [0,ξ],προκυπτει οτι υπαρχει χο που ανηκει στο (0,ξ) τετοιο ωστε
Η f' ειναι γν αυξουσα αρα εχουμε
Το τελευταιο εγω τ εβγαλα με ΘΜΤ.. Τελικα καλα την βρηκα την f
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mr.Blonde
Πολύ δραστήριο μέλος


Δεν καταλαβα το Im(w)=?ΑΣΚΗΣΗ Έστω η συνεχής συνάρτησηγια την οποία
για κάθε
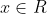
και
για την οποία
με
=1)
Αρκετά καλή.
- Να βρείτε το
- Να αποδείξετε ότι:
για κάθε
- Να δείξετε ότι:
(1)
- Να βρείτε το γεωμετρικό τόπο των εικόνων των μιγαδικών z που ικανοποιούν την (1)
- Να αποδείξετε ότι:

Kαι εγω με θμτ το εκανα.Πηρες αλλη συναρτηση;Το τελευταιο εγω τ εβγαλα με ΘΜΤ.. Τελικα καλα την βρηκα την f
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
StratosRIP
Δραστήριο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
stelios1994-4
Εκκολαπτόμενο μέλος


Το φανταστικό μέρος του w είναι ίσο με 1, είχα βάλει "/ " αντί για " \"Δεν καταλαβα το Im(w)=?
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- Maynard
- foxypup
- Pars3c
- mikke
- thepigod762
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Mariosm.
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Daemon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Lathy
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Dora140303
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



