
16-06-09

01:45
Άλλος τρόπος
Θεωρώ την συνάρτηση f(x)=6ημx-8συνx, x ανήκει R.
Η f είναι περιοδική με περίοδο T=2π αφού για κάθε x ανήκει R ισχύει:
f(x+nT)=f(x), όπου n ανήκει Z
Η f είναι συνεχής και παραγωγίσιμη στο R με παράγωγο f'(x)=6συνx+8ημx
f'(x)=0 <=> 6συνx+8ημx=0 <=> ημx=-(3/4)συνx
Αν συνx=0 τότε από την παραπάνω εξίσωση προκύπτει ημx=0 που είναι άτοπο αφού τότε (ημx)^2+(συνx)^2=0 διάφορο 1. Άρα για τις λύσεις την παραπάνω εξίσωσης ισχύει ημx διάφορο 0 και συνx διάφορο 0. Συνεπώς γράφεται ισοδύναμα
ημx=-(3/4)συνx <=> εφx=-3/4
Θέωρω) τέτοιο ώστε
τέτοιο ώστε 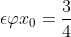 . Επειδή
. Επειδή ) τότε
τότε 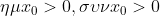
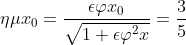
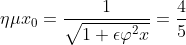
Έτσι λοιπόν έχουμε\Rightarrow x=\kappa \pi -{x}_{0},\kappa \epsilon Z)
Αν κ=2λ άρτιος τότε οι λύσεις παίρνουν την μορφή και είναι:
και είναι:
=\eta \mu \left(-{x}_{0} \right)=-\eta \mu {x}_{0}=-\frac{3}{5})
=\sigma \upsilon \nu \left(-{x}_{0} \right)=\sigma \upsilon \nu {x}_{0}=\frac{4}{5})
Αν κ=2λ+1 περιττός τότε οι λύσεις παίρνουν την μορφή και είναι:
και είναι:
=\eta \mu \left(\pi -{x}_{0} \right)=\eta \mu {x}_{0}=\frac{3}{5})
=\sigma \upsilon \nu \left(\pi -{x}_{0} \right)=-\sigma \upsilon \nu {x}_{0}=-\frac{4}{5})
=6\left(-\frac{3}{5} \right)-8\frac{4}{5}=-10)
=6\left\frac{3}{5} \right-8\left( -\frac{4}{5}\right)=10)
Η f είναι συνεχής στο , παραγωγίσιμη στο
, παραγωγίσιμη στο ) και ισχύει f'(x)<0 για κάθε
και ισχύει f'(x)<0 για κάθε ) . Συνεπώς η f είναι γνησίως φθίνουσα στο
. Συνεπώς η f είναι γνησίως φθίνουσα στο 
Η f είναι συνεχής στο , παραγωγίσιμη στο
, παραγωγίσιμη στο ) και ισχύει f'(x)>0 για κάθε
και ισχύει f'(x)>0 για κάθε ) . Συνεπώς η f είναι γνησίως αύξουσα στο
. Συνεπώς η f είναι γνησίως αύξουσα στο 
Η f είναι συνεχής στο , παραγωγίσιμη στο
, παραγωγίσιμη στο ) και ισχύει f'(x)<0 για κάθε
και ισχύει f'(x)<0 για κάθε ) . Συνεπώς η f είναι γνησίως αύξουσα στο
. Συνεπώς η f είναι γνησίως αύξουσα στο 
Συνεπώς η f παρουσιάζει τοπικό ελάχιστο στο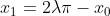 με τιμή
με τιμή =-10) και τοπικό μέγιστο στο
και τοπικό μέγιστο στο  με τιμή
με τιμή =10) τα οποία είναι και ολικά ακρότατα στο διάστημα αυτό.
τα οποία είναι και ολικά ακρότατα στο διάστημα αυτό.
Επειδή η f είναι περιοδική και σε διάστημα μιας περιόδου [2λπ, 2λπ+2π] έχει 1 ολικό ελάχιστο και ένα ολικό μέγιστο τα οποία είναι σταθερά για κάθε λ ανήκει Z, τότε τα ακρότατα αυτά είναι ολικά ακρότατα στο R και ισχύει
\leq f(x) \leq f\left( {x}_{2}\right)\Rightarrow -10\leq 6\eta \mu x-8\sigma \upsilon \nu x\leq 10\Rightarrow \left|6\eta \mu x-8\sigma \upsilon \nu x \right|\leq 10)
για κάθε x ανήκει R.
Άντε ρε παιδιά, βάλτε καμία δύσκολη άσκηση.
Θεωρώ την συνάρτηση f(x)=6ημx-8συνx, x ανήκει R.
Η f είναι περιοδική με περίοδο T=2π αφού για κάθε x ανήκει R ισχύει:
f(x+nT)=f(x), όπου n ανήκει Z
Η f είναι συνεχής και παραγωγίσιμη στο R με παράγωγο f'(x)=6συνx+8ημx
f'(x)=0 <=> 6συνx+8ημx=0 <=> ημx=-(3/4)συνx
Αν συνx=0 τότε από την παραπάνω εξίσωση προκύπτει ημx=0 που είναι άτοπο αφού τότε (ημx)^2+(συνx)^2=0 διάφορο 1. Άρα για τις λύσεις την παραπάνω εξίσωσης ισχύει ημx διάφορο 0 και συνx διάφορο 0. Συνεπώς γράφεται ισοδύναμα
ημx=-(3/4)συνx <=> εφx=-3/4
Θέωρω
Έτσι λοιπόν έχουμε
Αν κ=2λ άρτιος τότε οι λύσεις παίρνουν την μορφή
Αν κ=2λ+1 περιττός τότε οι λύσεις παίρνουν την μορφή
Η f είναι συνεχής στο
Η f είναι συνεχής στο
Η f είναι συνεχής στο
Συνεπώς η f παρουσιάζει τοπικό ελάχιστο στο
Επειδή η f είναι περιοδική και σε διάστημα μιας περιόδου [2λπ, 2λπ+2π] έχει 1 ολικό ελάχιστο και ένα ολικό μέγιστο τα οποία είναι σταθερά για κάθε λ ανήκει Z, τότε τα ακρότατα αυτά είναι ολικά ακρότατα στο R και ισχύει
για κάθε x ανήκει R.
Άντε ρε παιδιά, βάλτε καμία δύσκολη άσκηση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki






