Σπαζοκεφαλιά στα Μαθηματικά

[rolingstones]

Χαλάρωσε roling. Η άσκηση απευθύνεται σε μαθητές λυκείου. Θέλω να δω ποιος δεν θα ζητήσει διευκρίνιση για την παραγωγισιμότητα αφού στο λύκειο μαθαίνουν ότι για να είναι κυρτή, πρέπει να είναι παραγωγίσιμη. Κι εγώ στο πανεπιστήμιο τον ορισμό του λυκείου έμαθα αλλά ξέρω ότι ο ορισμός είναι άλλος και δεν είναι απαραίτητα παραγωγίσιμη η f για να είναι κυρτή (ή κοίλη).

σοβαρα δεν εμαθες τον αλλο ορισμο επειδη δε τον βρισκω στο ιντερνετ τον αλλο ορισμο τον διατυπωνεις μισο λεπτο

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Civilara]

Θα λέμε ότι η συνάρτηση f είναι κυρτή (αντίστοιχα κοίλη) στο διάστημα Δ, όταν για κάθε x,y στο διάστημα Δ και λ ανήκει [0,1] ισχύει:

f((1-λ)x+λy)<=(1-λ)f(x)+λf(y) [αντίστοιχα f((1-λ)x+λy)>=(1-λ)f(x)+λf(y)]


Σε άλλα συγγράμματα έχω δει να αναφέρεται ότι:

Θα λέμε ότι η συνάρτηση f είναι κυρτή (αντίστοιχα κοίλη) στο διάστημα Δ, όταν για κάθε x,y στο διάστημα Δ με x διάφορο y και λ ανήκει [0,1] ισχύει:

f((1-λ)x+λy)<(1-λ)f(x)+λf(y) [αντίστοιχα f((1-λ)x+λy)>(1-λ)f(x)+λf(y)]

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[rolingstones]

ενταξει ειναι σιγουρα δυσκολο να το θυμασαι αυτο οποτε υπαρχει η υπεραπλουστευση με την παραγωγισιμοτητα:iagree:

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Civilara]

Μπορεί όμως σύμφωνα με τον παραπάνω ορισμό να υπάρχει συνάρτηση f η οποία να είναι συνεχής σε διάστημα Δ, να μην είναι παραγωγίσιμη στο Δ και να είναι κυρτή (ή κοίλη). Σε αυτήν την περίπτωση τα σημεία του Δ στα οποία δεν είναι παραγωγίσιμη αποτελούν σύνολο μηδενικού μέτρου όπως συνηθίζεται να λέγεται στα μαθηματικά, δηλαδή είναι μεμονωμένα σημεία και συνεπώς πεπερασμένα σε αριθμό και δεν σχηματίζουν διάστημα.

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Undead]

3)αν επιλέξουμε 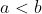ώστε τοτε απο

ΘΜΤ έχουμε


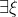ώστε


οπότε από την παραπάνω ανισότητα



παιρνωντας όρια έχουμε

άρα

σε περιοχή

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Civilara]

3)αν επιλέξουμε ώστε τοτε απο

ΘΜΤ έχουμε


ώστε


οπότε από την παραπάνω ανισότητα



παιρνωντας όρια έχουμε

άρα

σε περιοχή

Δεν είναι απόλυτα σωστό φίλε μου το σκεπτικό σου γιατί αναφέρεσαι σε συγκεκριμένη περίπτωση και όχι σε κάθε κυρτή και παραγωγίσιμη στο R συνάρτηση.

Για παράδειγμα η συνάρτηση είναι παραγωγίσιμη, γνησίως φθίνουσα και κυρτή στο R. Ως γνησίως φθίνουσα ισχύει για κάθε a,b στο R με a<b => f(b)<f(a), δηλαδή δεν υπάρχουν a,b με a<b τέτοια ώστε f(b)>f(a).

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.