Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

OChemist · 9 Αυγούστου 2012

Αρχική Δημοσίευση από P@NT?LO$:
Εστω $z=2x+yi$ , x,yεR και $\left|z \right|=2$

i)Να βρειτε το γεωμετρικο τοπο C των σημειων Μ(x,y)
ii)Αν τα Μ1 Μ2 εC,ειναι συμμετρικα ως προς τον Ο και εικονες των w1 w2 να βρειτε τη μεγιστη και ελαχιστη τιμη του μετρου $\left|{w}_{1} +{w}_{2}\right|$ καθως και τους μιγαδικους w1 w2 που παρουσιαζει το μετρο τη μεγιστη τιμη!

Ας την λυσει καποιος σας παρακαλω...

Αφου αποδειξαμε απο το (i) οτι οι εικονες του z κινουνται στην $(C):\frac{y^2}{4}+x^2=1$ ....και οι ${w}_{1},{w}_{2}$ ...ειναι συμμετρικοι ως προς το Ο(0,0) τοτε η μεγιστη αποσταση μεταξυ τους θα ειναι ιση με 2α...ενω η ελαχιστη ιση με 2β......Δηλαδη:
${\left|{w}_{1}-{w}_{2} \right|}_{min}=4$
και
${\left|{w}_{1}-{w}_{2} \right|}_{max}=2$
Υ.Γ: δεν πρεπει να ειναι w1+w2
Sorry ξεχασα να πω ποιοι μιγαδικοι ειναι.....
ειναι ο w1=2i, w2=-2i (για το μεγιστο μετρο) και ο w1=1, w2=-1(για το ελαχιστο μετρο)
Αυτααααα.....θα κανω και την απο πανω!!!!

Αρχική Δημοσίευση από P@NT?LO$:
Να βρειτε τους γεωμετρικους τοπους των εικονων των μιγαδικων z και w για τους οποιους ισχυει: $\left|z-1 \right| = \left|iz +1 \right|$ και $w=\lambda \left(1+i \right)+2i$ λeR
Μετα δειξτε οτι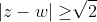 $\left|z-w \right|\geq \sqrt[]{2}$

Λοιπον εχουμε:
(i) $\left|z-1 \right|=\left|i \right|\left|z-i \right|\Leftrightarrow \left|z-1 \right|=\left|z-i \right|$ ....οποτε ο Γ.Τ των εικονων του z ανηκει στην μεσοκαθετο του τμηματος που οριζετε απο τα σημεια A(1,0) και B(0,1).....Συγκεκριμένα:
${\lambda }_{AB}=\frac{1-0}{0-1}=-1$ ...οποτε
${\lambda }_{AB}{\lambda }_{(\varepsilon )}=-1\Leftrightarrow {\lambda }_{(\epsilon )}=1$ ...(1)..επιπλεον...Εστω το Μ μεσω του τμηματος ΑΒ οποτε:
${x}_{M}=\frac{{x}_{A}+{x}_{B}}{2}=\frac{1}{2}$
${y}_{M}=\frac{{y}_{A}+{y}_{B}}{2}=\frac{1}{2}$ ...Αρα οι συντεταγμενες του σημειου ειναι $M(\frac{1}{2},\frac{1}{2})$ ...(2)...αρα απο την (1),(2)...πρικυπτει ο Γ.Τ των εικονων του z η ευθεια $(\epsilon ): y=x$
(ii)Εχουμε οτι $w=\lambda (1+i)+2i\Leftrightarrow w=\lambda +i(\lambda +2)$ ....Οποτε αν θεωρησουμε τους μιγαδικους w να οριζοντα απο την εικονα των σημειων του τυπου Γ(x,y) τοτε εχουμε οτι
$x=\lambda... [1] , y=\lambda +2\Leftrightarrow \lambda =y-2...[2]$ ...Οποτε λυνοντας και αντικαθιστωντας θα προκυψει οτι ο Γ.Τ των εικονων του w ειναι η ευθεια $(\eta ): y=x+2$
Καλα μεχρι εδω......τωρα θεωρω ενα σημειο που ανηκει στην (ε) το Κ(1,1,)...οποτε και βρισκω την ελαχιστη αποσταση του Κ απο την ευθεια (η)....οποτε:
$d(K,(\eta ))=\frac{\left|Ax+By+\Gamma \right|}{\sqrt{A^2+B^2}}=\frac{\left|1*1+1*(-1)+2 \right|}{\sqrt{1^2+(-1)^2}}=\sqrt{2}$ ....Αρα η ελαχιστη αποσταση μεταξυ των δυο ευθειων και κατ' επεκταση και των εικονων των μιγαδικων z,w ειναι ${\left|z-w \right|}_{min}=\sqrt{2}$ ....Αρα γενικα για τις εικονες των δυο μιγαδικων ισχυει οτι
$\left|z-w \right| \geq \sqrt{2}$
Αυταααααα......οτι χρειαστεις πες μου!!!!

mary-blackrose · 03-08-12

καλησπερα θα ηθελα τη βοηθεια σας στις παρακατω ασκησεις:
1)

Code:

i) Αν [LATEX]\lim _{ \chi \rightarrow 0 }{ \frac { f\left( x \right)  }{ \chi  } =\quad 3 } \quad[/LATEX]να βρεθει το [LATEX]\lim _{ \chi \rightarrow 0 }{ \frac { 2f\left( x \right) -\chi  }{ { \chi  }^{ 2 }+3\chi  }  }[/LATEX]

ii)Αν [LATEX]\lim _{ \chi \rightarrow 1 }{ \frac { f\left( x \right) -{ \chi  }^{ 3 } }{ { \chi  }^{ 2 }-1 }  } =2[/LATEX]να βρεθει το [LATEX]\lim _{ \chi \rightarrow 1 }{ \frac { f\left( x \right) -{ \chi  } }{ \sqrt { \chi  } -1 }  } [/LATEX]

2)
να βρεθει το [LATEX]\lim _{ \chi \rightarrow \sigma  }{ f\left( x \right) } [/LATEX]
i)
[LATEX]\frac { 2{ \chi  }^{ 2 }-1 }{ { \chi  }^{ 2 }+1 } \le f\left( x \right) \le \frac { 2\chi -1 }{ \chi +1 } \quad ,\chi <-1\quad \kappa \alpha \iota \quad \sigma =-\infty [/LATEX]

ii) [LATEX]\sqrt { 4{ \chi  }^{ 2 }+1 } -\chi \le f\left( x \right) +x\le \sqrt { { \chi  }^{ 2 }+1 } ,\chi >0\quad \kappa \alpha \iota \quad \sigma =+\infty [/LATEX]

Βλα · 03-08-12

Τα δύο πρώτα τα έχω βγάλει, χρειάζομαι λίγη βοήθεια στο τρίτο...

Υ.Γ: Στην πρώτη σειρά γράφει "διαφορετικοί ανά δύο"
Και στην δεύτερη "αν ισχύουν"

antwwwnis · 03-08-12

Αρχική Δημοσίευση από Βλα:
Τα δύο πρώτα τα έχω βγάλει, χρειάζομαι λίγη βοήθεια στο τρίτο...

Υ.Γ: Στην πρώτη σειρά γράφει "διαφορετικοί ανά δύο"
Και στην δεύτερη "αν ισχύουν"

Πρέπει να δείξεις ότι |z1-z2|=|z2-z3|=|z1-z3|

g1wrg0s · 03-08-12

η σχεση που σου εγραψε ο αντωνης αρκει να δειχθει διοτι αν παρατηρησεις καθε μελος ειναι το μηκος μιας πλευρας του τριγωνου .

Βλα · 03-08-12

Αρχική Δημοσίευση από antwwwnis:
Πρέπει να δείξεις ότι |z1-z2|=|z2-z3|=|z1-z3|

Το έχω καταλάβει αυτό αλλά δεν βγαίνει τίποτα...
Υψώνω στο τετράγωνο στην σχέση αυτή, αλλά δεν βγαίνει τίποτα...
ΒΓαίνει μόνο μια σχέση η οποία αν βάλω μέτρο ισχύει αλλά από τη στιγμή που βάζω μέτρο από "<=>" γίνεται "=>" οπότε δεν βγάζω τίποτα.

OChemist · 03-08-12

Αρχική Δημοσίευση από mary-blackrose:

καλησπερα θα ηθελα τη βοηθεια σας στις παρακατω ασκησεις:
1)

Code:

i) Αν [LATEX]\lim _{ \chi \rightarrow 0 }{ \frac { f\left( x \right)  }{ \chi  } =\quad 3 } \quad[/LATEX]να βρεθει το [LATEX]\lim _{ \chi \rightarrow 0 }{ \frac { 2f\left( x \right) -\chi  }{ { \chi  }^{ 2 }+3\chi  }  }[/LATEX]

ii)Αν [LATEX]\lim _{ \chi \rightarrow 1 }{ \frac { f\left( x \right) -{ \chi  }^{ 3 } }{ { \chi  }^{ 2 }-1 }  } =2[/LATEX]να βρεθει το [LATEX]\lim _{ \chi \rightarrow 1 }{ \frac { f\left( x \right) -{ \chi  } }{ \sqrt { \chi  } -1 }  } [/LATEX]

2)
να βρεθει το [LATEX]\lim _{ \chi \rightarrow \sigma  }{ f\left( x \right) } [/LATEX]
i)
[LATEX]\frac { 2{ \chi  }^{ 2 }-1 }{ { \chi  }^{ 2 }+1 } \le f\left( x \right) \le \frac { 2\chi -1 }{ \chi +1 } \quad ,\chi <-1\quad \kappa \alpha \iota \quad \sigma =-\infty [/LATEX]

ii) [LATEX]\sqrt { 4{ \chi  }^{ 2 }+1 } -\chi \le f\left( x \right) +x\le \sqrt { { \chi  }^{ 2 }+1 } ,\chi >0\quad \kappa \alpha \iota \quad \sigma =+\infty [/LATEX]

Λοιπον εχουμε:
1] (i) θετω $g(x)=\frac{f(x)}{x}\Leftrightarrow f(x)=xg(x)$ ....οποτε και $\lim_{x\rightarrow 0}g(x)=\frac{f(x)}{x}=3\Leftrightarrow \lim_{x\rightarrow 0}g(x)=3.......[1]$ ....Τωρα πας στο δοθεν οριο και αντικαθιστας την f(x) συναστησει της g(x)...Δηλαδη: $\lim_{x\rightarrow 0}\frac{2f(x)-x}{x^2+3x}\Leftrightarrow \lim_{x\rightarrow 0}\frac{2xg(x)-x}{x^2+3x}$ ...απλοποιεις το x και θα προκυψει το οριο χρησημοποιώντας την [1]...Δηλαδή: $\lim_{x\rightarrow 0}\frac{2xg(x)-x}{x^2+3x}=\lim_{x\rightarrow 0}\frac{2g(x)-1}{x+3}=\frac{5}{3}$
(ii) θετω και για το δευτερο θετω $h(x)= \frac { f\left( x \right) -{ \chi }^{ 3 } }{ { \chi }^{ 2 }-1 } \Leftrightarrow f(x)=(x^2-1)h(x)+x^3$ ....και για το οποιο παλι ισυει οτι : $\lim_{x\rightarrow 1}h(x)= \lim_{x\rightarrow 0}\frac{f(x)-x^3}{x^2-1}=2\Leftrightarrow \lim_{x\rightarrow 1} h(x)=2........[2]$ ....και τωρα θα αντικαταστησω την f(x) συναρτησει της h(x) στο δοθεν οριο...Δηλαδη: $\lim_{x\rightarrow 1}\frac{f(x)-x}{\sqrt{x}-1}=\lim_{x\rightarrow 1}\frac{(x^2-1)h(x)+x^3-x}{\sqrt{x}-1}=\lim_{x\rightarrow 1}\frac{x^2h(x)-h(x)+x^3-x}{\sqrt{x}-1}=\lim_{x\rightarrow 1}\frac{x^2(h(x)+x)-(h(x)+x)}{\sqrt{x}-1}=\lim_{x\rightarrow 1}\frac{(x^2-1)(h(x)+x)}{\sqrt{x}-1}=\lim_{x\rightarrow 1}\frac{(x-1)(x+1)(h(x)+x)(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}=\lim_{x\rightarrow 1}(x+1)(h(x)+x)(\sqrt{x}+1)=12$ ....[Σημειωση!!! Εκανα επιμεριστικη στην αρχη....μετα εβγαλα κοινους ανα δυο και τελος πολλαπλασιασα παρονομαστη και αριθμητη με τον συζηγη του παρονομαστη και εκανα απλοποιησεις]
2] Για το [2] θα βασιστω ΚΑΙ στα δυο ερωτηματα στο κριτηριο παρεμβολης: Λοιπον εχουμε οτι :
(i) $\frac { 2{ \chi }^{ 2 }-1 }{ { \chi }^{ 2 }+1 } \le f\left( x \right) \le \frac { 2\chi -1 }{ \chi +1 }$ ...οποτε
$\lim_{x\rightarrow -oo }\frac{2x^2-1}{x^2+1}=\lim_{x\rightarrow -oo }\frac{2x^2}{x^2}=\lim_{x\rightarrow -oo }2=2$ ....και
$\lim_{x\rightarrow -oo}\frac{2x-1}{x+1}=\lim_{x\rightarrow -oo}\frac{2x}{x}=\lim_{x\rightarrow -oo}2=2$ ...Αρα απο κριτηριο παρεμβολης $\lim_{x\rightarrow -oo}f(x)=2$ ....[Σημειωση!!! Βασιστηκα στο γεγονος οτι στα ορια στο απειρο παιρνεις τους μεγιστοβαθμιους στα πολυωνυμα]
(ii)Εχουμε οτι: $\sqrt { 4{ \chi }^{ 2 }+1 } -\chi \le f\left( x \right) +x\le \sqrt { { \chi }^{ 2 }+1 } ,\chi >0$
$\sqrt { 4{ \chi }^{ 2 }+1 } -2\chi \le f\left( x \right) \le \sqrt { { \chi }^{ 2 }+1 }-x$ ....Οποτε και εχουμε:
$\lim_{x\rightarrow +oo}[\sqrt{4x^2+1}-2x]=\lim_{x\rightarrow +oo}\frac{[\sqrt{4x^2+1}-2x][\sqrt{4x^2+1}+2x]]}{[\sqrt{4x^2+1}+2x]}=\lim_{x\rightarrow +oo}\frac{1}{\sqrt{4x^2+1}+2x}=0$ ...[Σημειωση!!! Πολλαπλασιασα και τον παρονομαστη που υποτιθεται οτι ειναι 1 και τον αριθμητη με την συζηγη παρασταση του αριθμιτη και στην συνεχεια εκανα πραξεις και προεκυψε το οριο]
επιπλεον....
$.....\lim_{x\rightarrow +oo}[\sqrt{x^2+1}-x]=\lim_{x\rightarrow +oo}\frac{[\sqrt{x^2+1}-x][\sqrt{x^2+1}+x]}{[\sqrt{x^2+1}+x]}=\lim_{x\rightarrow +oo}\frac{1}{\sqrt{x^2+1}+x}=0$ ...[Σημειωση!!! Μια απο τα ιδια!!!]...Συνεπως απο κριτηριο παρεμβολης $\lim_{x\rightarrow +oo}f(x)=0$
Αυτααααα...(τα λιγα!!!

)...Για Ο,ΤΙ χρειαστείς πες μου!!!!

BILL KEXA · 03-08-12

μπορεί κανείς να μου βρεί την μονοτονία της f(x)=ln( e^x -1 / e^x + 1 ) γτ σε ένα σημείο κόλλησα...ευχαριστώ

OChemist · 03-08-12

Αρχική Δημοσίευση από BILL KEXA:
μπορεί κανείς να μου βρεί την μονοτονία της f(x)=ln( e^x -1 / e^x + 1 ) γτ σε ένα σημείο κόλλησα...ευχαριστώ

Εγω στην περιπτωση αυτη θα επαιρνα τον ορισμο της μονοτονιας και θα το εβγαζα....με παραγωγηση ΠΟΛΥΥΥΥΥΥ δυσκολα (για εμενα τουλαχιστον!!!)...Ασε που βγαινει σε 4 γραμμες...Συγκεκριμένα:
Εχουμε οτι $f(x)=ln(\frac{e^x-1}{e^x+1}), \mu \varepsilon.... {A}_{f}=(0,+\infty)$
για ${x}_{1},{x}_{2}\epsilon (0,+\infty)......\mu \varepsilon .....{x}_{1}<{x}_{2}$ ....τοτε
${e}^{{x}_{1}}<{e}^{{x}_{2}}\Leftrightarrow {e}^{{x}_{1}}-1<{e}^{{x}_{2}}-1.......[1]$
${e}^{{x}_{1}}<{e}^{{x}_{2}}\Leftrightarrow {e}^{{x}_{1}}+1<{e}^{{x}_{2}}+1.....[2]$ ....Διαιρεις την [1]/[2]....(αφου ΟΛΑ ειναι θετικα)....και παιρνουμε:
$\frac{{e}^{{x}_{1}}-1}{{e}^{{x}_{1}}+1}<\frac{{e}^{{x}_{2}}-1}{{e}^{{x}_{2}}+1}$ .....και επειδη η lnx ειναι γνησιως αυξουσα σε ολο το (0,+οο) τοτε:
$ln(\frac{{e}^{{x}_{1}}-1}{{e}^{{x}_{1}}+1})<ln(\frac{{e}^{{x}_{2}}-1}{{e}^{{x}_{2}}+1})\Leftrightarrow f({x}_{1})<f({x}_{2})$ ....Αρα και η f(x) ειναι γνησιως αυξουσα στο (0,+οο) αφου για ${x}_{1}<{x}_{2}$ ...εχουμε $f({x}_{1})<f({x}_{2})$
Αυτααααα......αν κατι δεν καταλαβαινεις πες το μου!!!!

dimitris001 · 04-08-12

Αρχική Δημοσίευση από vassilakos:
Εγω στην περιπτωση αυτη θα επαιρνα τον ορισμο της μονοτονιας και θα το εβγαζα....με παραγωγηση ΠΟΛΥΥΥΥΥΥ δυσκολα (για εμενα τουλαχιστον!!!)...Ασε που βγαινει σε 4 γραμμες...Συγκεκριμένα:
Εχουμε οτι $f(x)=ln(\frac{e^x-1}{e^x+1}), \mu \varepsilon.... {A}_{f}=(0,+\infty)$
για ${x}_{1},{x}_{2}\epsilon (0,+\infty)......\mu \varepsilon .....{x}_{1}<{x}_{2}$ ....τοτε
${e}^{{x}_{1}}<{e}^{{x}_{2}}\Leftrightarrow {e}^{{x}_{1}}-1<{e}^{{x}_{2}}-1.......[1]$
${e}^{{x}_{1}}<{e}^{{x}_{2}}\Leftrightarrow {e}^{{x}_{1}}+1<{e}^{{x}_{2}}+1.....[2]$ ....Διαιρεις την [1]/[2]....(αφου ΟΛΑ ειναι θετικα)....και παιρνουμε:
$\frac{{e}^{{x}_{1}}-1}{{e}^{{x}_{1}}+1}<\frac{{e}^{{x}_{2}}-1}{{e}^{{x}_{2}}+1}$ .....και επειδη η lnx ειναι γνησιως αυξουσα σε ολο το (0,+οο) τοτε:
$ln(\frac{{e}^{{x}_{1}}-1}{{e}^{{x}_{1}}+1})<ln(\frac{{e}^{{x}_{2}}-1}{{e}^{{x}_{2}}+1})\Leftrightarrow f({x}_{1})<f({x}_{2})$ ....Αρα και η f(x) ειναι γνησιως αυξουσα στο (0,+οο) αφου για ${x}_{1}<{x}_{2}$ ...εχουμε $f({x}_{1})<f({x}_{2})$
Αυτααααα......αν κατι δεν καταλαβαινεις πες το μου!!!!

ε....αφού το έκανε ο vassilakos με τον ορισμό ας το κανω εγώ με παραγώγους....
Αρχικά βρίσκουμε το Π.Ο...πρέπει $\frac{e^x-1}{e^x+1}>0$ και επειδή $e^x>0$ εχουμε οτι $e^x+1>0(1)$ άρα πρέπει $e^x-1>0$ ....οπότε χ>0...άρα Π.Ο=(0,+οο)
Για να διευκολυνθούμε στις πράξεις κάνουμε το εξής...
$f(x)=ln(\frac{e^x-1}{e^x+1})=ln({e}^{x}-1)-ln({e}^{x}+1)$ άρα
$f'(x)=\frac{{e}^{x}}{{e}^{x}-1}-\frac{{e}^{x}}{{e}^{x}+1}=\frac{{e}^{x}({e}^{x}+1)-{e}^{x}({e}^{x}-1)}{({e}^{x}-1)({e}^{x}+1)}=\frac{{e}^{x}({e}^{x}+1-{e}^{x}+1)}{({e}^{x}-1)({e}^{x}+1)}=\frac{2{e}^{x}}{({e}^{x}-1)({e}^{x}+1)}$
Όμως, επειδή x>0....έχουμε οτι $({e}^{x}-1)({e}^{x}+1)>0$ και $2e^x>0$
άρα f '(x)>0 άρα επειδή ειναι συνεχή ως πράξεις συνεχών συναρτήσεων στο (0,+οο) η f(x) είναι γν. αύξουσα σε όλο το Π.Ο

vimaproto · 04-08-12

....Διαιρεις την [1]/[2]....(αφου ΟΛΑ ειναι θετικα)....και παιρνουμε:
Είναι έτσι?
Για κοίταξε αυτό
5<12
2<10
Διαιρώ κατά μέλη όπως λες και 2,5<1,2 είναι σωστό?
Ξανακοίταξε τη λύση σου.

vimaproto · 04-08-12

Αρχική Δημοσίευση από BILL KEXA:
μπορεί κανείς να μου βρεί την μονοτονία της f(x)=ln( e^x -1 / e^x + 1 ) γτ σε ένα σημείο κόλλησα...ευχαριστώ

Γνώμη μου είναι να ονομάσεις το κλάσμα φ(χ) και να βρεις τη μονοτονία του ως φ(χ1)-φ(χ2)=........=2(e^x1 -e^x2)/(e^x1+1)(e^x2+1)<0 αφού ο αριθμητής είναι αρνητικός και έτσι βγαίνει συνάρτηση αύξουσα και στη συνέχεια την f(x)=lnφ(x) την οποία θα βγάλεις αύξουσα στο διάστημα (0,οο)

mary-blackrose · 04-08-12

Αρχική Δημοσίευση από vassilakos:
Λοιπον εχουμε:
1] (i) θετω $g(x)=\frac{f(x)}{x}\Leftrightarrow f(x)=xg(x)$ ....οποτε και $\lim_{x\rightarrow 0}g(x)=\frac{f(x)}{x}=3\Leftrightarrow \lim_{x\rightarrow 0}g(x)=3.......[1]$ ....Τωρα πας στο δοθεν οριο και αντικαθιστας την f(x) συναστησει της g(x)...Δηλαδη: $\lim_{x\rightarrow 0}\frac{2f(x)-x}{x^2+3x}\Leftrightarrow \lim_{x\rightarrow 0}\frac{2xg(x)-x}{x^2+3x}$ ...απλοποιεις το x και θα προκυψει το οριο χρησημοποιώντας την [1]...Δηλαδή: $\lim_{x\rightarrow 0}\frac{2xg(x)-x}{x^2+3x}=\lim_{x\rightarrow 0}\frac{2g(x)-1}{x+3}=\frac{5}{3}$
(ii) θετω και για το δευτερο θετω $h(x)= \frac { f\left( x \right) -{ \chi }^{ 3 } }{ { \chi }^{ 2 }-1 } \Leftrightarrow f(x)=(x^2-1)h(x)+x^3$ ....και για το οποιο παλι ισυει οτι : $\lim_{x\rightarrow 1}h(x)= \lim_{x\rightarrow 0}\frac{f(x)-x^3}{x^2-1}=2\Leftrightarrow \lim_{x\rightarrow 1} h(x)=2........[2]$ ....και τωρα θα αντικαταστησω την f(x) συναρτησει της h(x) στο δοθεν οριο...Δηλαδη: $\lim_{x\rightarrow 1}\frac{f(x)-x}{\sqrt{x}-1}=\lim_{x\rightarrow 1}\frac{(x^2-1)h(x)+x^3-x}{\sqrt{x}-1}=\lim_{x\rightarrow 1}\frac{x^2h(x)-h(x)+x^3-x}{\sqrt{x}-1}=\lim_{x\rightarrow 1}\frac{x^2(h(x)+x)-(h(x)+x)}{\sqrt{x}-1}=\lim_{x\rightarrow 1}\frac{(x^2-1)(h(x)+x)}{\sqrt{x}-1}=\lim_{x\rightarrow 1}\frac{(x-1)(x+1)(h(x)+x)(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}=\lim_{x\rightarrow 1}(x+1)(h(x)+x)(\sqrt{x}+1)=12$ ....[Σημειωση!!! Εκανα επιμεριστικη στην αρχη....μετα εβγαλα κοινους ανα δυο και τελος πολλαπλασιασα παρονομαστη και αριθμητη με τον συζηγη του παρονομαστη και εκανα απλοποιησεις]
2] Για το [2] θα βασιστω ΚΑΙ στα δυο ερωτηματα στο κριτηριο παρεμβολης: Λοιπον εχουμε οτι :
(i) $\frac { 2{ \chi }^{ 2 }-1 }{ { \chi }^{ 2 }+1 } \le f\left( x \right) \le \frac { 2\chi -1 }{ \chi +1 }$ ...οποτε
$\lim_{x\rightarrow -oo }\frac{2x^2-1}{x^2+1}=\lim_{x\rightarrow -oo }\frac{2x^2}{x^2}=\lim_{x\rightarrow -oo }2=2$ ....και
$\lim_{x\rightarrow -oo}\frac{2x-1}{x+1}=\lim_{x\rightarrow -oo}\frac{2x}{x}=\lim_{x\rightarrow -oo}2=2$ ...Αρα απο κριτηριο παρεμβολης $\lim_{x\rightarrow -oo}f(x)=2$ ....[Σημειωση!!! Βασιστηκα στο γεγονος οτι στα ορια στο απειρο παιρνεις τους μεγιστοβαθμιους στα πολυωνυμα]
(ii)Εχουμε οτι: $\sqrt { 4{ \chi }^{ 2 }+1 } -\chi \le f\left( x \right) +x\le \sqrt { { \chi }^{ 2 }+1 } ,\chi >0$
$\sqrt { 4{ \chi }^{ 2 }+1 } -2\chi \le f\left( x \right) \le \sqrt { { \chi }^{ 2 }+1 }-x$ ....Οποτε και εχουμε:
$\lim_{x\rightarrow +oo}[\sqrt{4x^2+1}-2x]=\lim_{x\rightarrow +oo}\frac{[\sqrt{4x^2+1}-2x][\sqrt{4x^2+1}+2x]]}{[\sqrt{4x^2+1}+2x]}=\lim_{x\rightarrow +oo}\frac{1}{\sqrt{4x^2+1}+2x}=0$ ...[Σημειωση!!! Πολλαπλασιασα και τον παρονομαστη που υποτιθεται οτι ειναι 1 και τον αριθμητη με την συζηγη παρασταση του αριθμιτη και στην συνεχεια εκανα πραξεις και προεκυψε το οριο]
επιπλεον....
$.....\lim_{x\rightarrow +oo}[\sqrt{x^2+1}-x]=\lim_{x\rightarrow +oo}\frac{[\sqrt{x^2+1}-x][\sqrt{x^2+1}+x]}{[\sqrt{x^2+1}+x]}=\lim_{x\rightarrow +oo}\frac{1}{\sqrt{x^2+1}+x}=0$ ...[Σημειωση!!! Μια απο τα ιδια!!!]...Συνεπως απο κριτηριο παρεμβολης $\lim_{x\rightarrow +oo}f(x)=0$
Αυτααααα...(τα λιγα!!!)...Για Ο,ΤΙ χρειαστείς πες μου!!!!

Σ ευχαριστω πολυ !!!!Ειναι μια χαρα κατανοητα..!!!

BILL KEXA · 04-08-12

μα όμως σε ανισότητες δεν επιτρέπεται να αφαιρούμε και να διαιρούμε κατά μέλη.... τότε ??? :worry:

BILL KEXA · 04-08-12

εγω το έλυσα κάπως έτσι και δεν μπορώ να καταλάβω που έχασα την μπάλα.....

Lil_Chris · 04-08-12

Παιδιά λίγη βοήθεια!
Αν $w = \frac{z-1}{z+1}$ και η εικόνα του w κινείται στην ευθεία y=x, να δειχτεί ότι η εικόνα του z κινείται σε κύκλο.

Βλα · 04-08-12

Αρχική Δημοσίευση από Βλα:
Τα δύο πρώτα τα έχω βγάλει, χρειάζομαι λίγη βοήθεια στο τρίτο...

Υ.Γ: Στην πρώτη σειρά γράφει "διαφορετικοί ανά δύο"
Και στην δεύτερη "αν ισχύουν"

Κανείς ρε παίδες;;; :confused:

OChemist · 04-08-12

Αρχική Δημοσίευση από vimaproto:
....Διαιρεις την [1]/[2]....(αφου ΟΛΑ ειναι θετικα)....και παιρνουμε:
Είναι έτσι?
Για κοίταξε αυτό
5<12
2<10
Διαιρώ κατά μέλη όπως λες και 2,5<1,2 είναι σωστό?
Ξανακοίταξε τη λύση σου.

Αρχική Δημοσίευση από BILL KEXA:
μα όμως σε ανισότητες δεν επιτρέπεται να αφαιρούμε και να διαιρούμε κατά μέλη.... τότε ???

Αρχική Δημοσίευση από BILL KEXA:
εγω το έλυσα κάπως έτσι και δεν μπορώ να καταλάβω που έχασα την μπάλα.....

Πραγματικα....οντως....μεγαααααλη μ*****α εκανα.....Σορρυ.....Αλλα ο τροπος του BILL KEXA....ειναι πολυ εξυπνος και διορθωνει την βλακεια που εκανα..... :redface:

....Εν παση περιπτωση αν το κανεις ακριβως οπως ο BILL KEXA τοτε βγαινει με τον ορισμο...

Υ.Γ: BILL KEXA οταν τα πολλα πολλαπλασιασες δεν επρεπε να αλλαξεις (νομιζω ) την φορα της ανισωσης... :redface:

OChemist · 04-08-12

Αρχική Δημοσίευση από Βλα:
Κανείς ρε παίδες;;;

Πραγματικα το σκεφτομαι......καταληγω ΜΟΝΟ οτι $\left|{z}_{1} +{z}_{2}\right|=\left|{z}_{2}+ {z}_{3}\right|=\left|{z}_{1}+ {z}_{3}\right|$ ................που δεν ειναι ακριβως αυτο που πρεπει να αποδειχτει....!!!!

akis95 · 04-08-12

ας δωσω μια λυση

z1²+z2²+z3³=0 <=>z1z2+z3z1+z2z3=0<=>z1(z2+z3)+z2z3=0<=> -z1²=-z2z3<=>z1³=z1z2z3

κυκλικα εχουμε οτι z2³=z1z2z3 και z3³=z1z2z3 αρα z1³=z2³=z3³ αρα επεται το ζητουμενο
και το τελευταιο
αρκει νδο \Ζ1-Ζ2\=\Ζ1-Ζ3\ ΑΛΛΑΞΕ ΤΟ z1=-z2-z3 πραξεςι και τελος

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Πολύ δραστήριο μέλος

Συνημμένα

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Διάσημο μέλος

Επιφανές μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένο μέλος

Πολύ δραστήριο μέλος

Τιμώμενο Μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένο μέλος

Νεοφερμένο μέλος

Συνημμένα

Νεοφερμένο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Δραστήριο μέλος