Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

mary-blackrose · 25 Ιουλίου 2012

καλησπερα θα ηθελα τη βοηθεια σας στην παρακατω ασκηση:
Εστω συναρτηση

Code:

[LATEX]\digamma :\Re \rightarrow \Re [/LATEX] τετοια, ωστε:[LATEX] \digamma \left( \chi  \right) +1\ge \sqrt { { \chi  }^{ 2 }+1 }[/LATEX], για καθε [LATEX]\chi \quad \in \Re [/LATEX] και   [LATEX]\lim _{ \chi \rightarrow 0 }{ \frac { \digamma \left( \chi  \right)  }{ \chi  } =\ell \quad ,\ell \quad \in \Re  }[/LATEX] 
1) να βρεθει το [LATEX]\ell [/LATEX] 
Αν:
[LATEX]\digamma \left( \chi  \right) \le { \digamma  }^{ 2 }\left( \chi  \right) +\frac { { \chi  }^{ 2 } }{ \chi  } \quad[/LATEX] για καθε [LATEX]\chi \quad \in \Re [/LATEX]να αποδειξετε οτι [LATEX]\lim _{ \chi \rightarrow 0 }{  } \frac { \digamma \left( \chi  \right)  }{ { \chi  }^{ 2 } } =\frac { 1 }{ 2 } [/LATEX]

αν μπορει καποιος ας μου εξηγησει πως απο τη σχεση που μου δινει θα καταφερω να φτιαξω τη σχεση που χρειαζομαι .........

OChemist · 26 Ιουλίου 2012

Αρχική Δημοσίευση από P@NT?LO$:
Εστω z,wεC με $\left|z \right|=1$ και $\left|w \right|=\sqrt{2}$
i. Να δειξετε οτι z+w-zw+1=0 $\Leftrightarrow$ 2z+w+zw-2=0
ii.Aν z+w-zw+1=0 , να βρειτε τους z και w
iii.Να δειξετε οτι: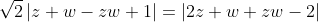 $\sqrt{2}\left|z+w-zw+1 \right|=\left|2z+w+zw-2 \right|$

To (iii):
Γενικα ισχυει οτι: $\left|z+w+1-zw \right|=\left|\bar{z}+\bar{w}+1-\bar{z}\bar{w} \right|$ το μετρο ενος μιγαδικου ειναι ισο με το μετρο του συζηγη του.Οποτε αφου... $\left|z \right|=1\Leftrightarrow \bar{z}=\frac{1}{z}$ ......και..... $\left|w \right|=2\Leftrightarrow \bar{w}=\frac{2}{w}$ ...τοτε....
$\left|z+w+1-zw \right|=\left|\bar{z}+\bar{w}+1-\bar{z}\bar{w} \right|\Leftrightarrow$
$\left|z+w+1-zw \right|=\left|\frac{1}{z}+\frac{2}{w}+1-\frac{2}{zw} \right|\Leftrightarrow$
$\left|z+w+1-zw \right|=\frac{\left|w+2z+zw-2 \right|}{\left|zw \right|}\Leftrightarrow$
$\left|z+w+1-zw \right|=\frac{\left|w+2z+zw-2 \right|}{\sqrt{2}}\Leftrightarrow$
$\sqrt{2}\left|z+w+1-zw \right|=\left|w+2z+zw-2 \right|$
Ετοιμος.....!!!!!Οριστε....για οποιαδηποτε απορία ρωτα με....!!!

Αρχική Δημοσίευση από mary-blackrose:
καλησπερα θα ηθελα τη βοηθεια σας στην παρακατω ασκηση:
Εστω συναρτηση

Code:

[LATEX]\digamma :\Re \rightarrow \Re [/LATEX] τετοια, ωστε:[LATEX] \digamma \left( \chi \right) +1\ge \sqrt { { \chi }^{ 2 }-1 }[/LATEX], για καθε [LATEX]\chi \quad \in \Re [/LATEX] και [LATEX]\lim _{ \chi \rightarrow 0 }{ \frac { \digamma \left( \chi \right) }{ \chi } =\ell \quad ,\ell \quad \in \Re }[/LATEX] 1) να βρεθει το [LATEX]\ell [/LATEX] Αν: [LATEX]\digamma \left( \chi \right) \le { \digamma }^{ 2 }\left( \chi \right) +\frac { { \chi }^{ 2 } }{ \chi } \quad[/LATEX] για καθε [LATEX]\chi \quad \in \Re [/LATEX]να αποδειξετε οτι [LATEX]\lim _{ \chi \rightarrow 0 }{ } \frac { \digamma \left( \chi \right) }{ { \chi }^{ 2 } } =\frac { 1 }{ 2 } [/LATEX]

αν μπορει καποιος ας μου εξηγησει πως απο τη σχεση που μου δινει θα καταφερω να φτιαξω τη σχεση που χρειαζομαι .........

Μηπως στην σχεση πρεπει το χ να ανηκει στο (-οο,-1]U[1,+οο)....γιατι αλλιως δεν εχει νοημα η ποσοτητα στη ριζα!!!!! :hmm:

mary-blackrose · 25-07-12

Αρχική Δημοσίευση από vassilakos:
Μηπως στην σχεση πρεπει το χ να ανηκει στο (-οο,-1]U[1,+οο)....γιατι αλλιως δεν εχει νοημα η ποσοτητα στη ριζα!!!!!

αχχ....χιλια συγνωμη τωρα το ειδα ειχα κανει λαθος στη ριζα και αντι για ριζα (χ^2+1 που ειναι κανονικα) εγραψα χ^2-1.......

OChemist · 26 Ιουλίου 2012

Αρχική Δημοσίευση από mary-blackrose:
καλησπερα θα ηθελα τη βοηθεια σας στην παρακατω ασκηση:
Εστω συναρτηση

Code:

[LATEX]\digamma :\Re \rightarrow \Re [/LATEX] τετοια, ωστε:[LATEX] \digamma \left( \chi \right) +1\ge \sqrt { { \chi }^{ 2 }+1 }[/LATEX], για καθε [LATEX]\chi \quad \in \Re [/LATEX] και [LATEX]\lim _{ \chi \rightarrow 0 }{ \frac { \digamma \left( \chi \right) }{ \chi } =\ell \quad ,\ell \quad \in \Re }[/LATEX] 1) να βρεθει το [LATEX]\ell [/LATEX] Αν: [LATEX]\digamma \left( \chi \right) \le { \digamma }^{ 2 }\left( \chi \right) +\frac { { \chi }^{ 2 } }{ \chi } \quad[/LATEX] για καθε [LATEX]\chi \quad \in \Re [/LATEX]να αποδειξετε οτι [LATEX]\lim _{ \chi \rightarrow 0 }{ } \frac { \digamma \left( \chi \right) }{ { \chi }^{ 2 } } =\frac { 1 }{ 2 } [/LATEX]

αν μπορει καποιος ας μου εξηγησει πως απο τη σχεση που μου δινει θα καταφερω να φτιαξω τη σχεση που χρειαζομαι .........

Λοιπον....δεν υποσχομαι τιποτα...αλλα οριστε τι εκανα...και ΟΠΟΥ με βρισκετε λαθος πειτε μου!!!!
1)Αφου $f(x)+1\geq \sqrt{x^2+1}$ .....τοτε για χ>0:
$\frac{f(x)}{x}\geq \frac{\sqrt{x^2+1}-1}{x}$ ....οποτε..
$\lim_{x\rightarrow 0}\frac{f(x)}{x}=\lim_{x\rightarrow 0} \frac{\sqrt{x^2+1}-1}{x}$ ....
$\lim_{x\rightarrow 0}\frac{f(x)}{x}=\lim_{x\rightarrow 0} \frac{\sqrt{x^2+1}-1}{x}=\lim_{x\rightarrow 0}\frac{x}{\sqrt{x^2+1}+1}=0$ ...
Για χ<0 εχουμε:
$\frac{f(x)}{x}\leq \frac{\sqrt{x^2+1}-1}{x}$ ...οποτε....
$]\lim_{x\rightarrow 0}\frac{f(x)}{x}=\lim_{x\rightarrow 0} \frac{\sqrt{x^2+1}-1}{x}=\lim_{x\rightarrow 0}\frac{x}{\sqrt{x^2+1}+1}=0$ ...Αρα σε καθε περιπτωση..... $\lim_{x\rightarrow 0}\frac{f(x)}{x}=0$ ...και συνεπως l=0....
2)εχουμε οτι $f(x)\leq f^2(x)+\frac{x^2}{2}$ .....οποτε για χ>0
$\frac{f(x)}{x^2}\leq\frac{ f^2(x)}{x^2}+\frac{1}{2}$ ...τοτε
$\lim_{x\rightarrow0}\frac{f(x)}{x^2}=\lim_{x\rightarrow0}\frac{ f^2(x)}{x^2}+\frac{1}{2}$ ...και λογω της (1)..
$\lim_{x\rightarrow0}\frac{f(x)}{x^2}=\lim_{x\rightarrow0}\frac{ f^2(x)}{x^2}+\frac{1}{2}=\frac{1}{2}$
και για χ<0....περνουμε...

...τοτε...
$\lim_{x\rightarrow0}\frac{f(x)}{x^2}=\lim_{x\rightarrow0}\frac{ f^2(x)}{x^2}+\frac{1}{2}$ και λογω παλι της (1)...
$\lim_{x\rightarrow0}\frac{f(x)}{x^2}=\lim_{x\rightarrow0}\frac{ f^2(x)}{x^2}+\frac{1}{2}=\frac{1}{2}$ ....
Οποτε σε καθε περιπτωση $\lim_{x\rightarrow0}\frac{f(x)}{x^2}=\frac{1}{2}$
Αυτααααα....για ΟΠΟΙΑ απορια, διευκρινηση και διορθωση πειτε μου!!!!

Ντίνα951 · 30-07-12

Α.εστω ΖΕC και f(z)= ln/z/ να βρειτε το γεωμετρικο τοπο τω εικονων του z στο μιγαδικο επιπεδο για τον οποιο ισχυει: 1)zf(z)=0 2) f(z)<f(z-i)
Β.Εστω λεR και ο μιγαδικος z δεν ανηκει R για τον οποιο ισχυει λz+z(μιγαδικο)= /z/ 1 να βρειτε τον γεωμετρικο τοπο των εικονων του z για τον οποιο ισχυει η σχεση 1
Γ.να βρειτε τον γεωμετρικο τοπο των εικονων των μιγαδικων z για τουσ οποιους ισχυει
α.z2+z2(μιγαδικος)-4(z+z(μιγαδικος))=2/z/2
β./z/+2im(z)=Re(z)
καμια βοηθεια??? παρακαλω!!!

OChemist · 30-07-12

Αρχική Δημοσίευση από Ντίνα951:
Α.εστω ΖΕC και f(z)= ln/z/ να βρειτε το γεωμετρικο τοπο τω εικονων του z στο μιγαδικο επιπεδο για τον οποιο ισχυει: 1)zf(z)=0 2) f(z)<f(z-i)
Β.Εστω λεR και ο μιγαδικος z δεν ανηκει R για τον οποιο ισχυει λz+z(μιγαδικο)= /z/ 1 να βρειτε τον γεωμετρικο τοπο των εικονων του z για τον οποιο ισχυει η σχεση 1
Γ.να βρειτε τον γεωμετρικο τοπο των εικονων των μιγαδικων z για τουσ οποιους ισχυει
α.z2+z2(μιγαδικος)-4(z+z(μιγαδικος))=2/z/2
β./z/+2im(z)=Re(z)
καμια βοηθεια??? παρακαλω!!!

Ερωτηση η f(z) ειναι ο λογαριθμος του μέτρου του z ή του απολυτου z??? :hmm:

Ντίνα951 · 30-07-12

Αρχική Δημοσίευση από vassilakos:
Ερωτηση η f(z) ειναι ο λογαριθμος του μέτρου του z ή του απολυτου z???

σε ποια ασκηση?

OChemist · 30-07-12

Αρχική Δημοσίευση από Ντίνα951:
σε ποια ασκηση?

Σε αυτη που δινεις...!!!!Μπορεις να το γραψεις σε latex...??Γιατι προσπαθω να καταλαβω περι τεινος προκειτε αλλα....καπου τα χάνω!!!

Ντίνα951 · 30-07-12

Αρχική Δημοσίευση από vassilakos:
Σε αυτη που δινεις...!!!!Μπορεις να το γραψεις σε latex...??Γιατι προσπαθω να καταλαβω περι τεινος προκειτε αλλα....καπου τα χάνω!!!

δν μπορω να τ αωεβασω σε latex... :worry:

απολυτο ειναι αυτο / / και απου βλεπεισ 2 κολλητα με κατι ειναι τετραγωνο! :worry:

OChemist · 30-07-12

Αρχική Δημοσίευση από Ντίνα951:
Α.εστω ΖΕC και f(z)= ln/z/ να βρειτε το γεωμετρικο τοπο τω εικονων του z στο μιγαδικο επιπεδο για τον οποιο ισχυει: 1)zf(z)=0 2) f(z)<f(z-i)
Β.Εστω λεR και ο μιγαδικος z δεν ανηκει R για τον οποιο ισχυει λz+z(μιγαδικο)= /z/ 1 να βρειτε τον γεωμετρικο τοπο των εικονων του z για τον οποιο ισχυει η σχεση 1
Γ.να βρειτε τον γεωμετρικο τοπο των εικονων των μιγαδικων z για τουσ οποιους ισχυει
α.z2+z2(μιγαδικος)-4(z+z(μιγαδικος))=2/z/2
β./z/+2im(z)=Re(z)
καμια βοηθεια??? παρακαλω!!!

αυτα μπορεις να μου εξηγησεις τι λένε...????

Ντίνα951 · 30-07-12

λz+z(μιγαδικο)= /z/ 1 το δευτερο ζ ειναι μιγαδικοσ /z/ απολυτο και αυτη ειναι η σχεση 1

.z2+z2(μιγαδικος)-4(z+z(μιγαδικος))=2/z/2 z στο τετραγωνο + z μιγαδικος και στο τετραγωνο - 4 (z+z) το δευτερο z ειναι μιγαδικος =2 απολυτο z στο τετραγωνο

OChemist · 30-07-12

Αρχική Δημοσίευση από Ντίνα951:
Α.εστω ΖΕC και f(z)= ln/z/ να βρειτε το γεωμετρικο τοπο τω εικονων του z στο μιγαδικο επιπεδο για τον οποιο ισχυει: 1)zf(z)=0 2) f(z)<f(z-i)
Β.Εστω λεR και ο μιγαδικος z δεν ανηκει R για τον οποιο ισχυει λz+z(μιγαδικο)= /z/ 1 να βρειτε τον γεωμετρικο τοπο των εικονων του z για τον οποιο ισχυει η σχεση 1
Γ.να βρειτε τον γεωμετρικο τοπο των εικονων των μιγαδικων z για τουσ οποιους ισχυει
α.z2+z2(μιγαδικος)-4(z+z(μιγαδικος))=2/z/2
β./z/+2im(z)=Re(z)
καμια βοηθεια??? παρακαλω!!!

Μισο λεπτο.....πες μου αν την εγραψα σωστα:
=>A) Εστω $z\epsilon R$ με $f(z)=ln\left|z \right|$ .....να βρειτε το γεωμετρικο τοπο τω εικονων του z στο μιγαδικο επιπεδο για τον οποιο ισχυει:
i) $zf(z)=0$
ii) $f(z)<f(z-i)$
B)Εστω $\lambda \epsilon R$ και ο μιγαδικος $z\neq R$ για τον οποιο ισχυει : $\lambda z+\bar{z}=\left|z \right|$ (1).... να βρειτε τον γεωμετρικο τοπο των εικονων του z για τον οποιο ισχυει η σχεση (1)
Γ) Nα βρειτε τον γεωμετρικο τοπο των εικονων των μιγαδικων z για τουσ οποιους ισχυει :
i) $z^2+\bar{z}^2-4(z+\bar{z})=2\left|z \right|^2$
ii) $\left|z \right|+2Im(z)=Re(z)$
πες μου εαν αυτα εννοεις...!!!! :hmm:

Ντίνα951 · 30-07-12

Αρχική Δημοσίευση από vassilakos:
Μισο λεπτο.....πες μου αν την εγραψα σωστα:
=>A) Εστω $z\epsilon R$ με $f(z)=ln\left|z \right|$ .....να βρειτε το γεωμετρικο τοπο τω εικονων του z στο μιγαδικο επιπεδο για τον οποιο ισχυει:
i) $zf(z)=0$
ii) $f(z)<f(z-i)$
B)Εστω $\lambda \epsilon R$ και ο μιγαδικος $z\neq R$ για τον οποιο ισχυει : $\lambda z+\bar{z}=\left|z \right|$ (1).... να βρειτε τον γεωμετρικο τοπο των εικονων του z για τον οποιο ισχυει η σχεση (1)
Γ) Nα βρειτε τον γεωμετρικο τοπο των εικονων των μιγαδικων z για τουσ οποιους ισχυει :
i) $z^2+\bar{z}^2-4(z+\bar{z})=2\left|z \right|^2$
ii) $\left|z \right|+2Im(z)=Re(z)$
πες μου εαν αυτα εννοεις...!!!!

ολοσωστα!! :clapup:

OChemist · 30-07-12

Αρχική Δημοσίευση από Ντίνα951:
ολοσωστα!!

οκ...λεω και εγω τι ηταν αυτο το z(μιγαδικος)...!!!!

Ντίνα951 · 30-07-12

Αρχική Δημοσίευση από vassilakos:
οκ...λεω και εγω τι ηταν αυτο το z(μιγαδικος)...!!!!

χεχεχεχε!!!!!!!!!!!!!!!!! :redface:

Ντίνα951 · 30-07-12

πάντως σε ευχαριστώ πολύ που ασχολείσαι !!

OChemist · 30-07-12

Αρχική Δημοσίευση από Ντίνα951:
πάντως σε ευχαριστώ πολύ που ασχολείσαι !!
=>A) Εστω $z\epsilon R$ με $f(z)=ln\left|z \right|$ .....να βρειτε το γεωμετρικο τοπο τω εικονων του z στο μιγαδικο επιπεδο για τον οποιο ισχυει:
i) $zf(z)=0$
ii) $f(z)<f(z-i)$
B)Εστω $\lambda \epsilon R$ και ο μιγαδικος $z\neq R$ για τον οποιο ισχυει : $\lambda z+\bar{z}=\left|z \right|$ (1).... να βρειτε τον γεωμετρικο τοπο των εικονων του z για τον οποιο ισχυει η σχεση (1)
Γ) Nα βρειτε τον γεωμετρικο τοπο των εικονων των μιγαδικων z για τουσ οποιους ισχυει :
i) $z^2+\bar{z}^2-4(z+\bar{z})=2\left|z \right|^2$
ii) $\left|z \right|+2Im(z)=Re(z)$

Λοιπον εχουμε:
A) i)αν $zf(z)=0\Leftrightarrow zln\left|z \right|=0$ τοτε $z=0$ ή $ln\left|z \right|=0$ ...οποτε ειτε ο Γ.Τ των εικονων του z ειναι απλως το σημειο Ο(0,0), αφου z=0, ειτε ειναι ο μοναδιαιος κυκλος αφου $ln\left|z \right|=0\Leftrightarrow \left|z \right|=1$

ii) $f(z)<f(z-i)\Leftrightarrow ln\left|z \right|<ln\left|z-i \right|$ ...και επειδη η lnχ ειναι γνησιως αυξουσα τοτε $\left|z \right|<\left|z-i \right|$ οποτε αν θεσουμε z=χ+yi ,με $x ,y\epsilon R$ τοτε κανοντας τις πραξεις θα προκυψει οτι ο y<1/2 δηλαδη ο Γ.Τ των εικονων του z ειναι το ημιεπιπεδο που οριζετε απο την ευθεια y=1/2 και κατω

Β)Εχουμε οτι $\lambda z+\bar{z}=\left|z \right|$ ..(1)...οποτε αν υποθεσουμε οτι $w=\lambda z+\bar{z}$ και επειδη $\left|z \right|\epsilon R$ τοτε και $w\epsilon R$ αρα και $\bar{w}\epsilon R$ οποτε θα εχουμε οτι και
$\lambda \bar{z}+z=\left|z \right|$ ..(2)....αρα πρεπει (1)=(2)<=> $\lambda \bar{z}+z=\lambda z+\bar{z}$ ...οποτε για $\lambda \epsilon R-[1]$ .... $z(\lambda -1)=\bar{z}(\lambda -1)\Leftrightarrow z=\bar{z}$ ....αρα $z\epsilon R$ (ατοπο απο υποθεση).....Αρα υποχρεωτικα το λ=1 αρα στην (1) $z+\bar{z}=\left|z\right|$ ...αρα αν θεσεις z=x+yi, με $x ,y\epsilon R$ τοτε θα προκυψει οτι $y^2=3x^2\Leftrightarrow y=\pm \sqrt{3}x$ ...οποτε ο Γ.Τ των εικονων τουz ειναι η ευθεια (ε): $y=\sqrt{3}x$ ....ή....(ε): $y=-\sqrt{3}x$

Γ) i)Εχουμε οτι $z^2+\bar{z}^2-4(z+\bar{z})=2\left|z \right|^2$ ....αρα αν θεσεις z=x+yi, με $x ,y\epsilon R$ και κανεις τις πραξεις τοτε θα προκυψει οτι : $y^2=-2x$ ....Αρα ο Γ.Τ των εικονων του z ανηκουν στην παραβολη (C): $y^2=-2x$ .....με εστια το Ε(-1/2,0) και διευθετουσα την $x=1/2$

ii) Εχουμε οτι $\left|z \right|+2Im(z)=Re(z)$ ....αρα αν θεσεις z=x+yi, με $x ,y\epsilon R$ και κανεις τις πραξεις τοτε θα προκυψει οτι : $3y^2=4xy\Leftrightarrow y(3y-4x)=0$ ...αρα ειτε $y=0$ ....δηλαδη ο Γ.Τ των εικονων του z ειναι ο χ'χ, ειτε $y=\frac{4x}{3}$ ....δηλαδη ο Γ.Τ των εικονων του z ειναι η ευθεια (ε): $y=\frac{4x}{3}$
Αυτααα.....για ΟΠΟΙΑ απορια ρωτα με...!!!!

Ντίνα951 · 30-07-12

Αρχική Δημοσίευση από vassilakos:
Λοιπον εχουμε:
A) i)αν $zf(z)=0\Leftrightarrow zln\left|z \right|=0$ τοτε $z=0$ ή $ln\left|z \right|=0$ ...οποτε ειτε ο Γ.Τ των εικονων του z ειναι απλως το σημειο Ο(0,0), αφου z=0, ειτε ειναι ο μοναδιαιος κυκλος αφου $ln\left|z \right|=0\Leftrightarrow \left|z \right|=1$

ii) $f(z)<f(z-i)\Leftrightarrow ln\left|z \right|<ln\left|z-i \right|$ ...και επειδη η lnχ ειναι γνησιως αυξουσα τοτε $\left|z \right|<\left|z-i \right|$ οποτε αν θεσουμε z=χ+yi ,με $x ,y\epsilon R$ τοτε κανοντας τις πραξεις θα προκυψει οτι ο y<1/2 δηλαδη ο Γ.Τ των εικονων του z ειναι το ημιεπιπεδο που οριζετε απο την ευθεια y=1/2 και κατω

Β)Εχουμε οτι $\lambda z+\bar{z}=\left|z \right|$ ..(1)...οποτε αν υποθεσουμε οτι $w=\lambda z+\bar{z}$ και επειδη $\left|z \right|\epsilon R$ τοτε και $w\epsilon R$ αρα και $\bar{w}\epsilon R$ οποτε θα εχουμε οτι και
$\lambda \bar{z}+z=\left|z \right|$ ..(2)....αρα πρεπει (1)=(2)<=> $\lambda \bar{z}+z=\lambda z+\bar{z}$ ...οποτε για $\lambda \epsilon R-[1]$ .... $z(\lambda -1)=\bar{z}(\lambda -1)\Leftrightarrow z=\bar{z}$ ....αρα $z\epsilon R$ (ατοπο απο υποθεση).....Αρα υποχρεωτικα το λ=1 αρα στην (1) $z+\bar{z}=\left|z\right|$ ...αρα αν θεσεις z=x+yi, με $x ,y\epsilon R$ τοτε θα προκυψει οτι $y^2=3x^2\Leftrightarrow y=\pm \sqrt{3}x$ ...οποτε ο Γ.Τ των εικονων τουz ειναι η ευθεια (ε): $y=\sqrt{3}x$ ....ή....(ε): $y=-\sqrt{3}x$

Γ) i)Εχουμε οτι $z^2+\bar{z}^2-4(z+\bar{z})=2\left|z \right|^2$ ....αρα αν θεσεις z=x+yi, με $x ,y\epsilon R$ και κανεις τις πραξεις τοτε θα προκυψει οτι : $y^2=-2x$ ....Αρα ο Γ.Τ των εικονων του z ανηκουν στην παραβολη (C): $y^2=-2x$ .....με εστια το Ε(-1/2,0) και διευθετουσα την $x=1/2$

ii) Εχουμε οτι $\left|z \right|+2Im(z)=Re(z)$ ....αρα αν θεσεις z=x+yi, με $x ,y\epsilon R$ και κανεις τις πραξεις τοτε θα προκυψει οτι : $3y^2=4xy\Leftrightarrow y(3y-4x)=0$ ...αρα ειτε $y=0$ ....δηλαδη ο Γ.Τ των εικονων του z ειναι ο χ'χ, ειτε $y=\frac{3x}{4}$ ....δηλαδη ο Γ.Τ των εικονων του z ειναι η ευθεια (ε): $y=\frac{3x}{4}$
Αυτααα.....για ΟΠΟΙΑ απορια ρωτα με...!!!!

Σε ευχαριστω παρα πολυ!!!! :clapup:

Να εισαι καλα!!

OChemist · 30-07-12

Αρχική Δημοσίευση από Ντίνα951:
Σε ευχαριστω παρα πολυ!!!! Να εισαι καλα!!

Τιποτα....Αλιμονο....Ευχαριστηση μου!!!! :redface:

*Serena* · 30-07-12

Λίγη βοήθεια κάποιος!

Αν η εικόνα του μιγαδικού ζ κινειται στην ευθεία ψ=χ να δειξετε οτι η εικόνα του ω=ζ+1/ζ κινείται σε μια ισοσκελή υπερβολή.
και
Εστω η συνάρτηση f για την οποία ισχύει f(f(x))=3x+4 για κάθε χ ανήκει R.
Να δείξετε ότι f(3x+4)=3f(x)+4
Να υπολογίσετε το f(-2)

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Τιμώμενο Μέλος