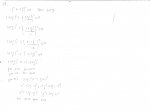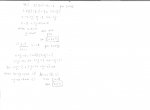lenbias
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Litle Prince
Νεοφερμένο μέλος


αν μπορουσες να κανεις λιγο τον κοπο θα το εκτιμουσα πολυ

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lenbias
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Litle Prince
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lenbias
Εκκολαπτόμενο μέλος
Litle Prince
Νεοφερμένο μέλος



αν δεν βαριεσαι κανε και τις αλλες ολο το βραδυ εχουμε


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lenbias
Εκκολαπτόμενο μέλος
Litle Prince
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lenbias
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Dias
Επιφανές μέλος


Και σε τι θα σε ωφελήσει να πας στο φροντιστήριο σου τις ασκήσεις λυμένες από κάποιον άλλο? Το θέμα είναι να τις λύσεις μονος σου. Το βιβλίο σου έχει και ασκήσεις λυμένες πριν. Δες πώς τις λύνει και προσπάθησε αυτές που θέλεις. Η δική σου δουλειά έχει αξία.αν δεν βαριεσαι κανε και τις αλλες ολο το βραδυ εχουμε
- Να και μια άλλη λύση για την 1η, γιατί συνήθως οι καθηγητές τις λύσεις με z=x+yi τις σνομπάρουνε.
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lenbias
Εκκολαπτόμενο μέλος
Saito
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Chemwizard
Τιμώμενο Μέλος


 Λογικα εκεινος μπορει να σε βοηθησει καλυτερα απο εμενα.
Λογικα εκεινος μπορει να σε βοηθησει καλυτερα απο εμενα.Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Θανάσης Χανιά
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Δεν ξέρω αν κατάλαβες...
Δηλαδή αποδεικνύεις κάτι αρχίζοντας από κάτι σαν αυταπόδεικτη υπόθεση ή απλή υπόθεση
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
woochoogirl
Τιμώμενο Μέλος


Without loss of generality (abbreviated to WLOG; less commonly stated as without any loss of generality or with no loss of generality) is a frequently used expression in mathematics. The term is used before an assumption in a proof which narrows the premise to some special case; it is implied that the proof on this subset can be easily applied to all others (or that all other cases are trivial). Thus, given a proof of the special case, it is trivial to show that the conclusions follow from the full premise.
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
kostasrousmath
Εκκολαπτόμενο μέλος


Φίλε Γιάννη....kostas-rous-math.....Στη στατιστικη,ή σε μερικα άλλα πεδία,μερικές φορες κανει καποιος μια υποθεση για κατι,την οποια ανάγει σε ενα γενικοτερο σύνολο.Για να ισχυει ομως η τελευταία,δεν πρεπει να ακυρώνει κάτι που ισχύει γενικά.Δεν είναι ούτε το αντικειμενο μου,ούτε μπορώ να το εξηγήσω και τέλεια.Που ειναι ο φιλος ο kostourasmath τωρα που τον θέλω?Λογικα εκεινος μπορει να σε βοηθησει καλυτερα απο εμενα.


Παραταύτα, έχει δίκιο ο Γιάννης, φίλε Saito....

Επίσης, χρησιμοποιείται και με άλλη εννοια....
Για να καταλάβεις, παραθέτω μια άσκηση...
Έστω ότι η 2η παράγωγος μιας συνάρτησης





Η άσκηση είναι θέμα πανελληνίων και σε μερικούς τρόπους λύσης δεν απαιτείται η συνέχεια της

Την βάζω όμως εδώ επειδή έχει μεγάλη ποικιλία λύσεων πχ
1)Μόνο με Rolle+θεώρημα ενδιαμέσων τιμών
2)Μόνο με ΘΜΤ+Bolzano+Rolle
3)Μόνο με ΘΜΤ+Bolzano
4)Μόνο με Fermat+Rolle
5)Μόνο με ΘΜΤ+μονοτονία+Bolzano και την εις άτοπο απαγωγή
6)με κυρτότητα χρησιμοποιώντας το λήμμα ὀτι η κλίση των χορδών με ένα άκρο σταθερό είναι αύξουσα
7)με κυρτότητα χρησιμοποιώντας το λήμμα ὀτι δεν υπάρχουν τρια συνευθειακά σημεία στην

Θα δώσω τις λύσεις σε συνημμένο αργότερα ΑΛΛΑ ΘΑ ΗΤΑΝ ΩΡΑΙΟ ΝΟΜΙΖΩ ΝΑ ΒΡΕΘΟΥΝ ΚΑΙ ΑΛΛΕΣ ΛΥΣΕΙΣ
Απάντηση:
Λόγω της δοθείσας η f αποκλείεται να είναι σταθερή στο [a,d]. Λόγω της συνέχειας της f στο [a,d]
προκύπτει πως αυτή παρουσιάζει μέγιστη κι ελάχιστη τιμή έστω στα



το οποίο δίνει


Υ.Γ. Χωρις βλάβη της γενικότητας υπέθεσα
Στο Υ.Γ. θα μπορούσα κάλιστα να υποθέσω, αντί
(σσσσ την βρήκα σε ενα site, παραταύτα μας της είχαν βάλει και εμας στο πρώτο εξάμηνο)
Μπες και εδώ...
https://wo-log.blogspot.com/2009/10/blog-post_17.html
Πάντως δεν είναι κάτι το εξαιρετικά δύσκολο αυτή η "βλάβη της γενικότητας"...Μην κολλάς σε φράσεις...
Τα μαθηματικά έχουν απειρους τρόπους να πεις και να λύσεις την ίδια άσκηση (βλεπεις και παραπάνω με πόσους τρόπους λύνεται), αυτό το μαθαίνεις με την εξάσκηση και την ενασχόληση....(και εγώ δεν ξέρω σχεδόν τίποτα
 ...)
...)Δες και αυτό...
https://el.wikipedia.org/wiki/%CE%98%CE%B5%CE%BC%CE%B5%CE%BB%CE%B9%CF%8E%CE%B4%CE%B5%CF%82_%CE%B8%CE%B5%CF%8E%CF%81%CE%B7%CE%BC%CE%B1_%CE%B1%CF%81%CE%B9%CE%B8%CE%BC%CE%B7%CF%84%CE%B9%CE%BA%CE%AE%CF%82
Σε κάποιο σημείο λέει:
" o qj είναι πρώτος, p1 = qj. Χωρίς βλάβη της γενικότητας μπορούμε να υποθέσουμε ότι qj = q1..."
Δηλαδή, μπορούμε να αλλάξουμε την "σειρά" όπως γράφουμε τα μέλη στην ισότητα, χωρίς να αλλάξει το αποτέλεσμα...
Που είναι προφανές ότι μπορεί να γίνει....
Προσωπικά την "βλαβη της γενικότητας" την θεωρώ μαμακία,αλλά τεσπα....
Αν δεν κατάλαβες ή ακόμη αν θες όποια βοήθεια στα μαθηματικά στείλε pm...
Φιλικά Κωνσταντίνος.....
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Saito
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
red span
Δραστήριο μέλος


Παρακαλω βοηθεια!
Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
leobakagian
Εκκολαπτόμενο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 5 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki