Έχουμε
(2+sin\phi -icos\phi) }=\frac{2+sin\phi -icos\phi}{{(2+sin\phi)}^{2}+{cos}^{2}\phi}=\frac{2+sin\phi}{5+4sin\phi}-\frac{cos\phi}{5+4sin\phi}i=x+yi)
όπου
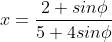
και
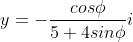
Θα εξεταστεί στη συνέχεια αν οι εικόνες του μιγαδικού z ανήκουν σε κύκλο και αν ναι θα προσδιοριστεί το κέντρο και η ακτίν ατου. Αντικαθιστούμε αυτές τις εκφράσεις των x και y σε εξίσωση της μορφής
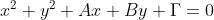
όπου Α,Β,Γ προσδιοριστέοι συντελεστές. Μετά από πράξεις, η παραπάνω εξίσωση αποκτά την μορφή:
sin\varphi -Bcos\varphi +2A+5\Gamma +1=0)
Για να ισχύει η εξίσωση αυτή για κάθε
)
(ή R ή οποιοδήποτε σύνολο του φ καθορίζεται από την εκφώνιση αλλά συνήθως είναι το [0,2π)) τότε πρέπει να ισχύουν οι εξής συνθήκες:
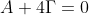
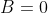
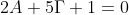
Από την λύση του παραπάνω συστήματος προκύπτουν
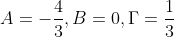
Συνεπώς η εξίσωση γράφεται στην μορφή
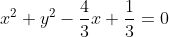
Παρατηρούμε ότι
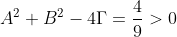
που σημαίνει ότι η εξίσωση αυτή παριστάνει κύκλο. Το κέντρο του κύκλου
)
έχει συντεταγμένες

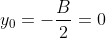
και ακτίνα
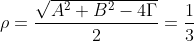
Συνεπώς οι εικόνες των μιγαδικών z ανήκουν σε κύκλο κέντρου
)
και ακτίνας
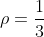
με εξίσωση
}^{2}+{y}^{2}=\frac{1}{9})
Δηλαδή για τους μιγαδικούς z ισχύει
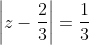
[/quote]
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


πολυ ευκολα θα την παταγα!
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki





