Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[Μάρκος Βασίλης]

Και εγώ μέχρι σήμερα θυμόμουν οτι το βιβλίο τα είχε ως δυο διαφορετικές περιπτώσεις ενώ επι της ουσίας , κοιτάζοντας την σχετική θεωρία πάλι σήμερα , παρατήρησα οτι η οριζόντια είναι απλά μια εκφυλισμένη περίπτωση της πλάγιας . Προσωπικά θα προτιμούσα αυτή την ερμηνεία,τώρα εαν κάποιος θέλει να τα αντιμετωπίζει διαφορετικά αυτά τα δύο οτι τον βολεύει καλύτερα υποθέτω,ωστόσο είναι τα ίδια πράγματα .

Ο σκοπός του βιβλίου είναι καθαρά διδακτικός - και καλά κάνει. Η μόνη συνάρτηση για την οποία γνωρίζουν a priori ότι έχει ασυμπτωτική συμπεριφορά στα άπειρα είναι η 1/χ, η οποία έχει οριζόντια ασύμπτωτη τον άξονα των χ - και στα δύο άπειρα. Από εκεί, παρατηρώντας τη, γενικεύεται αυτή η συμπεριφορά σε κάθε κλίση. Τυπικά μιλώντας, η έννοια τη ασύμπτωτης εισάγεται και στην Β' λυκείου με τις υπερβολές, αλλά πια δεν είναι στη διδακτέα ύλη - επί του πρακτέου, ό,τι κι αν έλεγε το υπουργείο, ποτέ δε δινόταν έμφαση στις ασύμπτωτες υπερβολής τα τελευταία χρόνια.

 

[Samael]

Ο σκοπός του βιβλίου είναι καθαρά διδακτικός - και καλά κάνει. Η μόνη συνάρτηση για την οποία γνωρίζουν a priori ότι έχει ασυμπτωτική συμπεριφορά στα άπειρα είναι η 1/χ, η οποία έχει οριζόντια ασύμπτωτη τον άξονα των χ - και στα δύο άπειρα. Από εκεί, παρατηρώντας τη, γενικεύεται αυτή η συμπεριφορά σε κάθε κλίση. Τυπικά μιλώντας, η έννοια τη ασύμπτωτης εισάγεται και στην Β' λυκείου με τις υπερβολές, αλλά πια δεν είναι στη διδακτέα ύλη - επί του πρακτέου, ό,τι κι αν έλεγε το υπουργείο, ποτέ δε δινόταν έμφαση στις ασύμπτωτες υπερβολής τα τελευταία χρόνια.

Σίγουρα καλά κάνουν,εφόσον έρχεται πιο εύκολα στον νου ο διαχωρισμός . Πρέπει να έχεις δίκιο,θυμάμαι αμυδρά οτι στην υπερβολή έλεγε κάτι για ασύμπτωτες . Ευτυχώς δεν είναι τίποτα το τρομερό και η εισαγωγή στο θέμα στην Γ λυκείου δεν επηρεάζει την ικανότητα της κατανόησης του μαθητή .Οι κωνικές τομές είναι ένα πονεμένο θέμα γενικά . Ακολουθούμε εννοείται το σχολικό βιβλίο πάντα καθώς οι εξεταστές διορθώνουν βάσει αυτού . Όποιος μπορεί να διαβάσει την υπερβολή ωστόσο το συνιστώ,γιατί εαν και εκτός ύλης,στην κυματική,στην φυσική της γ λυκείου ,εμφανίζεται ως λύση στο πρόβλημα της συμβολής απο διάδοση δύο επιφανειακών κυμάτων ,οπότε δεν βλάπτει να έχει κανείς μια στοιχειώδη γνώση για περί τίνος πρόκειται .

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 20 Μαρτίου 2020

Ευχαριστώ πάρα πολύ, ήσουν κατατοπιστικότατος και ξεκαθάρισα (νομίζω) αρκετά πράγματα. Και πάλι ευχαριστώ

Χαίρομαι τότε ,καλό διάβασμα .

 

[Panos_02]

γεια
θα ήθελα να ρωτήσω από το 3.1 το αόριστο ολοκλήρωμα το κάνατε ή όχι;

 

[Μάρκος Βασίλης]

γεια
θα ήθελα να ρωτήσω από το 3.1 το αόριστο ολοκλήρωμα το κάνατε ή όχι;

Το αόριστο ολοκλήρωμα είναι εκτός ύλης με τη μορφή του και αντί για τον πίνακα αορίστων ολοκληρωμάτων που δίνεται στο σχολικό βιβλίο δίνεται ο αντίστοιχος πίνακας παραγουσών/αρχικών συναρτήσεων. Επομένως, το μόνο που κρατάτε είναι ο πίνακας με τις αρχικές και η έννοια της αντιπαραγώγισης.

 

[kvstas92]

Καλησπερα φιλοι, ειμαι καινουργιος στην κοινοτητα και θα ηθελα να μου πειτε την αποψη σας για την παρακατω λυση. Δεν ειμαι σιγουρος αν ειναι σωστη η αν δεν ειναι σωστη

 

[Samael]

Καλησπερα φιλοι, ειμαι καινουργιος στην κοινοτητα και θα ηθελα να μου πειτε την αποψη σας για την παρακατω λυση. Δεν ειμαι σιγουρος αν ειναι σωστη η αν δεν ειναι σωστη

Δεν βλέπω πως αιτιολογείς την απαίτηση f(ω) = 0.
@Μάρκος Βασίλης εσένα πως σου φαίνεται ;

Παρακάτω παραθέτω μια ακόμα προσέγγιση :

f(f(x)) + f³(x) = 2x+8

Θέτω όπου x το f-1(x) στην παραπάνω σχέση και έχω :

f(f(f-1(x) ) ) + f³(f-1(x) ) = 2f-1(x) +8
f(x) + f³(f-1(x) ) = 2f-1(x) + 8
f(x) + [f(f-1(x) )]³ = 2f-1(x) + 8
f(x) + x³ = 2f-1(x) + 8

Για x=2 στην παραπάνω :

f(2) + 8 = 2f-1(2) + 8
f(2) - 2f-1(2) = 0

Σύμφωνα με την παραπάνω και την δεύτερη δοθείσα σχέση :

f(g(x)-x) - f(lnx+1) = 2f-1(2) - f(2) = 0
f(g(x) - x) = f(lnx+1) <=> f: 1-1
g(x) - x = lnx+1
g(x) = x+lnx+1 , x>0

 

[kvstas92]

Δεν βλέπω πως αιτιολογείς την απαίτηση f(ω) = 0.
@Μάρκος Βασίλης εσένα πως σου φαίνεται ;

Παρακάτω παραθέτω μια ακόμα προσέγγιση :

f(f(x)) + f³(x) = 2x+8

Θέτω όπου x το f-1(x) στην παραπάνω σχέση και έχω :

f(f(f-1(x) ) ) + f³(f-1(x) ) = 2f-1(x) +8
f(x) + f³(f-1(x) ) = 2f-1(x) + 8
f(x) + [f(f-1(x) )]³ = 2f-1(x) + 8
f(x) + x³ = 2f-1(x) + 8

Για x=2 στην παραπάνω :

f(2) + 8 = 2f-1(2) + 8
f(2) - 2f-1(2) = 0

Σύμφωνα με την παραπάνω και την δεύτερη δοθείσα σχέση :

f(g(x)-x) - f(lnx+1) = 2f-1(2) - f(2) = 0
f(g(x) - x) = f(lnx+1) <=> f: 1-1
g(x) - x = lnx+1
g(x) = x+lnx+1 , x>0

ουσιαστικα ειπα πως η f(ω) oπου ειναι η f(f(0)) ειναι μηδεν αν και μονο αν 8-f(0)^3=0 ελυσα και βρηκα οτι το f(0)=2 αρα ειπα πως και το f(f(0))=0
υστερα εβαλα στο 2f-1(2) το f(0) που κανει μηδεν και στο f(2) οπου 2 το f(0) που βρηκα οτι κανει 0
δεν ξερω κατα ποσο ειναι σωστο...

 

[Samael]

ουσιαστικα ειπα πως η f(ω) oπου ειναι η f(f(0)) ειναι μηδεν αν και μονο αν 8-f(0)^3=0 ελυσα και βρηκα οτι το f(0)=2 αρα ειπα πως και το f(f(0))=0
υστερα εβαλα στο 2f-1(2) το f(0) που κανει μηδεν και στο f(2) οπου 2 το f(0) που βρηκα οτι κανει 0
δεν ξερω κατα ποσο ειναι σωστο...

Το πρόβλημα είναι οτι δέχεσαι αυτό που θες να αποδείξεις κατά κάποιον τρόπο εδώ .
Γι'αυτό μεν η προσέγγιση σου είναι καλή,διότι διαισθητικά ξέρεις τι πρέπει να δείξεις,ωστόσο για να είσαι απο άποψη μαθηματικών σωστός, οφείλεις να αποδείξεις αυτή την υποψία κάνοντας αντικειμενικές υποθέσεις που ξέρεις ή μπορείς να δείξεις οτι ισχύουν . Σε αυτή την περίπτωση μπορεί να μην φαίνεται τόσο σπουδαίο γιατί σου είναι προφανές το τι πρέπει να κάνεις , αλλά σε μεγαλύτερα προβλήματα μπορείς να μπλέξεις άσχημα, καθώς εκεί η διαίσθηση βοηθάει όλο και λιγότερο .

 

[kvstas92]

Το πρόβλημα είναι οτι δέχεσαι αυτό που θες να αποδείξεις κατά κάποιον τρόπο εδώ .
Γι'αυτό μεν η προσέγγιση σου είναι καλή,διότι διαισθητικά ξέρεις τι πρέπει να δείξεις,ωστόσο για να είσαι απο άποψη μαθηματικών σωστός, οφείλεις να αποδείξεις αυτή την υποψία κάνοντας αντικειμενικές υποθέσεις που ξέρεις ή μπορείς να δείξεις οτι ισχύουν . Σε αυτή την περίπτωση μπορεί να μην φαίνεται τόσο σπουδαίο γιατί σου είναι προφανές το τι πρέπει να κάνεις , αλλά σε μεγαλύτερα προβλήματα μπορείς να μπλέξεις άσχημα, καθώς εκεί η διαίσθηση βοηθάει όλο και λιγότερο .

το συγκεκριμενο ηταν υποερωτημα απο ενα διαγωνισμα σε θεμα β και δεν επιανε τοσο πολυ. Δεν πολυ ασχοληθηκα πανω σαυτο γιατι δεν μου ηρθε στο μυαλο να θεσω οπου χ το φ-1(χ). Ευχαριστω παντως

 

[Samael]

το συγκεκριμενο ηταν υποερωτημα απο ενα διαγωνισμα σε θεμα β και δεν επιανε τοσο πολυ. Δεν πολυ ασχοληθηκα πανω σαυτο γιατι δεν μου ηρθε στο μυαλο να θεσω οπου χ το φ-1(χ). Ευχαριστω παντως

Σκοπός σου πρέπει να είναι να παίρνεις όσες περισσότερες μονάδες είναι δυνατόν γιατί δεν ξέρεις απο που μπορείς να χάσεις,ή να σκαλώσεις την ώρα των εξετάσεων . Οπότε έτσι μεγιστοποιείς την πιθανότητα να τα πας καλά . Ωστόσο το σημαντικό είναι να προσέχεις τέτοιες λεπτομέρειες γιατί εαν και μπορεί να μην πιάνουν πολλά,σου καταστρέφουν την συνέχεια σε πιο περίπλοκα θέματα(3ο,4ο) .

Σαν γενικό κανόνα ,όταν κάνεις μια απόδειξη, είναι καλό να προσπαθείς ο ίδιος να της "επιτεθείς" . Ρώτα δηλαδή τι μπορεί να πάει στραβά και που,πως και γιατί ; Εαν ο ίδιος βρίσκεις ψεγάδια ή σημεία που δεν είναι επαρκώς αιτιολογημένα ή δεν μπορείς να εξηγήσεις με πλήρη σαφήνεια, τότε υπάρχει μεγάλη πιθανότητα να έχεις λάθος ή να μην είναι η καλύτερη απόδειξη που θα μπορούσες να κάνεις(έχει περιττές υποθέσεις ή αοριστίες) .

Εύχομαι καλό διάβασμα .

 

[Μάρκος Βασίλης]

Καλησπερα φιλοι, ειμαι καινουργιος στην κοινοτητα και θα ηθελα να μου πειτε την αποψη σας για την παρακατω λυση. Δεν ειμαι σιγουρος αν ειναι σωστη η αν δεν ειναι σωστη

Γενικά, κράτα τη λύση του @Samael, καθώς είναι σωστή. Αυτό που εσύ έχεις αποδείξει, όπως είπες και μόνος σου, είναι ότι «f(f(0))=0 αν και μόνον αν f(0)=2». Ωστόσο, αυτό δε σημαίνει ότι ισχύει κάτι από τα δύο, απλά, όταν ένα από τα δύο ισχύει τότε (και μόνον τότε) ισχύει και το άλλο. Επομένως, δεν μπορείς να ισχυριστείς ότι f(0)=2 «ελαφρά τη καρδία».

Για λόγους πληρότητας, να δώσω κι άλλη μία λύση εδώ - όλες παραλλαγές της ίδιας ιδέας είναι, βέβαια. Αρχικά, αφού η f είναι «1-1» - άρα και αντιστρέψιμη - μπορούμε να την εφαρμόζουμε σε ισότητες χωρίς «φόβο» - με ισοδυναμίες, δηλαδή. Ξεκινάμε, λοιπόν, από το να αλλάξουμε λίγο το ζητούμενο:

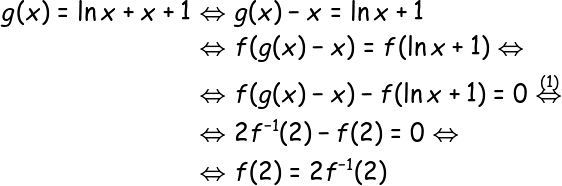
Αρκεί, επομένως, να δείξουμε ότι

. Αυτό είναι εύκολο τώρα, αφού, θέτοντας στην αρχική ισότητα όπου x το

παίρνουμε, διαδοχικά:

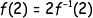
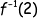
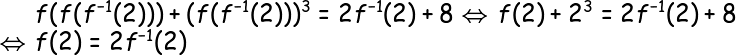
οπότε και ξεμπερδέψαμε.

Γενικά, πέρα από το να ξεκινάς από τις υποθέσεις και να προσπαθείς να παραγάγεις το αποτέλεσμα που θες, μπορείς πρώτα να ξεκινάς και:

1. είτε να αναδιατυπώνεις το ζητούμενο, όπως εδώ, σε μία πιο απλή μορφή,
2. είτε να υποθέτεις (στο πρόχειρο) ότι ισχύει το ζητούμενο και να καταλήγεις σε κάποιες λογικές συνέπειες που έχει αυτό (είναι λίγο γενικότερο από το πρώτο αυτό, μιας και δεν προχωράς απαραίτητα με λογικές ισοδυναμίες).

Αυτό που κερδίζεις είναι ότι, στη χειρότερη περίπτωση, έχεις μία καλύτερη εικόνα του προβλήματος - στην καλύτερη, έχεις μία απλούστερη μορφή, όπως σε αυτήν την περίπτωση.

 

[aggelosst9]

Πριν 10 λεπτά τέλειωσα διαγώνισμα στο διαφορικό λογισμό και στο Θέμα Γ τα σκ@τωσ@ με συγχωρείτε για την έκφραση :p. Παραθέτω και αν θέλετε πείτε μου τις απόψεις σας για τη λύση που θ γράφατε.

Μόνο την εφαπτομένη βρήκα και πείτε μου ότι φ'(1)=-1/3 αλλιώς θα φαρμακωθώ

 

[Μάρκος Βασίλης]

Πριν 10 λεπτά τέλειωσα διαγώνισμα στο διαφορικό λογισμό και στο Θέμα Γ τα σκ@τωσ@ με συγχωρείτε για την έκφραση :p. Παραθέτω και αν θέλετε πείτε μου τις απόψεις σας για τη λύση που θ γράφατε.

Μόνο την εφαπτομένη βρήκα και πείτε μου ότι φ'(1)=-1/3 αλλιώς θα φαρμακωθώ

Κοίτα, το πρώτο ερώτημα είναι "σχεδόν" άσκηση του σχολικού - σελ. 104, Β8. Όπως και να έχει, λόγω της συνέχειας της f - την φ εννοώ, αλλά είναι κουραστικό να γράφεις φ στο LaTeX :Ρ - το δοσμένο όριο είναι της μορφής 0/0 και μπορείς να τραβήξεις έναν de L'Hospital, μιας και το όριο που θα βρεις στο τέλος υπάρχει.

Διότι:

και

Οπότε, παίρνεις αμέσως f''(1)=3. Τώρα, αφού η δεύτερη παράγωγος είναι συνεχής και δεν έχει ρίζες, θα διατηρεί πρόσημο στο R - γνωστή συνέπεια του Θ. Bolzano - άρα, αφού f''(1)>0, έπεται ότι f''(x)>0 σε όλο το R άρα η f είναι κυρτή στο πεδίο ορισμού της.

Για το δεύτερο, έχεις το f(1)=1, σου λείπε το f'(1). Μπορείς να θεωρήσεις τη συνάρτηση:

για την οποία παρατηρείς ότι, από τη δοσμένη ανισότητα εύκολα παίρνεις:

Η g είναι παραγωγίσιμη - σύνθεση παραγωγίσιμων και διαφορές κ.λπ. - με παράγωγο:

οπότε:

Τώρα, αφού η g είναι παραγωγίσιμη, το 1 είναι στο εσωτερικό του πεδίου ορισμού της και παρουσιάζει εκεί ακρότατο από το Θ. του Fermat έχουμε g'(1)=0, άρα f'(1)=-1/3. Έτσι, η εξίσωση της εφαπτομένης είναι:

Για το τρίτο, τώρα, βοηθάει να ξαναγράψεις τη ζητούμενη εξίσωση ως εξής:

Εδώ τώρα πρέπει να κάνεις το "κλικ" και να θεωρήσεις τη συνάρτηση:

η οποία είναι παραγωγίσιμη και μάλιστα:

διότι η f είναι κυρτή, άρα και η f' γνησίως αύξουσα και χ < χ + 2. Άρα η h είναι γνησίως αύξουσα, άρα και «1-1». Παρατήρησε τώρα ότι η δοσμένη εξίσωση μπορεί να γραφτεί με τη βοήθεια της h ως εξής:

Εδώ έχεις φτάσει σε διτετράγωνη, είναι ύλη της Α' λυκείου πια. Θέτεις και στο τέλος βρίσκεις

(εκτός αν έχω κάνει λάθος τις πράξεις, πράγμα που συμβαίνει πολύ συχνά :Ρ)

 

[Papachrist]

Θα μπορούσε κάποιος να μου στείλει τις λύσεις του θέματος α4 και θέμα β αν γίνεται και σήμερα (δεν είναι μεγάλο ) για να τα μελετήσω παρακαλώ?

 

[Μάρκος Βασίλης]

Θα μπορούσε κάποιος να μου στείλει τις λύσεις του θέματος α4 και θέμα β αν γίνεται και σήμερα (δεν είναι μεγάλο ) για να τα μελετήσω παρακαλώ?
View attachment 69101

Για το Α4:
α) Λάθος γιατί λείπει η σταθερά c - π.χ. f(x)=x και g(x)=x-2.
β) Σωστό διότι υπάρχουν α,β διαφορετικά μεταξύ τους με f(α)=f(β) κ.λπ.
γ) Λάθος ενδεχομένως να ισχύει και το «=» - έχει αντιπαράδειγμα το σχολικό.
δ) Σωστό βλ. παραπάνω (ωστόσο, κακή ερώτηση για Σ-Λ)
ε) Λάθος είναι το (Β,Α).

Για το θέμα Β, επειδή έχει πάει 2 το χάραμα, ας δούμε κάποιες υποδείξεις:
Β1. Ξαναγράψε τη σχέση που σου δίνει ως εξής:

Μήπως τώρα βλέπεις αριστερά και δεξιά κάποιες παραγώγους;

Β2. Δεν έχει κάτι το ιδιαίτερο η παραγώγιση. Για την ακρίβεια, έχουμε:

και από εδώ βρίσκεις εύκολα τη δεύτερη παράγωγο και την μονοτονία - θετική παράγωγος κ.λπ.

Β3. Η f είναι γνησίως αύξουσα και στη συνέχεια λύνεις την f(x)=y ως προς x. Ίσως να πρέπει να θυμηθείς πώς λύνουμε άρρητες εξισώσεις/ανισώσεις - που, βέβαια, τα τελευταία χρόνια είναι εκτός ύλης στην Β' λυκείου. Για την ακρίβεια, έχεις:

Εδώ αφήνεις μόνο του το ριζικό, υψώνεις στο τετράγωνο και λύνεις τη δευτεροβάθμια που προκύπτει - πρόσεξε τους όποιους περιορισμούς προκύψουν.

Β4. i) Δε βλέπω τη σχέση καθαρά στο screenshot, έχει και κάτι κουτάκια, πάντως 99% παραγωγίζεις την h και βρίσκεις μηδενική παράγωγο.

ii) Εδώ είναι εύκολο. Από την απο πάνω έχεις h(x)=c και με g(0)=0 βρίσκεις το c (ή με το g'(0), δεν ξέρω τι «κρύβουν» τα κουτάκια) και μετά βρίσκεις από εκεί την g και αντικαθιστάς.

 

[kvstas92]

καλημερα φιλοι, τι εχετε να πειτε για την ραγδαια μειωση της υλης στα μαθηματικα στις πανελλαδικες?
πως τα βλεπετε τα θεματα φετος?

 

[Papachrist]

Ορίστε τα θέματα ...τώρα φαίνονται καθαρά θα ήθελα τις λύσεις για να τις μελετήσω των β3 β4 γ3 γ4

 

[Μάρκος Βασίλης]

καλημερα φιλοι, τι εχετε να πειτε για την ραγδαια μειωση της υλης στα μαθηματικα στις πανελλαδικες?
πως τα βλεπετε τα θεματα φετος?

Μια χαρά θα είναι. Δε θα πέσει DLH, αλλά, για την κυρτότητα, για παράδειγμα, και που την έκοψαν, δεν αλλάζει κάτι. Ό,τι ακριβώς λύνεται με χρήση της κυρτότητας μπορεί να λυθεί και χωρίς αυτήν - απλώς θα γίνει άμεση αναφορά στη μονοτονία της f'.

Ίσως να νταλγκαδιάσετε λίγο στο Β' θέμα που δε θα έχει ζωγραφική αλλά να θυμίσουμε ότι:

1. υπάρχει κι ο ρυθμός μεταβολής (χεχεχε),
2. είναι εντός ύλης οι γνωστές συναρτήσεις των οποίων τις γραφικές παραστάσεις γνωρίζετε και, επομένως, μαζί με μεταφορές, ανακλάσεις και τα συναφή, μπορείτε εύκολα να κληθείτε να σχεδιάσετε κάποια τέτοια γραφική παράσταση, όπως για παράδειγμα αυτήν της:

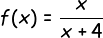
Τώρα, για πιο σύνθετα όρια, που ως τώρα είχατε μάθει να τα χειρίζεστε κυρίως με DLH, όπως, για παράδειγμα, το

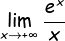
άνετα μπορεί να σας ζητηθεί να αποδείξετε μία ανισότητα σε ένα ερώτημα και μετά να υπολογίσετε το όριο με κριτήριο παρεμβολής ή θεώρημα «πραμαζώματος» κ.λπ.

Οπότε, απλώς θα γίνει μία μεγαλύτερη εστίαση στο πρώτο μέρος της ύλης και ίσως τα θέματα να γίνουν λίγο πιο τεχνικά, να εμφανιστεί κι ένα πρόβλημα μέσα στα τρία τελευταία θέματα - όπως αυτό με το σύρμα και το τετράγωνο και τον κύκλο, για παράδειγμα - ή κάτι παρεμφερές.

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 12 Απριλίου 2020

Ορίστε τα θέματα ...τώρα φαίνονται καθαρά θα ήθελα τις λύσεις για να τις μελετήσω των β3 β4 γ3 γ4
View attachment 69115View attachment 69116

Τα Β3 και Β4 πάλεψέ τα λίγο ακόμα, νομίζω ότι θα τα βγάλεις - στο Β4 δεν έχεις παρά να παραγωγίσεις την h και θα βγει.

Για το Γ3, τώρα, πρόσεξε ότι, αφού f(x)=x-1 έπεται άμεσα ότι το ζητούμενο μπορεί να ξαναγραφτεί στη μορφή:

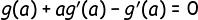
Τώρα, παρατήρησε ότι αν θεωρήσεις τη συνάρτηση s(x)=xg(x)-g(x) τότε έχεις άμεσα ότι s'(x)=g(x)+xg'(x)-g(x), και μπορείς να κάνεις ένα Rolle στην s στο [0,1], οπότε έπεται το ζητούμενο.

Για το Γ4, πρόσεξε ότι f(x)=x-1 οπότε μπορείς να γράψεις το ζητούμενο πολύ πιο απλά, αντικαθιστώντας, ως εξής - γενικά, μην κομπλάρετε σε τέτοια «τρυκ», την έχετε την f:

Τώρα, για το τελευταίο, μπορείς να κάνεις ένα Θ.Μ.Τ. στο (x,0) και να εκμεταλλευτείς την μονοτονία της g'.

 

[Μάρκος Βασίλης]

Μιας και πέρασε η ώρα, ας βάλουμε και λίγο από το Β4.

Η h είναι παραγωγίσιμη, με:

λόγω της δοσμένης σχέσης. Άρα η h είναι σταθερή και επειδή h(0)=1, έπεται ότι h(x)=1 σε όλο το R.

Για το επόμενο, ας παρατηρήσουμε ότι μπορούμε να κάνουμε το εξής:

Οπότε, έπεται ότι g(x)=x+f(x)+c, και για x=0 βρίσκεις το c=0 και όλα καλά.

 

[kvstas92]

Καλησπερα φιλοι εχετε καμια ιδεα τι κανουμε εδω? Προσπαθω τοση ωρα