*Serena*
Τιμώμενο Μέλος


Λίγη βοήθεια εδώ?Δίνεται η συνάρτηση g(x) για την οποία ισχύει:
g(x) + e^g(x) = 2x+1 για κάθε χER.
Να δείξετε ότι g(0)= 0
Να δείξετε ότι η g είναι γνησίως αύξουσα.
Να λύσετε την ανίσωση (gof)(x)> 0
Να δείξετε ότι η συνάρτηση αντιστρέφεται και να βρείτε την αντίστροφη της.

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Δίνεται η συνάρτηση g(x) για την οποία ισχύει:
g(x) + e^g(x) = 2x+1 για κάθε χER.
Να δείξετε ότι g(0)= 0
Να δείξετε ότι η g είναι γνησίως αύξουσα.
Να λύσετε την ανίσωση (gof)(x)> 0
Να δείξετε ότι η συνάρτηση αντιστρέφεται και να βρείτε την αντίστροφη της.
1. Στην (1) x=ο
άρα φ αύξουσα και "1-1"
2.
άρα g γνησίως αύξουσα.
3. Κάτι πρέπει να σου δίνει για την f
4. Ποιά συνάρτηση?
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
*Serena*
Τιμώμενο Μέλος


Είσαι θεός! Υποκλίνομαι!
1. Στην (1) x=ο
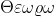
άρα φ αύξουσα και "1-1"
2.
άρα g γνησίως αύξουσα.
3. Κάτι πρέπει να σου δίνει για την f
4. Ποιά συνάρτηση?

Ξεχάστηκα... Τα έχω λύσει τα πρώτα με την f για αυτό.

f(x) = x + e^x - 1
Την g εννοούσα.


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Είσαι θεός! Υποκλίνομαι!
Ξεχάστηκα... Τα έχω λύσει τα πρώτα με την f για αυτό.
f(x) = x + e^x - 1
Την g εννοούσα.

Ωραία.
3. Φαντάζομαι έχεις βρει στα προηγούμενα ότι η f είναι αύξουσα.
4.
Στην (1) οπου x την
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος



1)δινονται οι συναρτησεις f,g με g(x)<= f(x) <= g(x)+(x-1)^2 για καθε χ ε R και g'(1)=2.N.Δ.Ο. η f ειναι παραγωγισιμη στο Χο=1 και να βρειτε την f'(1).
2)δινονται οι συναρτησεις f , g , h τετοιες ωστε f(α)=g(α)=h(α), f'(α)=g'(α) και f(x)<= g(x)<= h(x) για καθε χ ε R.Ν.Δ.Ο:
i)η συναρτηση g ειναι παραγωγισιμη στο Xo=α.
ii)g'(α)=f'(α)=h'(α).
Υ.Γ Οποιος μπορει ας εξηγησει αναλυτικα αν ειναι ευκολο.

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 278211
Επισκέπτης


καλησπερα!!!Θα ηθελα μια μεγαλη βοηθεια στις παρακατω ασκησεις γιατι πραγματικα παιδευομαι εδω και ωρες.....
1)δινονται οι συναρτησεις f,g με g(x)<= f(x) <= g(x)+(x-1)^2 για καθε χ ε R και g'(1)=2.N.Δ.Ο. η f ειναι παραγωγισιμη στο Χο=1 και να βρειτε την f'(1).
2)δινονται οι συναρτησεις f , g , h τετοιες ωστε f(α)=g(α)=h(α), f'(α)=g'(α) και f(x)<= g(x)<= h(x) για καθε χ ε R.Ν.Δ.Ο:
i)η συναρτηση g ειναι παραγωγισιμη στο Xo=α.
ii)g'(α)=f'(α)=h'(α).
Υ.Γ Οποιος μπορει ας εξηγησει αναλυτικα αν ειναι ευκολο.
1) g(x)<= f(x) <= g(x)+(x-1)²
για χ-->1 g(x)=g(1) και g(x)+(x-1)² =g(1)
Άρα σύμφωνα με το κριτήριο παρεμβολής => f(1)=g(1)
έπειτα κατασκεύασε το lim f(x)-f(1)/x-1 για χ-->1- και χ-->1+ και βρίσκεις ότι τα όρια είναι ίσα, άρα υπάρχει f'(1) και ισούται με 2.
δηλαδή: [g(x)-g(1)]/[x-1]<= f(x)-f(1)/x-1 <= [g(x)+(x-1)²-g(1)]/[x-1] για χ>1
lim [g(x)-g(1)]/[x-1]<= lim f(x)-f(1)/x-1 <= lim{[g(x)-g(1)]/[x-1] + x-1} για x-->1+
κριτήριο παρεμβολής--> lim f(x)-f(1)/x-1=g'(1)=2 για x-->1+
ομοίως: lim f(x)-f(1)/x-1=g'(1)=2 για x-->1-
επομένως: lim f(x)-f(1)/x-1 (χ-->1+)=lim f(x)-f(1)/x-1 (χ-->1-) = lim f(x)-f(1)/x-1 (χ-->1) = f'(1)=2
2)Η άσκηση αυτή είναι παρόμοια με την προηγούμενη.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
mary-blackrose
Εκκολαπτόμενο μέλος


[LATEX]g\left( x \right) =\left( \sqrt { { x }^{ 3 }+3 } -2 \right) \cdot f\left( x \right)[/LATEX]
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Rempeskes
Επιφανές μέλος


αν η συναρτηση f ειναι συνεχης στο 1, να αποδειξετε οτι η συναρτησηειναι παραγωγισιμη στο 1.Σας παρακαλω ας βοηθησει καποιος.........Code:[LATEX]g\left( x \right) =\left( \sqrt { { x }^{ 3 }+3 } -2 \right) \cdot f\left( x \right)[/LATEX]
1.
2.
3.
υγ. αη μιςς γ λυκ.
υγ2. επαληθευστε και τις πραξεις, εχω πιει λιγο.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


vimaproto
Πολύ δραστήριο μέλος


1)αν View attachment 48826 να βρειτε τα ορια
View attachment 48829καιView attachment 48827
2)αν ισχυει View attachment 48828 να βρεθει ο αεR
3)αν ισχυει View attachment 48830 να βρεθουν α και β
θα ηθελα να μου εξηγησετε πως λυνονται αυτες οι ασκησεις λιγο αναλυτικα, ευχαριστω εκ των προτερων
1) Για χ=3 ο παρονομαστής μηδενίζεται αλλά, το κλάσμα μας λέει η άσκηση παίρνει ορισμένη τιμή. Στην παράσταση που μας έδωσε θα φροντίσω να εμφανιστεί το κλάσμα που έχει συγκεκριμένο όριο (εδώ ίσο με 5). Την γράφω
(f(x)-2x+x-3)/(x²-9)=(f(x)-2x)/(x²-9)+(x-3)/(x²-9)=(f(x)-2x)/(x²-9)+1/(x+3) και το όριο είναι 5+1/6=31/6
2) Για χ=2 ο παρονομαστής μηδενίζεται αλλά, το κλάσμα μας λέει η άσκηση παίρνει ορισμένη τιμή,(=9) πρέπει και ο αριθμητής να μηδενίζεται, δηλ. να έχει έναν παράγοντα ίδιο με τον παράγοντα που μηδενίζει τον παρονομαστή.
Αντικαθιστώ στον αριθμητή χ=2 και αυτός γίνεται μηδέν. Δηλ. 16+16α+2α²-2=0 ==> α²+8α+7=0 με ρίζες α=-1 και α=-7
Για α=-1 γίνεται (2χ³ -4χ²+χ-2)/(χ-2)=(χ-2)(2χ²+1)/(χ-2)=2χ²+1 και με αντικατάσταση χ=2 δίνει 2.2²+1=9
ομοίως για την τιμή α=-7 η οποία δεν είναι αποδεκτή γιατί δεν επαληθεύει το όριο (χ-2)(2χ²-24χ+1)(χ-2)=-39
3)Ομοίως και για αυτή την άσκηση. Ο αριθμητής για χ=-2 είναι -8β+α+4=0 και α=8β-4 Τότε το κλάσμα γράφεται (βχ³+8β-4+4)/(χ+2)=
β(χ³+8)/(χ+2)=β(χ²-βχ+β²) το οποίο για χ=-2 πρέπει να ισούται με 12. Δηλ. β(4+4+4)=12 ==> β=1. Τότε α=8-4=4
Αν νυχτιάτικα έκανα κανένα λάθος να με συγχωρέσεις.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


ευχαριστω πολυ για την βοηθεια1) Για χ=3 ο παρονομαστής μηδενίζεται αλλά, το κλάσμα μας λέει η άσκηση παίρνει ορισμένη τιμή. Στην παράσταση που μας έδωσε θα φροντίσω να εμφανιστεί το κλάσμα που έχει συγκεκριμένο όριο (εδώ ίσο με 5). Την γράφω
(f(x)-2x+x-3)/(x²-9)=(f(x)-2x)/(x²-9)+(x-3)/(x²-9)=(f(x)-2x)/(x²-9)+1/(x+3) και το όριο είναι 5+1/6=31/6
2) Για χ=2 ο παρονομαστής μηδενίζεται αλλά, το κλάσμα μας λέει η άσκηση παίρνει ορισμένη τιμή,(=9) πρέπει και ο αριθμητής να μηδενίζεται, δηλ. να έχει έναν παράγοντα ίδιο με τον παράγοντα που μηδενίζει τον παρονομαστή.
Αντικαθιστώ στον αριθμητή χ=2 και αυτός γίνεται μηδέν. Δηλ. 16+16α+2α²-2=0 ==> α²+8α+7=0 με ρίζες α=-1 και α=-7
Για α=-1 γίνεται (2χ³ -4χ²+χ-2)/(χ-2)=(χ-2)(2χ²+1)/(χ-2)=2χ²+1 και με αντικατάσταση χ=2 δίνει 2.2²+1=9
ομοίως για την τιμή α=-7 η οποία δεν είναι αποδεκτή γιατί δεν επαληθεύει το όριο (χ-2)(2χ²-24χ+1)(χ-2)=-39
3)Ομοίως και για αυτή την άσκηση. Ο αριθμητής για χ=-2 είναι -8β+α+4=0 και α=8β-4 Τότε το κλάσμα γράφεται (βχ³+8β-4+4)/(χ+2)=
β(χ³+8)/(χ+2)=β(χ²-βχ+β²) το οποίο για χ=-2 πρέπει να ισούται με 12. Δηλ. β(4+4+4)=12 ==> β=1. Τότε α=8-4=4
Αν νυχτιάτικα έκανα κανένα λάθος να με συγχωρέσεις.

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


ι)να βρειτε το πεδιο ορισμου
ιι)να βριτε το οριο του f(x) οταν τινει στο 0
2)να βρειτε τα ορια
ι)
ιι)
3)Η συναρτηση f εχει συνολο τιμων το R και για καθε χε[0,+00) ισχυει:
ι)να βρειτε την f^-1
ιι) να βρειτε το οριο
παιδια α ηθελα την βοηθεια σας σε αυτες τις ασκησεις
ευχαριστω
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


πως τα βλεπετε ?1)Δινεται η συναρτηση View attachment 48842
ι)να βρειτε το πεδιο ορισμου
ιι)να βριτε το οριο του f(x) οταν τινει στο 0
2)να βρειτε τα ορια
ι)View attachment 48843
ιι)View attachment 48845
3)Η συναρτηση f εχει συνολο τιμων το R και για καθε χε[0,+00) ισχυει:View attachment 48844
ι)να βρειτε την f^-1
ιι) να βρειτε το οριο View attachment 48846
παιδια α ηθελα την βοηθεια σας σε αυτες τις ασκησεις
ευχαριστω
λυνονται ή......
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Λοιπον απο το 1ο τευχος του μπαρλα στους μιγαδικους 1ο κεφαλειο εχς απορεια τις 43, 44, 47, 49,56,57,62,67
ΘΑ ΧΑΡΩ ΠΟΛΥ ΝΑ ΜΕ ΒΟΗΘΗΣΕΙΣ
Σελίδα?32 ή 64?
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Αυτή η ρίζα βρίσκεται στον αριθμητη ενός ορίου με x --> +oo
Υγ. Βλακεία είπα. Τώρα σκέφτηκα ότι θα βγάλω το χ^4 κοινό παράγοντα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


ενταξει αυτη καταφερα να τη λυσω και την επομενη για την 3 τι λετε?Τα πεδία ορισμού είναι προφανή. Tα κλάσματαπαίρνουν την τιμή 1 όταν πλησιάζουμε στην οριακή τιμή του χ εκ δεξιών και -1 εξ αριστερών. Ετσι βρίσκουμε διαφορετικές τιμές ορίων. Αρα δεν υπάρχει όριο. Κάνε γινόμενα και χώρισε σε κλάσματα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος
antwwwnis
Διάσημο μέλος


δινεται η συναρτηση f(x)=View attachment 48872,διαφορο του 1και α, χ=1
να βρειτε αν θπαρχει το View attachment 48873
για αυτη την ασκηση τι λετε?
Τιπ: Υπολόγισε τα πλευρικά όρια. Έτσι θα έχεις τη δυνατότητα να "πετάξεις" το απόλυτο.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 9 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

