Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Ricky · 09-12-10

Αρχική Δημοσίευση από Bemanos:
να βρειτε τα ορια $\lim_{x\rightarrow + \infty}\frac{x\sin (\frac{1}{x})}{\sqrt{{x}^{2}+x}-x}$
και το $\lim_{x\rightarrow + \infty}f(x)$ εαν f(x)= $\frac{{e}^{x}+{2}^{x+1}}{{e}^{x+2}+{2}^{x}}$

ευχαριστω

Και το 2ο έχει δυσκολίες. Ιδιαίτερα στο τέλος μπορεί κανείς εύκολα να την πατήσει. Το προσπάθησες καθόλου; Αν ναι, τι ακριβώς έκανες;

Bemanos · 09-12-10

Αρχική Δημοσίευση από Ricky:
Και το 2ο έχει δυσκολίες. Ιδιαίτερα στο τέλος μπορεί κανείς εύκολα να την πατήσει. Το προσπάθησες καθόλου; Αν ναι, τι ακριβώς έκανες;

δεν βρηκα ακρη με το δευτερο εχω διαιρεσει με το e stin x και στα δυο μελη αλλα μετα... το χαος :hmm:

Ricky · 09-12-10

Αρχική Δημοσίευση από Bemanos:
δεν βρηκα ακρη με το δευτερο εχω διαιρεσει με το e stin x και στα δυο μελη αλλα μετα... το χαος

Έλα να το πάμε μαζί τότε.

Ελπίζω ότι αυτό το καταλαβαίνεις.

Έχουμε λοιπόν:

άρα

.

Εύκολα τώρα παίρνεις ότι το αρχικό όριο ισούται με

.

Chris1993 · 9 Δεκεμβρίου 2010

Αρχική Δημοσίευση από Bemanos:
δεν βρηκα ακρη με το δευτερο εχω διαιρεσει με το e stin x και στα δυο μελη αλλα μετα... το χαος

-Που το βλέπεις το χάος?

Αρχική Δημοσίευση από Ricky:
Έλα να το πάμε μαζί τότε.

Ελπίζω ότι αυτό το καταλαβαίνεις.

Έχουμε λοιπόν:

άρα

.

Εύκολα τώρα παίρνεις ότι το αρχικό όριο ισούται με

.

-Ricky , πολύ ωραία η λύση σου αλλά η άσκηση βγαίνει πολύ πιο εύκολα

Αρχική Δημοσίευση από Bemanos:
Να βρείτε το όριο : $\lim_{x\rightarrow + \infty}f(x)$ εαν f(x)= $\frac{{e}^{x}+{2}^{x+1}}{{e}^{x+2}+{2}^{x}}$

Ευχαριστώ

Ορίστε :

$f(x)=\frac{\frac{{e}^{x} + {2}^{x}\cdot 2}{{e}^{x}}}{\frac{{e}^{x}\cdot {e}^{2}+ {2}^{x}}{{e}^{x}}} = \frac{\frac{{e}^{x}}{{e}^{x}}+\frac{{2}^{x}\cdot 2}{{e}^{x}}}{\frac{{e}^{x}\cdot {e}^{2}}{{e}^{x}} + \frac{{2}^{x}}{{e}^{x}}} = \frac{1 + ({\frac{2}{e})}^{x}\cdot 2}{{e}^{2}+{(\frac{2}{e})}^{x} }$
Άρα,
$\lim_{+\propto }f(x) = \lim_{+\propto } \frac{1 + ({\frac{2}{e})}^{x}\cdot 2}{{e}^{2}+{(\frac{2}{e})}^{x} } = \frac{1+0\cdot 2}{{e}^{2} + 0} = \frac{1}{{e}^{2}}$

Φιλικά,
Χρήστος

Bemanos · 09-12-10

Αρχική Δημοσίευση από Chris1993:
-Που το βλέπεις το χάος?

-Ricky , πολύ ωραία η λύση σου αλλά η άσκηση βγαίνει πολύ πιο εύκολα

Ορίστε :

$f(x)=\frac{\frac{{e}^{x} + {2}^{x}\cdot 2}{{e}^{x}}}{\frac{{e}^{x}\cdot {e}^{2}+ {2}^{x}}{{e}^{x}}} = \frac{\frac{{e}^{x}}{{e}^{x}}+\frac{{2}^{x}\cdot 2}{{e}^{x}}}{\frac{{e}^{x}\cdot {e}^{2}}{{e}^{x}} + \frac{{2}^{x}}{{e}^{x}}} = \frac{1 + ({\frac{2}{e})}^{x}\cdot 2}{{e}^{2}+{(\frac{2}{e})}^{x} }$
Άρα,
$\lim_{+\propto }f(x) = \lim_{+\propto } \frac{1 + ({\frac{2}{e})}^{x}\cdot 2}{{e}^{2}+{(\frac{2}{e})}^{x} } = \frac{1+0\cdot 2}{{e}^{2} + 0} = \frac{1}{{e}^{2}}$

Φιλικά,
Χρήστος

Αρχική Δημοσίευση από Ricky:
Έλα να το πάμε μαζί τότε.

Ελπίζω ότι αυτό το καταλαβαίνεις.

Έχουμε λοιπόν:

άρα

.

Εύκολα τώρα παίρνεις ότι το αρχικό όριο ισούται με

.

thanks

Chris1993 · 09-12-10

Έχεις λοιπόν 2 τρόπους

Τίποτα

Ricky · 09-12-10

Αρχική Δημοσίευση από Chris1993:
-Ricky , πολύ ωραία η λύση σου αλλά η άσκηση βγαίνει πολύ πιο εύκολα
Φιλικά,
Χρήστος

Μπράβο Χρήστο! Περίμενα ότι ίσως χρειαστεί Hospital κάπου για αυτό και τα έφερα σε αυτή τη μορφή.

Chris1993 · 09-12-10

Ευχαριστώ πολύ

Εμείς δεν έχουμε φτάσει De L'Hopital ακόμα πάντως

Μια χαρά...πολύ ωραία η λύση σου αλλά λίγο δύσκολη να την σκεφτεί ένας μαθητής

ilias77 · 09-12-10

Καλησπέρα μια μικρη βοήθεια σε μια ασκηση.

έστω οι συνεχεις συναρτησεις f:{a,b}--->R με f(a)=g(b) και f(b)=g(a) ν.δ.ο η Cf kai Cg τέμνονται σε ένα τοθλαχιστον σημειο με τετμημένη X ε{a,b}

{ } αυτο ειναι το κλειστό διάστημα.

Ricky · 09-12-10

Αρχική Δημοσίευση από ilias77:
Καλησπέρα μια μικρη βοήθεια σε μια ασκηση.

έστω οι συνεχεις συναρτησεις f:{a,b}--->R με f(a)=g(b) και f(b)=g(a) ν.δ.ο η Cf kai Cg τέμνονται σε ένα τοθλαχιστον σημειο με τετμημένη X ε{a,b}

{ } αυτο ειναι το κλειστό διάστημα.

Πάρε τη συνάρτηση h: [a,b]->R με h(x)=f(x)-g(x).

Προσπάθησε να δείξεις ότι h(a)*h(b)<0 και μετά εφάρμοσε το θεώρημα Bolzano.

ilias77 · 09-12-10

δηλαδα θα πρεπει να δειξω οτι ειναι γνησιως φθίνουσα?

Ricky · 09-12-10

Αρχική Δημοσίευση από ilias77:
δηλαδα θα πρεπει να δειξω οτι ειναι γνησιως φθίνουσα?

Όχι. Πρώτα από όλα διάβασε τι λέει το θεώρημα Bolzano. :/:

ilias77 · 09-12-10

το εχω διαβασει....και η αποδειξη πρπεει να βοηθαει.....δεν θα πρεπει να πρωτα να δειξουμε οτι η συναρτηση ειναι γνησιως μονοτονη?

koum · 09-12-10

Αρχική Δημοσίευση από ilias77:
το εχω διαβασει....και η αποδειξη πρπεει να βοηθαει.....δεν θα πρεπει να πρωτα να δειξουμε οτι η συναρτηση ειναι γνησιως μονοτονη?

Ο Ricky σου πρόδωσε την λύση 2 post πιο πάνω.
Θεώρησε τη συνάρτηση $h(x)=f(x)-g(x)$ και βρες το πρόσημο του γινομένου
$h(a)\cdot h(b)=(f(a)-g(a))(f(b)-g(b))$ . Μετά μπαίνει στον αυτόματο πιλότο... :thumbup:

Ricky · 9 Δεκεμβρίου 2010

Αρχική Δημοσίευση από ilias77:
το εχω διαβασει....και η αποδειξη πρπεει να βοηθαει.....δεν θα πρεπει να πρωτα να δειξουμε οτι η συναρτηση ειναι γνησιως μονοτονη?

Λέει πουθενά η εκφώνηση του θεωρήματος Bolzano ότι η συνάρτηση πρέπει να είναι μονότονη;

vavlas · 09-12-10

Αρχική Δημοσίευση από ilias77:
Καλησπέρα μια μικρη βοήθεια σε μια ασκηση.

έστω οι συνεχεις συναρτησεις f:{a,b}--->R με f(a)=g(b) και f(b)=g(a) ν.δ.ο η Cf kai Cg τέμνονται σε ένα τοθλαχιστον σημειο με τετμημένη X ε{a,b}

{ } αυτο ειναι το κλειστό διάστημα.

Από το μπάρλα είναι;
Πρέπει να την έχω κάνει.
Αν κάνεις αυτά που σου είπαν πιο πάνω καταλήγεις σε h(a)h(b)=-(f(a)-f(b))² και μετά μπλα μπλα.

ilias77 · 10-12-10

οκ ευχαριστω παιδια......το εψαχα λιγο το θεματακι και καταλαβα τι γινετε και παλι 1000 ευχαριστω

skiouroosasdf · 10-12-10

Αρχική Δημοσίευση από styt_geia:
Αν $\xi<1$

επειδή $f(1)=1>0=f(\xi)$ , η f είναι γνησίως αύξουσα, άρα $x>\xi\Rightarrow f(x)>f(\xi)=0\Rightarrow f(x)(1-\xi)>0$

Αν $\xi>1$

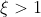
επειδή $f(1)=1>0=f(\xi)$ , η f είναι γνησίως φθίνουσα, άρα $x>\xi\Rightarrow f(x)<f(\xi)=0\Rightarrow f(x)(1-\xi)>0$

κατάλαβα ευχαριστώ!!

tsoump · 14-12-10

Καλησπέρα . Έχω κι εγώ δυο απορίες στο Θ.Μ.Τ.

Βιβλίο: Μπάρλας 2ο τεύχος

Ας θέσω την πρώτη.

σελ 62 , ασκ 28

Έστω μια συνάρτηση f που είναι δυο φορές παραγωγίσιμη στο R. Αν η εφαπτομένη στη Cf στο Α ( α , f(α) ) τέμνει τη Cf στο B ( β , f(β) ), β>α , να δείξετε ότι:
i) Η f ' δεν είναι 1-1
ii) Υπάρχει ξ ανήκει στο ( α , β ) τέτοιο , ώστε f " ( ξ ) = 0

Η Σκέψη μου .

Να προσπαθήσω να το αποδείξω με άτοπο .
Για να είναι μια συνάρτηση 1-1 θα πρέπει (απο μονοτονία) στο ( α , β ) μα ισχύει f(α) < f(β) .

Leo 93 · 15-12-10

Το ότι μια συνάρτηση είναι 1-1 δε σημαίνει ότι είναι και γν. μονότονη. Δες το γραφικά.
Εκτός αν εννοείς ότι επειδή f' 1-1 και συνεχής είναι γν. μονότονη, αλλά δεν θα χρειαστεί.

ι) Το (α,f(α)) επαληθεύει την εξίσωση της εφ. στο Α και τελικά f'(α) = [f(β) - f(α)] / (β - α)
Θ.Μ.Τ. στο [α,β]: υπάρχει ξ στο (α,β): f'(ξ) = [f(β) - f(α)] / (β - α)

ιι) Rolle στο [α,ξ]

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Περιβόητο μέλος

Πολύ δραστήριο μέλος

Περιβόητο μέλος

Εκκολαπτόμενο μέλος

Περιβόητο μέλος

Νεοφερμένο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένο μέλος

Νεοφερμένο μέλος

Νεοφερμένο μέλος

Εκκολαπτόμενο μέλος