Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[Dias]

Να βρεθουν οι μιγαδικοι αριθμοι z για τους οποιους ο z² ειναι αρνητικος πραγματικος αριθμος

Βάλε z = x + yi, ύψωσε στο τετράγωνο, βάλε πραγματικό μέρος <0, φανταστικό = 0.
Λύση
z² = (χ+yi)² = χ² + 2xyi + y²i² = χ² - y² + 2xyi
Θέλουμε 2χy = 0 και χ² - y² <0
Από την 1η χ=0 ή y=0. Για y=0 η 2η δεν γίνεται, ενώ για χ=0 η 2η ισχύει για y≠ 0.
Άρα z = yi με y∈R*

​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[red span]

παιδια μπορειτε να παρουσιασετε την λυση παρακαλω

Βάλε z = x + yi, ύψωσε στο τετράγωνο, βάλε πραγματικό μέρος <0, φανταστικό = 0.
Βγαίνει z = yi με y∈R* (y≠0)

​

δηλαδη z²=χ²+2χyi-y²
χ²-y²<0 και 2χy=0 x=0 και y=0
για χ=0 yδιαφορο0 δηλαδη y>0 z=yi για y=0 x²<0 ατοπο
καπως ετσι? ναι

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[red span]

Ειναι μια ασκηση που λεει
z²-(z)=2
ν.δ.ο
(z²)=2+(z)
ξερω οτι πρεπει να το πας απο το αλλο μερος και να βαλεις μετρα δηλ
(z²)=(2+(z))
και καταληγω εδω δεν ξερο πως να απαληψω το μετρο στο 2 μελος ωστε να το φερω στην μορφη που θελω να αποδειξω.
σκεφτηκα την τριγωνικη αλλα δεν ξερω
παρακαλω βοηθεια
Υ.Γ οπου ( εννοω μετρα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dias]

....και καταληγω εδω δεν ξερω πως να απαλειψω το μετρο στο 2 μελος .....

Το 2+|z| δεν είναι πραγματικός θετικός? Και το |2+|z|| απόλυτη τιμή? Άρα....
Υ.Γ. |z|: το πλήκτρο πάνω από το δεξί Shift σου δίνει το | (με Shift).

​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[ProfessoR]

πως λύνεται η εξίσωση x*2=2*x

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dias]

πως λύνεται η εξίσωση x*2=2*x

Τα αστεράκια εννοείς εκθέτες? Δηλαδή: χ² = 2ˣ ?
Αν εννοείς αυτό: προφανής λύση χ=2.

​

Υ.Γ. Δεν βλέπω πώς μπορεί να βγει. Η λογαρίθμιση δεν δίνει κάτι. Αν δεν βρεις κάτι άλλο γράψτο κατευθείαν. Αν βρεις ή σου δείξουν, πες το μου να μου λυθεί κι εμένα η απορία.
.
​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[ProfessoR]

ναι αλλά πως θα το γράψω είναι το πρόβλημα να το γράψω κατευθείαν?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dias]

Υπάρχει και δεύτερη λύση: χ ≃ - 3/4
για την ακριβεια: χ = -0,7666646959621

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dias]

Και υπάρχει και 3η λύση χ=4.
Άρα 3 λύσεις: χ = 2 , χ = 4 , χ = -0,7666646959621
.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dias]

Τελικά μάλλον η άσκηση δεν λύνεται με γνώσεις λυκείου. Έψαξα στο ίντερνετ. (Κάντε αν θέλετε και εσείς αναζήτηση: "χ^2=2^χ" ). Βρήκα αυτά:
https://mathforum.org/library/drmath/view/54607.html
https://www.newton.dep.anl.gov/askasci/math99/math99274.htm
https://forums.xkcd.com/viewtopic.php?f=17&t=5918
Σε μαθηματικά φόρουμ του εξωτερικού συζητάνε για λύση της εξίσωσης χ² = 2ˣ και καταλήγουν ότι δεν γίνεται παρά μόνο με την μέθοδο Newton-Raphson (δεν την ξέρω την κυρία) ή και άλλες μεθόδους (εντελώς σκοτεινές για μένα). Από όσο μπόρεσα να καταλάβω με τη μέθοδο αυτή Νewton-Raphson βρίσκουμε ρίζες σε μια εξίσωση προσεγγιστικά. Βάζουμε στην τύχη κάποιον αριθμό για ρίζα και χρησιμοποιώντας παραγώγους και κάποιον τύπο, βρίσκουμε άλλο αριθμό που τον ξαναβάζουμε και όλο και πλησιάζουμε τη ρίζα με όσο δυνατόν μεγαλύτερη προσέγγιση. Δεν κατάλαβα πώς βρίσκουμε τις περισσότερες ρίζες, αλλά δεν νομίζω ότι μπορώ ακόμα να το καταλάβω. Το σίγουρο είναι ότι η μέθοδος αυτή δεν είναι ύλη λυκείου. Πάντως βρίσκουν τις ίδιες λύσεις που βρήκα με τη γραφική παράσταση. Θα περιμένω να μας πει ο φίλος που του έδωσαν την άσκηση, πώς του την έλυσαν. Αν αυτοί ή κάποιος άλλος βρήκε λύση με ύλη λυκείου, να την πούμε στους ξένους μαθηματικούς να τους βάλουμε τα γυαλιά.

​

Λάουρα: Μην κάνεις merge σ΄αυτό το μήνυμα. Κάνε στα δύο προηγούμενα. ​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Boom]

Με παραγώγους δοκιμάσατε;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[akiroskirios]

και είπα να το γράψω χθες πως δν λύνεται με γνώσεις λυκείου αλλά φοβήθηκα μην εκτεθώ

ΥΓ: θεοδώρα αν εννοείς να θέσω συνάρτηση και να τη μελετήσω ώστε κάπως έτσι να βρω τις λύσεις (ή έστω να αποδείξω με μονοτονία πως δν υπάρχουν άλλες), ναι το δοκίμασα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Boom]

Τότε όμως γιατί βρίσκεται στο θέμα των μαθηματικών κατεύθυνσης γ' λυκείου;
Η αλήθεια είναι πως και εμένα δε μου λέει κάτι αλλά τα έχω ξαχάσει κιόλας.
Πάντως τα σχετικά θεωρήματα, ΘΜΤ και λοιπά, νομίζω απορρίπτονται γιατί εκείνα λένε απλά ότι υπάρχει ρίζα, χμ ενδιαφέρον φαίνεται

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[akiroskirios]

Τότε όμως γιατί βρίσκεται στο θέμα των μαθηματικών κατεύθυνσης γ' λυκείου;

για να μην τα ξεχάσω σαν κι εσένα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dias]

Ο φίλος που έβαλε την άσκηση είναι νέο μέλος στο φόρουμ και από ότι φαίνεται από τα στοιχεία που δίνει θα παει τώρα Γ λυκείου. Είχε δημουργήσει νέο θέμα, αλλά μεταφέρθηκε σ΄αυτό. Από όσα γράφει προκύπτει ότι μάλλον κάποιος του έβαλε την άσκηση. Δεν μας είπε όμως πάνω σε ποια ύλη δουλεύει. Το πιο πιθανό είναι να βρίσκεται στα πρώτα των συναρτήσεων ή να κάνει επανάληψη των εκθετικών της Β λυκείου. Το έψαξα κι εγώ για ΘΜΤ μονοτονίες κλπ πριν κάνω αναζήτηση με τον Γκούγκλη. Πάντως, φαντάζομαι ότι αν γινόταν αλλιώς οι ξένοι μαθηματικοί δεν θα έλεγαν όσα βρήκα. Άρα ας καταλήξουμε ότι δεν γίνεται με ύλη λυκείου. Καλό όμως θα ήταν να μας πει μερικά πράγματα ο φίλος που έβαλε την άσκηση. Ομολογώ ότι μου έχει κινηθεί το ενδιαφέρον.

​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[akiroskirios]

μπορεί να τον προκάλεσαι κανένας φίλος του να λύσει μία (τόσο απλή) εξίσωση...

ΥΓ: Δία, σε βλέπω μπενοβγαίνεις...πώς την έχεις δει? μία άσκηση λύνεις, ένα μήνυμα ποστάρεις?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dias]

Δία, σε βλέπω μπαινοβγαίνεις...πώς την έχεις δει? μία άσκηση λύνεις, ένα μήνυμα ποστάρεις?

Γιες, δατς ιτ!!! Σε κάθε άσκηση που λύνω (εμβαδά με ορισμένο ολοκλήρωμα) κάνω γκιφτ στον μαησέλφ μου ένα λογκίνι στο Αη-σκούληκι!!

​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[exc]

Πριν διαβάσετε αυτό το μήνυμα, οφείλω να σας πω ότι πρόκειται για κακή καταγραφή των σκέψεών μου, αλλά δεν μπορούσα να τα εκφράσω, αυτή τη στιγμή τουλάχιστον, καλύτερα.
Αν αντέχετε, διαβάστε το μήνυμα... Ελπίζω να καταλάβετε τι εννοώ...

Για την εξίσωση x^2=2^x.

Spoiler

Παιδιά, με γνώσεις Γ' λυκείου λύνεται η εξίσωση.
Απλώς τελικά δεν μπορείτε να βρείτε αριθμούς, γιατί δεν είστε υπολογιστές και δεν μπορεί να λυθεί πλήρως αλγεβρικά.

Βρίσκουμε τις πρώτες 3 παραγώγους της συνάρτησης x^2-2^x.
Από αυτές βρίσκουμε ότι η 3η παράγωγος είναι αρνητική και άρα η 2η είναι γνησίως φθίνουσα, οπότε αν έχει μία ρίζα είναι η μοναδική.
Η 2η λύνεται αλγεβρικά. Αριστερά από τη ρίζα (=ρ) είναι θετική και δεξιά αρνητική, άρα η 1η είναι αριστερά από αυτήν γνησίως αύξουσα και δεξιά γνησίως φθίνουσα και εκεί παρουσιάζει μέγιστο έναν θετικό αριθμό που δε μας βολεύει φυσικά γιατί έχει ρίζες και όμως δε λύνεται αλγεβρικά (εγώ τουλάχιστον δε μπορώ να τη λύσω...). Το ότι όμως σε αυτό το μέγιστο-ακρόατο δεν μηδενίζεται σημαίνει ότι στους μηδενισμούς της τέμνει τον άξονα χ και δεν εφάπτεται με αυτόν. Άρα αλλάζει πρόσημο.
Μπορεί λοιπόν να μην λύνεται αλγεβρικά, λύνεται, όμως, με Bolzano. Ο υπολογιστής μπορεί να πάρει όσο μικρά διαστήματα θέλετε και να σας πει σε ποια αλλάζει το πρόσημο της συνάρτησης. Το μόνο που χρειάζεται να ξέρετε είναι λίγο προγραμματισμό (C, Fortran και ειδικά η δεύτερη είναι ιδανικές). Βρίσκεται λοιπόν τις ρίζες της πρώτης παραγώγου.*** (βλ. 2ο spoiler)
Η παράγωγος έχει το πολύ δύο ρίζες όπως είπαμε πριν. Μία αριστερά από την ρ και μία δεξιά. Θα βρείτε όντως δύο ρίζες αν κάνετε αυτό που σας λέω, άρα αυτές είναι και οι μοναδικές. Έστω ότι αυτές είναι οι ρ1, ρ2 με ρ1<ρ2.
Τότε ελέγχετε μήπως μηδενίζεται η αρχική συνάρτηση σε αυτές. Θα δείτε ότι εδώ δε μηδενίζεται. Θα βρείτε ότι για χ<ρ1 η συνάρτηση είναι γν. φθίνουσα, για ρ1<χ<ρ2 γν. αύξουσα και για χ>ρ2 γν φθίνουσα. Υπάρχουν δύο προφανείς ρίζες της συνάρτησης, οι 2 και 4. Η 4 ανήκει στο τρίτο διάστημα και είναι η μοναδική λύση σε αυτό. Η 2 στο δεύτερο διάστημα και είναι η μοναδική λύση σε αυτό και λείπει μία που μόνο με Bolzano και με πρόγραμμα μπορούμε να λύσουμε.
Μπορεί να μη μπορεί να λυθεί μόνο με στυλό και χαρτί (όχι τουλάχιστον στην εποχή που ζούμε), αλλά το μόνο που χρειάζεται από μαθηματικά είναι γνώσεις Γ' λυκείου.

*** Η παραπομπή:

Spoiler

Αν κάποιος ζητούσε ΜΟΝΟ τις ΘΕΤΙΚΕΣ ρίζες, μπορούσε να λυθεί κανονικά χωρίς υπολογιστή:
Κάνουμε ό,τι είπα παραπάνω μέχρι και τη μελέτη της 1ης παραγώγου.
Κάνουμε γραφική παράσταση με το χέρι μας και χωρίς καμία απαιτούμενη ακρίβεια (ένα πρόχειρο σχήμα - ποιοτικής "περιγραφής") των συναρτήσεων 2χ και (ln2)*2^x (υπενθυμίζω ότι η 1η παργάγωγος ισούται με 2χ-(ln2)*2^x). Βλέπουμε πρόχειρα από αυτό ότι τα σημεία τομής αυτών των καμπύλων είναι δύο στα θετικά χ, άρα και η πρώτη παράγωγος έχει δύο μηδενισμούς στα θετικά χ. Από τη μονοτονία της βλέπουμε ότι πριν τον πρώτο μηδενισμό της είναι αρνητική. Η αρχική συνάρτηση στο 0 είναι επίσης αρνητική και συνεχίζει να μειώνεται μέχρι τον 1ο μηδενισμό της 1ης παραγώγου. Άρα ο τρίτος μηδενισμός (που υπάρχει από τη μονοτονία της συνάτησης) της αρχικής συνάρτησης είναι σίγουρα στα αρνητικά χ αφού ισχύουν και τα παρακάτω...
Είπα από πριν ότι η 1η παράγωγος παρουσιάζει θετικό μέγιστο στο ρ που περίπου ίσο με 2.057 (και βρίσκεται αλγεβρικά). Εμείς έχουμε δύο προφανείς ρίζες της αρχικής συνάρτησης την 2 και την 4. Βάζοντας το 4>ρ στην πρώτη παρ. βλέπουμε ότι είναι αρνητική, άρα είμαστε στο διάστημα πέραν από τον μηδενισμό της (1ης παρ) και εκεί είναι μοναδική (για την αρχική). Βάζοντας την 2<ρ Βλέπουμε ότι είναι θετική άρα βρισκόμαστε στο διάστημα μεταξύ των μηδενισμών της και εκεί είναι μοναδική. Άρα βρήκαμε τις δύο μοναδικές θετικές λύσεις.

Εικόνα με την συνάρτηση και τις τρεις πρώτες παραγώγους της:

Spoiler

ΥΓ: free πρόγραμμα για 2D γραφικές παραστάσεις: https://www.padowan.dk/graph/

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dias]

@ exc
-- Νομίζω ότι κατάλαβα, όμως έχω τις αντιρρήσεις μου.
Λες ότι: "Παιδιά, με γνώσεις Γ' λυκείου λύνεται η εξίσωση".
Θα μου επιτρέψεις να πω ότι αυτό το θεωρώ πολύ θεωρητικό και τραβηγμένο διότι:
1) Μόνος σου το λες ότι: "Απλώς τελικά δεν μπορείτε να βρείτε αριθμούς, γιατί δεν είστε υπολογιστές ". Θα θυμάσαι κι εσύ ότι όταν ήσουν υποψήφιος, ότι σαν "εντός" θεωρούσες μια άσκηση που θα μπορούσες να τη λύσεις στις εξετάσεις χωρίς calculator και μόνον με το στυλό σου. Προφανώς, πράξεις της μορφής ρ = 1 - {[2ln(ln2)]/ln2} = 2,057 δεν θα μπορούσαν να ζητηθούν στις εξετάσεις.
2) Δεν νομίζω ότι είναι πρακτικά γνώση Γ λυκείου μια εξίσωση που όπως γράφεις "δεν μπορεί να λυθεί πλήρως αλγεβρικά". Αν δεν σε εκτιμούσα ότι είσαι σωστό άτομο, θα έλεγα ότι αστιεύεσαι όταν λες ότι: "Ο υπολογιστής μπορεί να πάρει όσο μικρά διαστήματα θέλετε και να σας πει σε ποια αλλάζει το πρόσημο της συνάρτησης. Το μόνο που χρειάζεται να ξέρετε είναι λίγο προγραμματισμό (C, Fortran και ειδικά η δεύτερη είναι ιδανικές)", αφού ξέρεις πολύ καλά ότι ούτε προγραμματισμό γνωρίζουμε ούτε θα πάμε στις εξετάσεις με το laptop μας.
3) Ακόμα και για την περίπτωση που θέλαμε μόνον τις θετικές ρίζες, γράφεις ότι "υπάρχουν δύο προφανείς ρίζες της συνάρτησης, οι 2 και 4". Αυτό δεν νομίζω ότι είναι δεκτό στις πανελλήνιες. Ίσως να μην έχω ακόμα μπει στα βαθειά (καθώς έχω βγάλει την ύλη μόνον πρώτο χέρι και χρειάζομαι πολλή δουλειά ακόμα), αλλά δεν έχω συναντήσει άσκηση που να βγάζουμε με το μάτι προφανείς κάποιες ρίζες και ύστερα με Bolzano να αποδεικνύουμε ότι είναι οι μοναδικές. (Ίσως αν η εκφώνηση έδινε τις προφανείς λύσεις και ζητούσε να αποδείξουμε ότι δεν υπάρχουν άλλες, θα έστεκε η άσκηση).
-- Θέλω να καταλήξω ότι μπορεί θεωρητικά η άσκηση να είναι γενικά στις γνώσεις της Γ λυκείου, αλλά δεν θα μπορούσε να είναι θέμα εξετάσεων. Φυσικά, μπορεί να κάνω λάθος σε όσα γράφω, καθώς δεν έχω την εμπειρία του εντελώς προετοιμασμένου υποψήφιου και εδώ δέχομαι ευχαρίστως να με διορθώσεις. Πάντως σε ευχαριστώ πολύ για το ενδιαφέρον και τον κόπο σου. Πιστεύω ότι ο όλος προβληματισμός που έβαλες με ωφέλησε καθώς με έκανε να σκεφτώ για να καταλάβω ορισμένα πράγματα. Εκείνο που δεν πολυκατάλαβα είναι ο πρόλογος που έβαλες, αν θέλεις εξηγείς λίγο καλύτερα τι θέλεις να πεις.

​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Λεωνίδας_Δ]

Εγώ πάντως δε το έλυνα έτσι...
Αλλά έτσι:


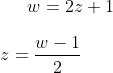
άρα η ισότητα των μέτρων που μας έδωσες γίνεται:

Και γω έτσι έλυνα παρόμοιες ασκήσεις.Προσπαθείς να φτιάξεις στην ουσία το ζητούμενο(δεν ξέρω πώς μπαινουν τα μέτρα στν υπολογιστή).Αν έχεις Μπάρλα θα δείς και στις λυμένες ασκήσεις τον ίδιο τρόπο,στις πρώτες σελίδες(στα μέτρα μιγαδικών).

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.