Βοήθεια/Απορίες στην Άλγεβρα

djimmakos · 07-02-09

Το πινακάκι φτιάχνεται βρίσκοντας τις ρίζες του τριώνυμου και λέγοντας:

Όταν Δ>0:

Για κάθε τιμή του χ που βρίσκεται μέσα στο διάστημα που ορίζεται από τις ρίζες το πρόσημο του τριωνύμου είναι ετερόσημο του α και έξω απ' αυτό το διάστημα
ομόσημο..
(Οι ρίζες της εξίσωσης προφανώς δεν συμπεριλαμβάνονται, έτσι δεν είναι; Μιλάμε για ανοιχτά διαστήματα; )

Όταν Δ=0:

Είναι παντού ομόσημο του α εκτός από το σημείο Χο, δλδ τη διπλή ρίζα της εξίσωσης, διότι εκεί μηδενίζεται (ΠΡΟΣΟΧΗ: Δε μιλάμε για αρνητικό πρόσημο στο Χο, αφού εκεί μηδενίζεται το τριώνυμο)

Όταν Δ<0:

Είναι παντού ομόσημο του α

Οκ μέχρι εδώ, αλλά στο σ' αυτό που έγραψε ο στέλιος, κάνοντας τις πράξεις, λείπει ο πρωτοβάθμιος όρος, άρα δε χρειάζεται να βρούμε τις ρίζες..Έτσι δεν είναι; :what:

mostel · 07-02-09

Έστω ότι δεν το έχουν κάνει . Τότε, πάλι έιναι απλό. Μια παράσταση είναι μεγαλύτερη ή ίση του 0 , όταν και μόνο όταν οι δύο παρενθέσεις ή είναι και οι δύο ταυτοχρόνως θετικές ή και οι δύο ταυτοχρόνες αρνητικές. Δηλαδή ότι ισχύει:

Ή:

$x+\sqrt{5}\geq 0\quad\&\quad x-\sqrt{5}\geq 0$ (κρατάμε κοινές λύσεις)

ή

$x+\sqrt{5}\leq 0\quad\&\quad x-\sqrt{5}\leq 0$ (κρατάμε πάλι κοινές λύσεις)

Συνολικώς, το πεδίο ορισμού της συνάρτησης είναι η ένωση των κοινών αυτών λύσεων που ισχύουν στην πρώτη και δεύτερη περίπτωση αντιστοίχως.

Στέλιος

makedonikosole · 11 Ιουλίου 2012

${x}^{2\geq }5\Leftrightarrow \sqrt{{x}^{2}}\geq \sqrt{5}\Leftrightarrow \left|x \right|\geq \sqrt{5}\Leftrightarrow x\succeq \sqrt{5}ήx\leq -\sqrt{5}$
-----------------------------------------
στελιο η λυση σου ειναι σωστη αλλα δεν ενδεικνυται οταν η μορφη του τριωνυμου ειναι ελλιπης δηλαδη οταν β=0 οταν δεν ειναι ελλιπης η μορφη του τριωνυμου θα το λυνεται οπως ειπε ο στελιος δηλαδη με πινακακι και προσημο τριωνυμου που θα τα μάθετε στο τέλος της πρώτης λυκείου

να ρητοποιήσετε το κλάσμα Α= $\frac{{x}^{2}}{\sqrt[3]{{x}^{2}}}$

Shadowfax · 07-02-09

Πολλαπλασίασε αριθμητή και παρανομαστή με το $\sqrt[3]{x}$

Edit: Α, άσκηση ήταν. Ε βάλτο κι εσύ στο ανάλογο θέμα να ξέρουμε τι συμβαίνει.

mostel · 11 Ιουλίου 2012

Αρχική Δημοσίευση από makedonikosole:
${x}^{2geq }5Leftrightarrow sqrt{{x}^{2}}geq sqrt{5}Leftrightarrow left|x right|geq sqrt{5}Leftrightarrow xsucceq sqrt{5}ήxleq -sqrt{5}$
-----------------------------------------
στελιο η λυση σου ειναι σωστη αλλα δεν ενδεικνυται οταν η μορφη του τριωνυμου ειναι ελλιπης δηλαδη οταν β=0 οταν δεν ειναι ελλιπης η μορφη του τριωνυμου θα το λυνεται οπως ειπε ο στελιος δηλαδη με πινακακι και προσημο τριωνυμου που θα τα μάθετε στο τέλος της πρώτης λυκείου

It's just another way...

Στέλιος

$\sqrt[3]{x^2}=u$ , κ.λπ.

Chris1993 · 07-02-09

${x}^{2} \geq {5} <=> \sqrt{{x}^{2}} \geq \sqrt{5} <=> |x| \geq \sqrt{5}$

'Αρα :

$x \geq \sqrt{5}$ και $- x \geq \sqrt{5} <=> x \leq -\sqrt{5}$

So...

$x\in R ( - \propto , -\sqrt{5} ] \upsilon [ \sqrt{5} , + \propto )$

djimmakos · 07-02-09

Αρχική Δημοσίευση από mostel:
Θέμα προετοιμασίας για όσους δώσουν μαθηματική εταιρία...

Άσκηση by me:

Αν $a,b,c>0$ και ισχύει:

$a+b+c=3$ ,

Να δειχθεί ότι:

$frac{1}{a}+frac{1}{b}+frac{1}{c}geq 3$

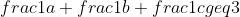
Τώρα που το θυμήθηκα ας κεράσω και εγώ μια λύση:p

Ισχύει ότι:

Αν $a,b,c>0$ και x,y,z τυχαίοι πραγματικοί αριθμοί τότε:

$\frac{x^2}{a}+\frac{y^2}{b}+\frac{z^2}{c}\geq \frac{(x+y+z)^2}{a+b+c}$ (Την απόδειξη την αφήνω σαν άσκηση

) (ΙΔΙΟΤΗΤΑ 1)

Τώρα πίσω στην ανισότητα που έδωσε ο Στέλιος.

Θέλουμε να δείξουμε ότι:

Αν $a+b+c=3$ με $a,b,c>0$ τότε ισχύει: $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\geq 3$

ΑΠΟΔΕΙΞΗ

$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1^2}{a}+\frac{1^2}{b}+\frac{1^2}{c}$

και σύμφωνα με την ιδιότητα 1 που έγραψα έχουμε:

$\frac{1^2}{a}+\frac{1^2}{b}+\frac{1^2}{c}\geq \frac{(1+1+1)^2}{a+b+c}=\frac{9}{3}=3$

και η απόδειξη ολοκληρώθηκε....

ΤΟΣΟ ΑΠΛΑ!!

Κάνω παράθεση και το μήνυμά μου όταν πρωτοείδα την άσκηση για να θυμάμαι ότι έχω αλλάξει:p (Το ψώνιο θα λέτε:p)

Αρχική Δημοσίευση από Djimmakos:
Τις ταυτότητες τις ξέρω....

Τώρα για να την έλυνα...μπα

βιλλαρασ · 14-02-09

3x^2+2(α+β+γ)χ+(αβ+βγ+γα)=0

και λεει να αποδειξω οτι εχει διπλη λυση ΑΝ ΚΑΙ ΜΟΝΟ ΑΝ α=β=γ

εγω σκεφτηκα πως αφου Δ=0 τοτε

χ=-(α+β+γ)/α αρα η μονη περιπτωση να εχει μοναδικη λυση ειναι να ειναι ισα α=β=γ ωστε ο αριθμητης να παραμενει σταθερος! και η λυση να ειναι
χ=-α=-β=-γ

djimmakos · 14-02-09

Καταρχήν είσαι σίγουρος ότι είναι έτσι η εξίσωση;...Στο σταθερό έχεις βα και αβ, το οποίο είναι το ίδιο πράγμα.. Νομίζω πρέπει να είναι (αβ+βγ+γα)...

'Εχω την εντύπωση ότι ο συλλογισμός σου είναι λάθος...Καλύτερα να δουλέψεις με τη Διακρίνουσα...

Επιπλέον λες ότι για να έχει ΜΟΝΑΔΙΚΗ ΛΥΣΗ πρεπει α=β=γ...

Εμείς θέλουμε να αποδείξουμε ότι έχει ΔΙΠΛΗ ΛΥΣΗ αν και μονο αν α=β=γ

(ΛΥΣΗ) (ΜΕ ΤΗΝ ΠΡΟΥΠΟΘΕΣΗ ΟΤΙ Ο ΣΤΑΘΕΡΟΣ ΟΡΟΣ ΕΙΝΑΙ ΟΠΩΣ ΤΟΝ ΕΧΩ ΓΡΑΨΕΙ ΕΓΩ)

Τεσπα δούλεψε με τη διακρίνουσα και θα πάρεις ότι α^2+β^2+γ^2=αβ+βγ+γα το οποίο ισχύει μόνο όταν α=β=γ. Το γιατί το αφήνω να το βρεις μόνος σου

miv · 14-02-09

Πήγαινε με το ευθύ πρώτα, θεωρώντας ότι α=β=γ. Από τη θεωρία είναι γνωστό πως ένα τριώνυμο στο R έχει διπλή ρίζα αν Δ=0. Οπότε αφού θεωρείς α=β=γ προσπαθείς να αποδείξεις ότι Δ=0.
Η έκφραση ΑΝ ΚΑΙ ΜΟΝΟ ΑΝ αυτομάτως σου λέει ότι οφείλεις να αποδείξεις και το αντίστροφο. Έστω, λοιπόν, ότι το τριώνυμο έχει διπλή ρίζα, δηλαδή έστω Δ=0. Και με δεδομένο αυτό, θα δείξεις ότι α=β=γ.

djimmakos · 14-02-09

Αρχική Δημοσίευση από miv:
Πήγαινε με το ευθύ πρώτα, θεωρώντας ότι α=β=γ. Από τη θεωρία είναι γνωστό πως ένα τριώνυμο στο R έχει διπλή ρίζα αν Δ=0. Οπότε αφού θεωρείς α=β=γ προσπαθείς να αποδείξεις ότι Δ=0.
Η έκφραση ΑΝ ΚΑΙ ΜΟΝΟ ΑΝ αυτομάτως σου λέει ότι οφείλεις να αποδείξεις και το αντίστροφο. Έστω, λοιπόν, ότι το τριώνυμο έχει διπλή ρίζα, δηλαδή έστω Δ=0. Και με δεδομένο αυτό, θα δείξεις ότι α=β=γ.

Ωχ αυτό το είχα ξεχάσει τελείως...

Ναι σαι καλά ρε μιβ που μου το θύμησες

Θα γράψω τη λύση ολοκληρωμένη και θα την ανεβάσω κάποια στιγμή

miv · 14-02-09

Αυτό το καλύπτεις αν αποδείξεις το ευθύ και διατηρήσεις με βεβαιότητα τις ισοδυναμίες, αλλά είναι πιο ασφαλές αν τα αποδείξεις ξεχωριστά.

djimmakos · 14-02-09

Αρχική Δημοσίευση από miv:
Αυτό το καλύπτεις αν αποδείξεις το ευθύ και διατηρήσεις με βεβαιότητα τις ισοδυναμίες, αλλά είναι πιο ασφαλές αν τα αποδείξεις ξεχωριστά.

Εγώ πήρα τη διακρίνουσα ίση με 0 και έφτασα στο συμπέρασμα ότι για να είναι μηδέν πρέπει:

α^2+β^2+γ^2=αβ+βγ+γα το οποίο ισχύει αν και μόνο αν α=β=γ

miv · 14-02-09

Αυτό ισχύει από κάποια θεωρία ή το λες επειδή βγαίνει αν κάνεις δοκιμή; Δεν θυμάμαι να το έχω δει αυτό, εκτός κι αν θυμάμαι λάθος.
Εκτός κι αν τα φέρεις όλα μπροστά και με παραγοντοποιήσεις και πράξεις αποδείξεις τον ισχυρισμό σου, αλλά δεν σου εγγυώμαι ότι θα βγει με τη μία.

djimmakos · 14-02-09

Αρχική Δημοσίευση από miv:
Αυτό ισχύει από κάποια θεωρία ή το λες επειδή βγαίνει αν κάνεις δοκιμή; Δεν θυμάμαι να το έχω δει αυτό, εκτός κι αν θυμάμαι λάθος.
Εκτός κι αν τα φέρεις όλα μπροστά και με παραγοντοποιήσεις και πράξεις αποδείξεις τον ισχυρισμό σου, αλλά δεν σου εγγυώμαι ότι θα βγει με τη μία.

Το έχω αποδείξει..

Boom · 14-02-09

με τν εκφραση ΑΝ ΚΑΙ ΜΟΝΟ ΑΝ αρκει να αποδειξεις οτι ισχυει μονο το ενα αλλα να βαλεις διπλο συνεπαγεται...

βιλλαρασ · 14-02-09

Αρχική Δημοσίευση από Djimmakos:
Εγώ πήρα τη διακρίνουσα ίση με 0 και έφτασα στο συμπέρασμα ότι για να είναι μηδέν πρέπει:

α^2+β^2+γ^2=αβ+βγ+γα το οποίο ισχύει αν και μόνο αν α=β=γ

και εγω εκει κατεληξα αλλα δεν φερω καμια τετια ταυτοτητα που να βοηθαει

djimmakos · 14-02-09

Γράφω τη λύση όπως είπε ο miv:

Έχουμε την εξίσωση:

$3x^2+2(a+b+c)x+(ab+bc+ca)=0$

Θα δείξουμε ότι αν a=b=c τότε έχει διπλή ρίζα και ότι αν έχει διπλή ρίζα τότε a=b=c.

Λοιπόν

Έστω ότι a=b=c

Τότε η εξίσωση γίνεται:

$3x^2+6ax+3a^2 (i)$

και επειδή η διακρίνουσα της (i) είναι ίση με το 0, η αρχική εξίσωση έχει μια διπλή ρίζα

Έστω τώρα ότι η αρχική εξίσωση έχει διπλή ρίζα. Θα αποδείξουμε ότι a=b=c

Για να έχει η αρχική εξίσωση μια διπλή ρίζα πρέπει η διακρίνουσα της να είναι ίση με το 0. Δηλαδή:

$\Delta =0 \Leftrightarrow [2(a+b+c)]^2-12(ab+bc+ca)=0\Leftrightarrow 4(a^2+b^2+c^2+2ab+2bc+2ac)-12(ab+bc+ca)=0\Leftrightarrow (a^2+b^2+c^2+2ab+2bc+2ac)-3(ab+bc+ca)=0\Leftrightarrow a^2+b^2+c^2-ab-bc-ca=0\Leftrightarrow a^2+b^2+c^2=ab+bc+ca (ii)$

Tώρα αρκεί να δείξουμε ότι η (ii) ισχύει όταν a=b=c.

Έχουμε:

$a^2+b^2+c^2=ab+bc+ca\Leftrightarrow 2a^2+2b^2+2c^2=2ab+2ac+2bc\Leftrightarrow a^2+a^2+b^2+b^2+c^2+c^2=2ab+2ac+2bc\Leftrightarrow (a^2-2ab+b^2)+(a^2-2ac+c^2)+(b^2-2bc+c^2)=0 \Leftrightarrow (a-b)^2+(a-c)^2 + (b-c)^2=0 (iii)$

Για να ισχύει η (iii) πρέπει:

$a-b=0 \Leftrightarrow a=b$
$a-c=0\Leftrightarrow a=c$
$b-c=0 \Leftrightarrow b=c$

δηλαδή a=b=c

Και έτσι τελειώσαμε...

Αν δείτε κανά λάθος πείτε...
Άνθρωπος είμαι

Boom · 11 Ιουλίου 2012

Αρχική Δημοσίευση από Djimmakos:
Γράφω τη λύση όπως είπε ο miv:

Έχουμε την εξίσωση:

$3x^2+2(a+b+c)x+(ab+bc+ca)=0$

Θα δείξουμε ότι αν a=b=c τότε έχει διπλή ρίζα και ότι αν έχει διπλή ρίζα τότε a=b=c.

Λοιπόν

Έστω ότι a=b=c

Τότε η εξίσωση γίνεται:

$3x^2+6ax+3a^2 (i)$

και επειδή η διακρίνουσα της (i) είναι ίση με το 0, η αρχική εξίσωση έχει μια διπλή ρίζα

Έστω τώρα ότι η αρχική εξίσωση έχει διπλή ρίζα. Θα αποδείξουμε ότι a=b=c

Για να έχει η αρχική εξίσωση μια διπλή ρίζα πρέπει η διακρίνουσα της να είναι ίση με το 0. Δηλαδή:

$Delta =0 Leftrightarrow [2(a+b+c)]^2-12(ab+bc+ca)=0Leftrightarrow 4(a^2+b^2+c^2+2ab+2bc+2ac)-12(ab+bc+ca)=0Leftrightarrow (a^2+b^2+c^2+2ab+2bc+2ac)-3(ab+bc+ca)=0Leftrightarrow a^2+b^2+c^2-ab-bc-ca=0Leftrightarrow a^2+b^2+c^2=ab+bc+ca (ii)$

Tώρα αρκεί να δείξουμε ότι η (ii) ισχύει όταν a=b=c.

Έχουμε:

$a^2+b^2+c^2=ab+bc+caLeftrightarrow 2a^2+2b^2+2c^2=2ab+2ac+2bcLeftrightarrow a^2+a^2+b^2+b^2+c^2+c^2=2ab+2ac+2bcLeftrightarrow (a^2-2ab+b^2)+(a^2-2ac+c^2)+(b^2-2bc+c^2)=0 Leftrightarrow (a-b)^2+(a-c)^2 + (b-c)^2=0 (iii)$

Για να ισχύει η (iii) πρέπει:

$a-b=0 Leftrightarrow a=b$
$a-c=0Leftrightarrow a=c$
$b-c=0 Leftrightarrow b=c$

δηλαδή a=b=c

Και έτσι τελειώσαμε...

Αν δείτε κανά λάθος πείτε...
Άνθρωπος είμαι

:!:

djimmakos · 14-02-09

Γελάσαμε Δώρα:p

Βοήθεια/Απορίες στην Άλγεβρα

Διάσημο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένο μέλος

Διάσημο μέλος

Πολύ δραστήριο μέλος

Περιβόητο μέλος

Διάσημο μέλος

Εκκολαπτόμενο μέλος

Διάσημο μέλος

Επιφανές μέλος

Διάσημο μέλος

Επιφανές μέλος

Διάσημο μέλος

Επιφανές μέλος

Διάσημο μέλος

Επιφανές μέλος

Εκκολαπτόμενο μέλος

Διάσημο μέλος

Επιφανές μέλος

Διάσημο μέλος