Βοήθεια/Απορίες στα Μαθηματικά Προσανατολισμού - Θεωρία

[coheNakatos]

Σας παρακαλώ ειναι μεγαλη αναγκη πως το παραγωγίζω?Είναι σταθερά???

Το μηνυμα σου με latex

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Eli4s]

αφού το ορισμένο ολοκλήρωμα είναι πραγματικος αριθμός δν θα ναι μηδεν?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mina14]

Αυτο νομιζω αλλα θα θελα επιβεβαιωση!!!

Ευχαριστώ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Eli4s]

να παραθέσω κ εγώ κατι: Να βρεθούν 2 αριθμοί α, β πραγματικοί, θετικοί, μη μηδενικοί και διάφοροι του 2 τέτοιοι ώστε:

α+β=α*β


βασικά ειναι λίγο εκτος (γιατί είναι θεωρία αριθμών) απλά είναι ενδιαφέρον..​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Dias]

Να βρεθούν 2 αριθμοί α, β πραγματικοί, θετικοί, μη μηδενικοί και διάφοροι του 2 τέτοιοι ώστε: α+β=α*β

Να κάνω μια προσπάθεια?
α+β = α.β = κ με κ>0 και κ διάφορο 4. Τα α, β λύσεις εξίσωσης: χ²-κχ+κ = 0. Δ = κ²-4κ > 0 ==> κ>4.
Άρα: α = [κ+V(κ²-4κ)]/2 και β = [κ-V(κ²-4κ)]/2 με κ>4. (V ρίζα)

​

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[coheNakatos]

αφού το ορισμένο ολοκλήρωμα είναι πραγματικος αριθμός δν θα ναι μηδεν?

Οχι παιδια λαθος ! πρεπει να αλλαξεις το εσωτερικο ! Θεσε k=t-x και θα δεις οτι θα αλλαξουν τα ακρα !

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Eli4s]

Να κάνω μια προσπάθεια?
α+β = α.β = κ με κ>0 και κ διάφορο 4. Τα α, β λύσεις εξίσωσης: χ²-κχ+κ = 0. Δ = κ²-4κ > 0 ==> κ>4.
Άρα: α = [κ+V(κ²-4κ)]/2 και β = [κ-V(κ²-4κ)]/2 με κ>4. (V ρίζα)

​

Συμφωνώ και στελνω pm για γενικότερη λύση.. Όμως είναι λίγο πιο δύσκολο αν αντί για πραγματικούς αναζητήσουμε λύσεις σε ακεραίους..!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[metalmaniac]

Αν f(k) είναι ακρότατο τη f να βρείτε το εμβαδόν που ορίζεται αποτην cf την εφαπτομένη της f στο (k,f(k))και τις ευθείες χ=κ,χ=e Δινεται f(x)=1+x-(lnx?x)

Να βρείτε το εμβαδον που ορίζετα απο τις f(x)=x-1(όλο σε ρίζα) και g(x)=(x+1)/3 και τον χ'χ.Μου βγαίνει αρνητικό εμαβδον και δεν μπορώ να βρώ το λάθος.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[sjpapa]

Ενα παραδειγμα:
f(x) = 1, για χ != χ0, f(x0)= 2

οποτε ειναι λαθος

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[lowbaper92]

Ένα σωστό-λάθος για μαθητές.

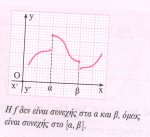
Άν η f δεν είναι συνεχής στα α και β , τότε δεν είναι συνεχής και στο [α,β]

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Μέγα-Μπιπ]

Ένα σωστό-λάθος για μαθητές.

Άν η f δεν είναι συνεχής στα α και β , τότε δεν είναι συνεχής και στο [α,β]

Είναι σωστό διότι ο ορισμός λέει ότι μία συνάρτηση f είναι συνεχής σε κλειστό διάστημα [α,β] όταν είναι συνεχής σε κάθε σημείο του (α,β) ΚΑΙ στα σημεία α και β!!!αφού λοιπόν δεν είναι συνεχής στα δύο σημεία δεν είναι σ'όλο το διάστημα [α,β]!!!!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Μέγα-Μπιπ]

Αν f(k) είναι ακρότατο τη f να βρείτε το εμβαδόν που ορίζεται αποτην cf την εφαπτομένη της f στο (k,f(k))και τις ευθείες χ=κ,χ=e Δινεται f(x)=1+x-(lnx?x)

Να βρείτε το εμβαδον που ορίζετα απο τις f(x)=x-1(όλο σε ρίζα) και g(x)=(x+1)/3 και τον χ'χ.Μου βγαίνει αρνητικό εμαβδον και δεν μπορώ να βρώ το λάθος.

Νόμιζω ότι πρέπει να σιγουρευτείς ότι έχεις βάλει απόλυτο(εκτός αν έχεις ήδη βρεί ποία συνάρτηση είναι μεγαλύτερη)!!!!γιατί αν έχεις βάλει δεν μπορεί να σου βγαίνει αρνητικό εμβαδό!!!!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[coheNakatos]

Ένα σωστό-λάθος για μαθητές.

Άν η f δεν είναι συνεχής στα α και β , τότε δεν είναι συνεχής και στο [α,β]

Εγω λεω οτι ειναι λαθος , γιατι ο ορισμος δεν λεει να ειναι συνεχης στα α,β αλλα τα πλευρικα ορια να ειναι ισα με τις τιμες

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[lowbaper92]

Είναι σωστό διότι ο ορισμός λέει ότι μία συνάρτηση f είναι συνεχής σε κλειστό διάστημα [α,β] όταν είναι συνεχής σε κάθε σημείο του (α,β) ΚΑΙ στα σημεία α και β!!!αφού λοιπόν δεν είναι συνεχής στα δύο σημεία δεν είναι σ'όλο το διάστημα [α,β]!!!!

Βασικά ο ορισμός δεν λέει αυτο !

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[lowbaper92]

Για δείτε εδώ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[coheNakatos]

Για δείτε εδώ

Και εγω αυτο ειπα ρε lowbaper λαθος ειπα και δικαιολογησα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Μέγα-Μπιπ]

Παιδιά στις εξετάσεις του 2008 και τις επαναληπτικές του 2004 ζητήθηκε το ερώτημα:

Πότε μία συνάρτηση είναι συνεχής σε ένα κλειστό διάστημα [α,β]
Η απάντηση είναι στο σχολικό βιβλίο στη σελίδα 191!!!!!Και θα καταλάβετε ότι είναι σωστή η πρόταση!!!!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[coheNakatos]

Παιδιά στις εξετάσεις του 2008 και τις επαναληπτικές του 2004 ζητήθηκε το ερώτημα:

Πότε μία συνάρτηση είναι συνεχής σε ένα κλειστό διάστημα [α,β]
Η απάντηση είναι στο σχολικό βιβλίο στη σελίδα 191!!!!!Και θα καταλάβετε ότι είναι σωστή η πρόταση!!!!

Σου απαντησαμε 2 φορες δεν λεει αυτο

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Μέγα-Μπιπ]

Σου απαντησαμε 2 φορες δεν λεει αυτο

στην σελιδα 191 του σχολικού βιβλίου δεν λέει ότι:Μία f είναι συνεχής σ'ένα κλειστό διάστημα [α,β] όταν ισχύει ότι είναι συνεχής σε κάθε σημείο του (α,β) και επιπλέον ισχύει ότι limf(x)(x-->a)=f(a) και limf(x)(x-->β)=f(β)



δεν τ λέει αυτό κάπου????????

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[coheNakatos]

στην σελιδα 191 του σχολικού βιβλίου δεν λέει ότι:Μία f είναι συνεχής σ'ένα κλειστό διάστημα [α,β] όταν ισχύει ότι είναι συνεχής σε κάθε σημείο του (α,β) και επιπλέον ισχύει ότι limf(x)(x-->a)=f(a) και limf(x)(x-->β)=f(β)



δεν τ λέει αυτό κάπου????????

Εδω υπαρχει η λεπτομερεια που κανει την διαφορα λεει και

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 14 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.