paganini666
Δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Αν η f είναι συνεχής στο [α,β], παραγωγίσιμη στο (α,β) και f(α)=f(β)=0, τότε να αποδειχθεί ότι υπάρχει
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
m3Lt3D
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
andreas157
Εκκολαπτόμενο μέλος


έστω ότι έχω μια διανυσματική συνάρτηση του t πχ
r(t) = x(t)xo + y(t)yo
τι κάνω για να βρώ την φυσική παραμετρική εξίσωση
r(s) = x(s)xo + y(s)yo ?
αν γίνεται βάλτε και ένα παράδειγμα για να καταλάβω...
όπου bold διανύσματα...
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


να ρωτήσω και εγώ κάτι?
έστω ότι έχω μια διανυσματική συνάρτηση του t πχ
r(t) = x(t)xo + y(t)yo
τι κάνω για να βρώ την φυσική παραμετρική εξίσωση
r(s) = x(s)xo + y(s)yo ?
αν γίνεται βάλτε και ένα παράδειγμα για να καταλάβω...
όπου bold διανύσματα...
Είναι μια διαδικασία που δεν είναι πάντα εφικτή. Πρώτα απ' όλα επιλέγεις αυθαίρετα ένα σημείο της καμπύλης C
Το πεδίο ορισμού
Τότε η εξίσωση της καμπύλης γίνεται:
Άρα
Αν μπορούμε να προσδιορίσουμε την αντίστροφη της f, τότε μπορεί να γραφεί η C στη μορφή
-----------------------------------------
Ας εξετάσουμε για παράδειγμα τον κύκλο κέντρου Ο(0,0) και ακτίνας ρ. Ως γνωστόν η εξίσωσή του στο επίπεδο Οxy είναι C:
Οι παραμετρικές εξισώσεις του κύκλου αυτού είναι
όπου
Ας θεωρήσουμε ως αρχή του συστήματος καμπυλόγραμμων συντεταγμένων το σημείο του κύκλου που αντιστοιχεί στην τιμή
οπότε η αρχή είναι το σημείο
Η φ θεωρείται θετική όταν διαγράφεται δεξιόστροφα. Όταν η φ είναι θετιή τότε και η s είναι θετική.
Καταλήξαμε στη γνωστή σχέση s=ρφ από την Ευκλείδεια Γεωμετρία.
Η f έχει πεδίο ορισμού
όπου
Αντικαθιστώντας στις αρχικές παραμετρικές εξισώσεις προκύπτει:
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
andreas157
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


https://www.mathematica.gr/forum/viewtopic.php?f=51&t=1861&p=10639#p10639Δεν κάνει τίποτα Ανδρέα.
θυμασαι εκεινο το προβλημα; δες εδω ποικιλια λυσεων!!!
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


https://www.mathematica.gr/forum/viewtopic.php?f=51&t=1861&p=10639#p10639
θυμασαι εκεινο το προβλημα; δες εδω ποικιλια λυσεων!!!
Ο Χριστός και η Παναγία. Η δική μου η λύση ήταν πιο απλή στην σκέψη αν και μπελαλίδικη και αυτή στις πράξεις.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Να βρείτε τον τύπο της f όταν για οποιουσδήποτε πραγματικούς αριθμούς x,y ισχύει, f(0)=0
Λάθος λύση. Την έσβησα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


ωραια δημοσιευσε τη λυση σου εδω https://www.mathematica.gr/forum/viewtopic.php?f=52&t=1885Βρήκα μια λύση χωρίς να μου χρειαστεί το f(0)=0.
Κατ' αρχήν πρέπειγια κάθε
ώστε η ρίζα να έχει νόημα. Τότε η ισότητα γράφεται ισοδύναμα:
για κάθε
Θέτω y=-1:
για κάθε
Όμως. Επομένως πρέπει να ισχύει
Άραγια κάθε
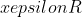
 και πες τους το!
και πες τους το!Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
galois01
Νεοφερμένο μέλος


Να βρείτε τον τύπο της f όταν για οποιουσδήποτε πραγματικούς αριθμούς x,y ισχύει, f(0)=0
Πρέπει
Για x=y=0 η υπόθεση μας δίνει
Για y=-x έχουμε
Επομένως
Αρχική Δημοσίευση από Civilara:Να βρεθεί η εφαπτομένη της επίπεδης καμπύλης C:στο σημείο της M(1,0)
Παραγωγίζουμε και τα δύο μέλη της εξίσωσης της καμπύλης ως προς χ και έχουμε
Στο σημείο Μ(1,0) της καμπύλης ο συντελεστής διεύθυνσης είναι
Βλέπουμε πως για το σημείο Μ(1,0) δεν ορίζεται συντελεστής διεύθυνσης.
Επομένως η καμπύλη στο σήμειο Μ(1,0) έχει κατακόρυφη εφαπτομένη την
Ελπίζω να μην υπάρχει κάποιο λάθος.
Κώστας

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Αν και βγαίνει και πιο σύντομα, σωστός:no1:. Για μαθητής Γ' Λυκείου είσαι πάρα πολύ καλός
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
galois01
Νεοφερμένο μέλος


Αν και βγαίνει και πιο σύντομα, σωστός:no1:
Μπορείς μήπως να γράψεις τη λύση σου?
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
paganini666
Δραστήριο μέλος


 ) θελω να μαθω για αυτα τα επικαμπυλια ολοκληρωματα,τα τριπλα και γιααυτο το συμβολο που μοιαζει με ολοκληρωμα αλλα εχει μια μπαλα στη μεση. Pleaseeeee! Βαλε μερικες πολυ πολυ απλες εφαρμογες να καταλαβω.
) θελω να μαθω για αυτα τα επικαμπυλια ολοκληρωματα,τα τριπλα και γιααυτο το συμβολο που μοιαζει με ολοκληρωμα αλλα εχει μια μπαλα στη μεση. Pleaseeeee! Βαλε μερικες πολυ πολυ απλες εφαρμογες να καταλαβω.Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
galois01
Νεοφερμένο μέλος


γιααυτο το συμβολο που μοιαζει με ολοκληρωμα αλλα εχει μια μπαλα στη μεση.
Αν δεν κάνω λάθος έτσι συμβολίζουμε τα επικαμπύλια ολοκληρώματα.
Κώστας
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


ρε συ σιφιλιαρα () θελω να μαθω για αυτα τα επικαμπυλια ολοκληρωματα,τα τριπλα και γιααυτο το συμβολο που μοιαζει με ολοκληρωμα αλλα εχει μια μπαλα στη μεση. Pleaseeeee! Βαλε μερικες πολυ πολυ απλες εφαρμογες να καταλαβω.
 Ωραίος ρε μάγκα. Με πέθανες. Τι σε ενδιαφέρουν αυτά όμως ρε Ηλία, αφού ιατρική θες να πας.
Ωραίος ρε μάγκα. Με πέθανες. Τι σε ενδιαφέρουν αυτά όμως ρε Ηλία, αφού ιατρική θες να πας.Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

